Ken Shirriff's blog

Computer history, restoring vintage computers, IC reverse engineering, and whatever

Bitcoin mining on a 55 year old IBM 1401 mainframe: 80 seconds per hash

Could an IBM mainframe from the 1960s mine Bitcoin? The idea seemed crazy, so I decided to find out. I implemented the Bitcoin hash algorithm in assembly code for the IBM 1401 and tested it on a working vintage mainframe. It turns out that this computer could mine, but so slowly it would take more than the lifetime of the universe to successfully mine a block. While modern hardware can compute billions of hashes per second, the 1401 takes 80 seconds to compute a single hash. This illustrates the improvement of computer performance in the past decades, most famously described by Moore's Law. The photo below shows the card deck I used, along with the output of my SHA-256 hash program as printed by the line printer. (The card on the front of the deck is just for decoration; it was a huge pain to punch.) Note that the second line of output ends with a bunch of zeros; this indicates a successful hash.

Card deck used to compute SHA-256 hashes on IBM 1401 mainframe. Behind the card deck is the line printer output showing the input to the algorithm and the resulting hash.

How Bitcoin mining works

Bitcoin, a digital currency that can be transmitted across the Internet, has attracted a lot of attention lately. If you're not familiar with how it works, the Bitcoin system can be thought of as a ledger that keeps track of who owns which bitcoins, and allows them to be transferred from one person to another. The interesting thing about Bitcoin is there's no central machine or authority keeping track of things. Instead, the records are spread across thousands of machines on the Internet. The difficult problem with a distributed system like this is how to ensure everyone agrees on the records, so everyone agrees if a transaction is valid, even in the presence of malicious users and slow networks. The solution in Bitcoin is a process called mining—about every 10 minutes a block of outstanding transactions is mined, which makes the block official. To prevent anyone from controlling which transactions are mined, the mining process is very difficult and competitive. In particular a key idea of Bitcoin is that mining is made very, very difficult, a technique called proof-of-work. It takes an insanely huge amount of computational effort to mine a block, but once a block has been mined, it is easy for peers on the network to verify that a block has been successfully mined. The difficulty of mining keeps anyone from maliciously taking over Bitcoin, and the ease of checking that a block has been mined lets users know which transactions are official. As a side-effect, mining adds new bitcoins to the system. For each block mined, miners currently get 25 new bitcoins (currently worth about $6,000), which encourages miners to do the hard work of mining blocks. With the possibility of receiving $6,000 every 10 minutes, there is a lot of money in mining and people invest huge sums in mining hardware.

Line printer, IBM 1401 mainframe, and tape drives at the Computer History Museum.

Line printer and IBM 1401 mainframe at the Computer History Museum. This is the computer I used to run my program. The console is in the upper left. Each of the dark rectangular panels on the computer is a "gate" that can be folded out for maintenance. Mining requires a task that is very difficult to perform, but easy to verify. Bitcoin mining uses cryptography, with a hash function called double SHA-256. A hash takes a chunk of data as input and shrinks it down into a smaller hash value (in this case 256 bits). With a cryptographic hash, there's no way to get a hash value you want without trying a whole lot of inputs. But once you find an input that gives the value you want, it's easy for anyone to verify the hash. Thus, cryptographic hashing becomes a good way to implement the Bitcoin "proof-of-work". In more detail, to mine a block, you first collect the new transactions into a block. Then you hash the block to form an (effectively random) block hash value. If the hash starts with 16 zeros, the block is successfully mined and is sent into the Bitcoin network. Most of the time the hash isn't successful, so you modify the block slightly and try again, over and over billions of times. About every 10 minutes someone will successfully mine a block, and the process starts over. It's kind of like a lottery, where miners keep trying until someone "wins". It's hard to visualize just how difficult the hashing process is: finding a valid hash is less likely than finding a single grain of sand out of all the sand on Earth. To find these hashes, miners have datacenters full of specialized hardware to do this mining. I've simplified a lot of details. For in-depth information on Bitcoin and mining, see my articles Bitcoins the hard way and Bitcoin mining the hard way.

The SHA-256 hash algorithm used by Bitcoin

Next, I'll discuss the hash function used in Bitcoin, which is based on a standard cryptographic hash function called SHA-256. Bitcoin uses "double SHA-256" which simply applies the SHA-256 function twice. The SHA-256 algorithm is so simple you can literally do it by hand, but it manages to scramble the data entirely unpredictably. The algorithm takes input blocks of 64 bytes, combines the data cryptographically, and generates a 256-bit (32 byte) output. The algorithm uses a simple round and repeats it 64 times. The diagram below shows one round, which takes eight 4-byte inputs, A through H, performs a few operations, and generates new values for A through H.

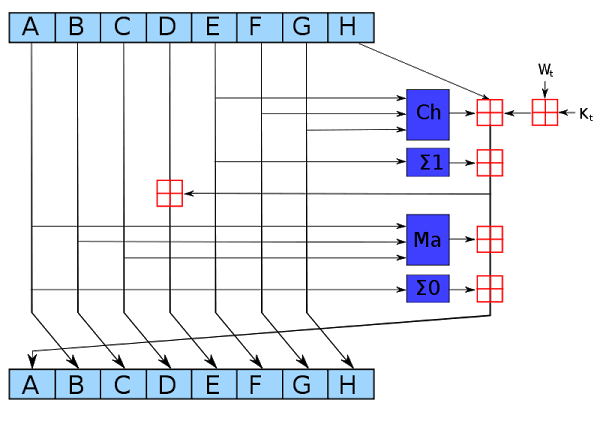SHA-256 round, from Wikipedia created by kockmeyer, CC BY-SA 3.0. The dark blue boxes mix up the values in non-linear ways that are hard to analyze cryptographically. (If you could figure out a mathematical shortcut to generate successful hashes, you could take over Bitcoin mining.) The Ch"choose" box chooses bits from F or G, based on the value of input E. The Σ "sum" boxes rotate the bits of A (or E) to form three rotated versions, and then sums them together modulo 2. The Ma"majority" box looks at the bits in each position of A, B, and C, and selects 0 or 1, whichever value is in the majority. The red boxes perform 32-bit addition, generating new values for A and E. The input W_tis based on the input data, slightly processed. (This is where the input block gets fed into the algorithm.) The input K_tis a constant defined for each round. As can be seen from the diagram above, only A and E are changed in a round. The other values pass through unchanged, with the old A value becoming the new B value, the old B value becoming the new C value and so forth. Although each round of SHA-256 doesn't change the data much, after 64 rounds the input data will be completely scrambled, generating the unpredictable hash output.

The IBM 1401

I decided to implement this algorithm on the IBM 1401 mainframe. This computer was announced in 1959, and went on to become the best-selling computer of the mid-1960s, with more than 10,000 systems in use. The 1401 wasn't a very powerful computer even for 1960, but since it leased for the low price of $2500 a month, it made computing possible for mid-sized businesses that previously couldn't have afforded a computer. The IBM 1401 didn't use silicon chips. In fact it didn't even use silicon. Its transistors were built out of a semiconductor called germanium, which was used before silicon took over. The transistors and other components were mounted on boards the size of playing cards called SMS cards. The computer used thousands of these cards, which were installed in racks called "gates". The IBM 1401 had a couple dozen of these gates, which folded out of the computer for maintenance. Below, one of the gates is opened up showing the circuit boards and cabling.

Cards and wires inside an IBM 1401 mainframe.

This shows a rack (called a "gate") folded out of the IBM 1401 mainframe. The photo shows the SMS cards used to implement the circuits. This specific rack controls the tape drives. Internally, the computer was very different from modern computers. It didn't use 8-bit bytes, but 6-bit characters based on binary coded decimal (BCD). Since it was a business machine, the computer used decimal arithmetic instead of binary arithmetic and each character of storage held a digit, 0 through 9. The computer came with 4000 characters of storage in magnetic core memory; a dishwasher-sized memory expansion box provided 12,000 more characters of storage. The computer was designed to use punched cards as input, with a card reader that read the program and data. Output was printed on a fast line printer or could be punched on more cards. The Computer History Museum in Mountain View has two working IBM 1401 mainframes. I used one of them to run the SHA-256 hash code. For more information on the IBM 1401, see my article Fractals on the IBM 1401.

Implementing SHA-256 on the IBM 1401

The IBM 1401 is almost the worst machine you could pick to implement the SHA-256 hash algorithm. The algorithm is designed to be implemented efficiently on machines that can do bit operations on 32-bit words. Unfortunately, the IBM 1401 doesn't have 32-bit words or even bytes. It uses 6-bit characters and doesn't provide bit operations. It doesn't even handle binary arithmetic, using decimal arithmetic instead. Thus, implementing the algorithm on the 1401 is slow and inconvenient. I ended up using one character per bit. A 32-bit value is stored as 32 characters, either "0" or "1". My code has to perform the bit operations and additions character-by-character, basically checking each character and deciding what to do with it. As you might expect, the resulting code is very slow. The assembly code I wrote is below. The comments should give you a rough idea of how the code works. Near the end of the code, you can see the table of constants required by the SHA-256 algorithm, specified in hex. Since the 1401 doesn't support hex, I had to write my own routines to convert between hex and binary. I won't try to explain IBM 1401 assembly code here, except to point out that it is very different from modern computers. It doesn't even have subroutine calls and returns. Operations happen on memory, as there aren't any general-purpose registers.

               job  bitcoin
     * SHA-256 hash
     * Ken Shirriff  //righto.com
               ctl  6641

               org  087
     X1        dcw  @000@
               org  092
     X2        dcw  @000@
               org  097
     X3        dcw  @000@
     
               org  333
     start     cs   299
               r
               sw   001
               lca  064, input0
               mcw  064, 264
               w
     * Initialize word marks on storage
               mcw  +s0, x3

     wmloop    sw   0&x3  
               ma   @032@, x3
               c    +h7+32, x3
               bu   wmloop
     
               mcw  +input-127, x3      * Put input into warr[0] to warr[15]
               mcw  +warr, x1
               mcw  @128@, tobinc
               b    tobin
     
     * Compute message schedule array w[0..63]
  
               mcw  @16@, i
     * i is word index 16-63   
     * x1 is start of warr[i-16], i.e. bit 0 (bit 0 on left, bit 31 on right)   
               mcw  +warr, x1
     wloop     c    @64@, i
               be   wloopd
     
     * Compute s0
               mcw  +s0, x2
               za   +0, 31&x2               * Zero s0
     * Add w[i-15] rightrotate 7
               sw   7&x2               * Wordmark at bit 7 (from left) of s0
               a    56&x1, 31&x2       * Right shifted: 32+31-7 = bit 24 of w[i-15], 31 = end of s0
               a    63&x1, 6&x2        * Wrapped: 32+31 = end of w[i-15], 7-1 = bit 6 of s0   
               cw   7&x2               * Clear wordmark
     * Add w[i-15] rightrotate 18
               sw   18&x2              * Wordmark at bit 18 (from left) of s0
               a    45&x1, 31&x2       * Right shifted: 32+31-18 = bit 13 of w[i-15], 31 = end of s0
               a    63&x1, 17&x2       * Wrapped: 32+31 = end of w[i-15], 18-1 = bit 17 of s0   
               cw   18&x2              * Clear wordmark
     * Add w[i-15] rightshift 3
               sw   3&x2               * Wordmark at bit 3 (from left) of s0
               a    60&x1, 31&x2       * Right shifted: 32+31-3 = bit 28 of w[i-15], 31 = end of s0
               cw   3&x2               * Clear wordmark
     * Convert sum to xor
               mcw  x1, x1tmp
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s0                 * Restore wordmark cleared by xor
     
               mcw  x1tmp, x1
     
     * Compute s1         
               mcw  +s1, x2
               za   +0, 31&x2               * Zero s1
     * Add w[i-2] rightrotate 17
               sw   17&x2              * Wordmark at bit 17 (from left) of s1
               a    462&x1, 31&x2      * Right shifted: 14*32+31-17 = bit 14 of w[i-2], 31 = end of s1
               a    479&x1, 16&x2      * Wrapped: 14*32+31 = end of w[i-2], 17-1 = bit 16 of s1   
               cw   17&x2              * Clear wordmark
     * Add w[i-2] rightrotate 19
               sw   19&x2              * Wordmark at bit 19 (from left) of s1
               a    460&x1, 31&x2      * Right shifted: 14*32+31-19 = bit 12 of w[i-2], 31 = end of s1
               a    479&x1, 18&x2      * Wrapped: 14*32+31 = end of w[i-2], 19-1 = bit 18 of s1  
               cw   19&x2              * Clear wordmark
     * Add w[i-2] rightshift 10
               sw   10&x2              * Wordmark at bit 10 (from left) of s1
               a    469&x1, 31&x2      * Right shifted: 14*32+31-10 = bit 21 of w[i-2], 31 = end of s1
               cw   10&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s1+31, x1         * x1 = right end of s1
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s1                 * Restore wordmark cleared by xor
     
     * Compute w[i] := w[i-16] + s0 + w[i-7] + s1
               mcw  x1tmp, x1
               a    s1+31, s0+31       * Add s1 to s0
               a    31&x1, s0+31       * Add w[i-16] to s0
               a    319&x1, s0+31      * Add 9*32+31 = w[i-7] to s0
     * Convert bit sum to 32-bit sum
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    sum
               sw   s0                 * Restore wordmark cleared by sum
     

     
               mcw  x1tmp, x1
               mcw  s0+31, 543&x1      * Move s0 to w[i]
       
              
               ma   @032@, x1
               a    +1, i
               mz   @0@, i
               b    wloop
     
     x1tmp     dcw  #5
     

     * Initialize: Copy hex h0init-h7init into binary h0-h7
     wloopd    mcw  +h0init-7, x3
               mcw  +h0, x1
               mcw  @064@, tobinc       * 8*8 hex digits
               b    tobin
     
     
     * Initialize a-h from h0-h7
               mcw  @000@, x1
     ilp       mcw  h0+31&x1, a+31&x1
               ma   @032@, x1
               c    x1, @256@
               bu   ilp
     
               mcw  @000@, bitidx      * bitidx = i*32 = bit index
               mcw  @000@, kidx        * kidx = i*8 = key index
                

     * Compute s1 from e        
     mainlp    mcw  +e, x1
               mcw  +s1, x2
               za   +0, 31&x2               * Zero s1
     * Add e rightrotate 6
               sw   6&x2               * Wordmark at bit 6 (from left) of s1
               a    25&x1, 31&x2       * Right shifted: 31-6 = bit 25 of e, 31 = end of s1
               a    31&x1, 5&x2        * Wrapped: 31 = end of e, 6-1 = bit 5 of s1   
               cw   6&x2               * Clear wordmark
     * Add e rightrotate 11
               sw   11&x2              * Wordmark at bit 11 (from left) of s1
               a    20&x1, 31&x2       * Right shifted: 31-11 = bit 20 of e, 31 = end of s1
               a    31&x1, 10&x2       * Wrapped: 31 = end of e, 11-1 = bit 10 of s1   
               cw   11&x2              * Clear wordmark
     * Add e rightrotate 25
               sw   25&x2              * Wordmark at bit 25 (from left) of s1
               a    6&x1, 31&x2        * Right shifted: 31-25 = bit 6 of e, 31 = end of s1
               a    31&x1, 24&x2       * Wrapped: 31 = end of e, 25-1 = bit 24 of s1   
               cw   25&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s1+31, x1         * x1 = right end of s1
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s1                 * Restore wordmark cleared by xor

     * Compute ch: choose function
               mcw  @000@, x1          * x1 is index from 0 to 31
     chl       c    e&x1, @0@
               be   chzero
               mn   f&x1, ch&x1        * for 1, select f bit
               b    chincr
     chzero    mn   g&x1, ch&x1        * for 0, select g bit
     chincr    a    +1, x1
               mz   @0@, x1
               c    @032@, x1
               bu   chl

     * Compute temp1: k[i] + h + S1 + ch + w[i]
               cs   299
               mcw  +k-7, x3            * Convert k[i] to binary in temp1
               ma   kidx, x3
               mcw  +temp1, x1
               mcw  @008@, tobinc       * 8 hex digits
               b    tobin
               mcw  @237@, x3
               mcw  +temp1, x1
               mcw  @008@, tobinc
               b    tohex
               a    h+31, temp1+31     * +h
               a    s1+31, temp1+31    * +s1
               a    ch+31, temp1+31    * +ch
               mcw  bitidx, x1
               a    warr+31&x1, temp1+31         * + w[i]
     * Convert bit sum to 32-bit sum
               mcw  +temp1+31, x1      * x1 = right end of temp1
               b    sum
  

     * Compute s0 from a
               mcw  +a, x1
               mcw  +s0, x2
               za   +0, 31&x2               * Zero s0
     * Add a rightrotate 2
               sw   2&x2               * Wordmark at bit 2 (from left) of s0
               a    29&x1, 31&x2       * Right shifted: 31-2 = bit 29 of a, 31 = end of s0
               a    31&x1, 1&x2        * Wrapped: 31 = end of a, 2-1 = bit 1 of s0   
               cw   2&x2               * Clear wordmark
     * Add a rightrotate 13
               sw   13&x2              * Wordmark at bit 13 (from left) of s0
               a    18&x1, 31&x2       * Right shifted: 31-13 = bit 18 of a, 31 = end of s0
               a    31&x1, 12&x2       * Wrapped: 31 = end of a, 13-1 = bit 12 of s0   
               cw   13&x2              * Clear wordmark
     * Add a rightrotate 22
               sw   22&x2              * Wordmark at bit 22 (from left) of s0
               a    9&x1, 31&x2        * Right shifted: 31-22 = bit 9 of a, 31 = end of s0
               a    31&x1, 21&x2       * Wrapped: 31 = end of a, 22-1 = bit 21 of s0   
               cw   22&x2              * Clear wordmark
     * Convert sum to xor
               mcw  +s0+31, x1         * x1 = right end of s0
               mcw  @032@, x2          * Process 32 bits
               b    xor
               sw   s0                 * Restore wordmark cleared by xor

     * Compute maj(a, b, c): majority function
               za   +0, maj+31
               a    a+31, maj+31
               a    b+31, maj+31
               a    c+31, maj+31
               mz   @0@, maj+31
               mcw  @000@, x1          * x1 is index from 0 to 31
     mjl       c    maj&x1, @2@
               bh   mjzero
               mn   @1@, maj&x1       * majority of the 3 bits is 1
               b    mjincr
     mjzero    mn   @0@, maj&x1       * majority of the 3 bits is 0
     mjincr    a    +1, x1
               mz   @0@, x1
               c    @032@, x1
               bu   mjl

     * Compute temp2: S0 + maj
               za   +0, temp2+31
               a    s0+31, temp2+31
               a    maj+31, temp2+31
     * Convert bit sum to 32-bit sum
               mcw  +temp2+31, x1      * x1 = right end of temp1
               b    sum
     
               mcw  g+31, h+31         * h := g
               mcw  f+31, g+31         * g := f
               mcw  e+31, f+31         * f := e
               za   +0, e+31           * e := d + temp1
               a    d+31, e+31
               a    temp1+31, e+31
               mcw  +e+31, x1          * Convert sum to 32-bit sum
               b    sum
               mcw  c+31, d+31         * d := c
               mcw  b+31, c+31         * c := b
               mcw  a+31, b+31         * b := a
               za   +0, a+31           * a := temp1 + temp2
               a    temp1+31, a+31
               a    temp2+31, a+31
               mcw  +a+31, x1          * Convert sum to 32-bit sum
               b    sum

               a    @8@, kidx          * Increment kidx by 8 chars
               mz   @0@, kidx
               ma   @032@, bitidx      * Increment bitidx by 32 bits
               c    @!48@, bitidx      * Compare to 2048
               bu   mainlp

     * Add a-h to h0-h7
               cs   299
               mcw  @00000@, x1tmp  
     add1      mcw  x1tmp, x1
               a    a+31&x1, h0+31&x1
               ma   +h0+31, x1          * Convert sum to 32-bit sum
               b    sum     
               ma   @032@, x1tmp
               c    @00256@, x1tmp
               bu   add1
               mcw  @201@, x3
               mcw  +h0, x1
               mcw  @064@, tobinc
               b    tohex
               w
               mcw  280, 180
               p
               p

     finis     h
               b    finis

      
     * Converts sum of bits to xor
     * X1 is right end of word
     * X2 is bit count    
     * Note: clears word marks
     xor       sbr  xorx&3
     xorl      c    @000@, x2
               be   xorx
     xorfix    mz   @0@, 0&x1          * Clear zone
               c    0&x1, @2@
               bh   xorok
               sw   0&x1               * Subtract 2 and loop
               s    +2, 0&x1
               cw   0&x1
               b    xorfix
     xorok     ma   @I9I@, x1         * x1 -= 1
               s    +1, x2             * x2 -= 1
               mz   @0@, x2
               b    xorl               * loop
     
     xorx      b    @000@
     
     * Converts sum of bits to sum (i.e. propagate carries if digit > 1)
     * X1 is right end of word
     * Ends at word mark
     sum       sbr  sumx&3
     suml      mz   @0@, 0&x1          * Clear zone
               c    0&x1, @2@          * If digit is <2, then ok
               bh   sumok
               s    +2, 0&x1           * Subtract 2 from digit
               bwz  suml, 0&x1, 1      * Skip carry if at wordmark
               a    @1@, 15999&x1      * Add 1 to previous position
               b    suml               * Loop
     sumok     bwz  sumx,0&x1,1        * Quit if at wordmark
               ma   @I9I@, x1          * x1 -= 1
               b    suml               * loop
     sumx      b    @000@              * return
     
     * Converts binary to string of hex digits
     * X1 points to start (left) of binary
     * X3 points to start (left) of hex buffer
     * X1, X2, X3 destroyed
     * tobinc holds count (# of hex digits)
     tohex     sbr  tohexx&3
     tohexl    c    @000@, tobinc      * check counter
               be   tohexx
               s    @1@, tobinc        * decrement counter
               mz   @0@, tobinc
               b    tohex4
               mcw  hexchr, 0&x3
               ma   @004@, X1
               ma   @001@, X3
               b    tohexl             * loop
     tohexx    b    @000@ 
     

     
     * X1 points to 4 bits
     * Convert to hex char and write into hexchr
     * X2 destroyed

     tohex4    sbr  tohx4x&3
               mcw  @000@, x2
               c    3&X1, @1@
               bu   tohx1
               a    +1, x2
     tohx1     c    2&X1, @1@
               bu   tohx2
               a    +2, x2
     tohx2     c    1&x1, @1@
               bu   tohx4
               a    +4, x2
     tohx4     c    0&x1, @1@
               bu   tohx8
               a    +8, x2
     tohx8     mz   @0@, x2
               mcw  hextab-15&x2, hexchr
     tohx4x    b    @000@
     
     * Converts string of hex digits to binary
     * X3 points to start (left) of hex digits
     * X1 points to start (left) of binary digits
     * tobinc holds count (# of hex digits)
     * X1, X3 destroyed
     tobin     sbr  tobinx&3
     tobinl    c    @000@, tobinc      * check counter
               be   tobinx
               s    @1@, tobinc        * decrement counter
               mz   @0@, tobinc
               mcw  0&X3, hexchr
               b    tobin4             * convert 1 char
               ma   @004@, X1
               ma   @001@, X3
               b    tobinl             * loop
     tobinx    b    @000@
               
     
     tobinc    dcw  @000@
     * Convert hex digit to binary
     * Digit in hexchr (destroyed)
     * Bits written to x1, ..., x1+3
     tobin4    sbr  tobn4x&3
               mcw  @0000@, 3+x1   * Start with zero bits
               bwz  norm,hexchr,2  * Branch if no zone
              
               mcw  @1@, 0&X1
               a    @1@, hexchr    * Convert letter to value: A (1) -> 2, F (6) -> 7
               mz   @0@, hexchr
               b    tob4
     norm      c    @8@, hexchr
               bl   tob4
               mcw  @1@, 0&X1
               s    @8@, hexchr
               mz   @0@, hexchr
     tob4      c    @4@, hexchr
               bl   tob2
               mcw  @1@, 1&X1
               s    @4@, hexchr
               mz   @0@, hexchr
     tob2      c    @2@, hexchr
               bl   tob1
               mcw  @1@, 2&X1
               s    @2@, hexchr
               mz   @0@, hexchr
     tob1      c    @1@, hexchr
               bl   tobn4x
               mcw  @1@, 3&X1
     tobn4x    b    @000@          


     
     * Message schedule array is 64 entries of 32 bits = 2048 bits.
               org  3000
     warr      equ  3000
     
     s0        equ  warr+2047                *32 bits
     s1        equ  s0+32 
     ch        equ  s1+32              *32 bits

     temp1     equ  ch+32               *32 bits
     
     temp2     equ  temp1+32                *32 bits
     
     maj       equ  temp2+32                *32 bits
     
     a         equ  maj+32
     b         equ  a+32
     c         equ  b+32
     d         equ  c+32
     e         equ  d+32
     f         equ  e+32
     g         equ  f+32
     h         equ  g+32
     h0        equ  h+32
     h1        equ  h0+32
     h2        equ  h1+32
     h3        equ  h2+32
     h4        equ  h3+32
     h5        equ  h4+32
     h6        equ  h5+32
     h7        equ  h6+32
               org  h7+32
 
     hexchr    dcw  @0@
     hextab    dcw  @0123456789abcdef@    
     i         dcw  @00@               * Loop counter for w computation
     bitidx    dcw  #3
     kidx      dcw  #3         
     
     * 64 round constants for SHA-256
     k         dcw  @428a2f98@
               dcw  @71374491@
               dcw  @b5c0fbcf@
               dcw  @e9b5dba5@
               dcw  @3956c25b@
               dcw  @59f111f1@
               dcw  @923f82a4@
               dcw  @ab1c5ed5@
               dcw  @d807aa98@
               dcw  @12835b01@
               dcw  @243185be@
               dcw  @550c7dc3@
               dcw  @72be5d74@
               dcw  @80deb1fe@
               dcw  @9bdc06a7@
               dcw  @c19bf174@
               dcw  @e49b69c1@
               dcw  @efbe4786@
               dcw  @0fc19dc6@
               dcw  @240ca1cc@
               dcw  @2de92c6f@
               dcw  @4a7484aa@
               dcw  @5cb0a9dc@
               dcw  @76f988da@
               dcw  @983e5152@
               dcw  @a831c66d@
               dcw  @b00327c8@
               dcw  @bf597fc7@
               dcw  @c6e00bf3@
               dcw  @d5a79147@
               dcw  @06ca6351@
               dcw  @14292967@
               dcw  @27b70a85@
               dcw  @2e1b2138@
               dcw  @4d2c6dfc@
               dcw  @53380d13@
               dcw  @650a7354@
               dcw  @766a0abb@
               dcw  @81c2c92e@
               dcw  @92722c85@
               dcw  @a2bfe8a1@
               dcw  @a81a664b@
               dcw  @c24b8b70@
               dcw  @c76c51a3@
               dcw  @d192e819@
               dcw  @d6990624@
               dcw  @f40e3585@
               dcw  @106aa070@
               dcw  @19a4c116@
               dcw  @1e376c08@
               dcw  @2748774c@
               dcw  @34b0bcb5@
               dcw  @391c0cb3@
               dcw  @4ed8aa4a@
               dcw  @5b9cca4f@
               dcw  @682e6ff3@
               dcw  @748f82ee@
               dcw  @78a5636f@
               dcw  @84c87814@
               dcw  @8cc70208@
               dcw  @90befffa@
               dcw  @a4506ceb@
               dcw  @bef9a3f7@
               dcw  @c67178f2@
     * 8 initial hash values for SHA-256
     h0init    dcw  @6a09e667@
     h1init    dcw  @bb67ae85@
     h2init    dcw  @3c6ef372@
     h3init    dcw  @a54ff53a@
     h4init    dcw  @510e527f@
     h5init    dcw  @9b05688c@
     h6init    dcw  @1f83d9ab@
     h7init    dcw  @5be0cd19@


     input0    equ  h7init+64
               org  h7init+65

               dc   @80000000000000000000000000000000@
     input     dc   @00000000000000000000000000000100@      * 512 bits with the mostly-zero padding

               end  start

I punched the executable onto a deck of about 85 cards, which you can see at the beginning of the article. I also punched a card with the input to the hash algorithm. To run the program, I loaded the card deck into the card reader and hit the "Load" button. The cards flew through the reader at 800 cards per minute, so it took just a few seconds to load the program. The computer's console (below) flashed frantically for 40 seconds while the program ran. Finally, the printer printed out the resulting hash (as you can see at the top of the article) and the results were punched onto a new card. Since Bitcoin mining used double SHA-256 hashing, hashing for mining would take twice as long (80 seconds).

The console of the IBM 1401 shows a lot of activity while computing a SHA-256 hash.

Performance comparison

The IBM 1401 can compute a double SHA-256 hash in 80 seconds. It requires about 3000 Watts of power, roughly the same as an oven or clothes dryer. A basic IBM 1401 system sold for $125,600, which is about a million dollars in 2015 dollars. On the other hand, today you can spend $50 and get a USB stick miner with a custom ASIC integrated circuit. This USB miner performs 3.6 billion hashes per second and uses about 4 watts. The enormous difference in performance is due to several factors: the huge increase in computer speed in the last 50 years demonstrated by Moore's law, the performance lost by using a decimal business computer for a binary-based hash, and the giant speed gain from custom Bitcoin mining hardware. To summarize, to mine a block at current difficulty, the IBM 1401 would take about 5x10^14 years (about 40,000 times the current age of the universe). The electricity would cost about 10^18 dollars. And you'd get 25 bitcoins worth about $6000. Obviously, mining Bitcoin on an IBM 1401 mainframe is not a profitable venture. The photos below compare the computer circuits of the 1960s with the circuits of today, making it clear how much technology has advanced.

The Bitfury ASIC chip for mining Bitcoins does 2-3 Ghash/second. Image from http://zeptobars.ru/en/read/bitfury-bitcoin-mining-chip (CC BY 3.0 license)

On the left, SMS cards inside the IBM 1401. Each card has a handful of components and implements a circuit such as a gate. The computer contains more than a thousand of these cards. On the right, the Bitfury ASIC chip for mining Bitcoins does 2-3 Ghash/second. Image from zeptobars (CC BY 3.0 license)

Networking

You might think that Bitcoin would be impossible with 1960s technology due to the lack of networking. Would one need to mail punch cards with the blockchain to the other computers? While you might think of networked computers as a modern thing, IBM supported what they call teleprocessing as early as 1941. In the 1960s, the IBM 1401 could be hooked up to the IBM 1009 Data Transmission Unit, a modem the size of a dishwasher that could transfer up to 300 characters per second over a phone line to another computer. So it would be possible to build a Bitcoin network with 1960s-era technology. Unfortunately I didn't have teleprocessing hardware available to test this out.

IBM 1009 Data Transmission Unit. This dishwasher-sized modem was introduced in 1960 and can transmit up to 300 characters per second over phone lines. Photo from Introduction to IBM Data Processing Systems.

Conclusion

Implementing SHA-256 in assembly language for an obsolete mainframe was a challenging but interesting project. Performance was worse than I expected (even compared to my 12 minute Mandelbrot). The decimal arithmetic of a business computer is a very poor match for a binary-optimized algorithm like SHA-256. But even a computer that predates integrated circuits can implement the Bitcoin mining algorithm. And, if I ever find myself back in 1960 due to some strange time warp, now I know how to set up a Bitcoin network. The Computer History Museum in Mountain View runs demonstrations of the IBM 1401 on Wednesdays and Saturdays so if you're in the area you should definitely check it out (schedule). Tell the guys running the demo that you heard about it from me and maybe they'll run my Pi program for you. Thanks to the Computer History Museum and the members of the 1401 restoration team, Robert Garner, Ed Thelen, Van Snyder, and especially Stan Paddock. The 1401 team's website (ibm-1401.info) has a ton of interesting information about the 1401 and its restoration.

Disclaimers

I would like to be clear that I am not actually mining real Bitcoin on the IBM 1401—the Computer History Museum would probably disapprove of that. As I showed above, there's no way you could make money off mining on the IBM 1401. I did, however, really implement and run the SHA-256 algorithm on the IBM 1401, showing that mining is possible in theory. And if you're wondering how I found a successful hash, I simply used a block that had already been mined: block #286819. Email This BlogThis!Share to X Share to Facebook Share to Pinterest Labels: bitcoin, ibm1401

36 comments:

Dogzilla said... I learned Fortran in 1977 using punch cards, I feel your pain.
How many cards did you have to throw away before you had the complete program? May 23, 2015 at 9:35 AM Ken Shirriff said... Hi Dogzilla! I developed the program on the ROPE 1401 simulator, so I only needed to punch it once. The card with the Bitcoin logo, on the other hand: that took about 20 tries May 23, 2015 at 10:01 AM Dogzilla said... Lucky you!
MY first computer experience was programming a Honeywell computer using cards punched on an IBM punch card machine. I had never used a keyboard before, so errors were very common, plus, the character sets weren't 100% matches (I think the IBM punch card machine was EBCDIC). I will live forever knowing that I had to punch an '&' character for the compiler to see a '(' character. I had to type '&x+3)' if I wanted '(x+3)'.
Add to this, we were supposed to write and debug the program on paper, computer time was expensive, so we lost 5 points credit for every time we ran the deck of cards after the first.
I really enjoy your writing, especially on the Z80, since I worked on the Z80 and the 68000 while at Mostek in the early 80s.
May 23, 2015 at 11:32 AM Dogzilla said... I just finished a great book you might like. Its called "Digital Apollo - Human and Machine in Spaceflight", by D. Mindell. It covers a lot of ground about the Apollo computer and control systems, at a technical level, but you don't need to understand Control Theory to follow it. I'd call it management level. May 23, 2015 at 11:42 AM Kaos said... Very cool!
Small note: In the second to last sentence of the first paragraph:
"[...]the 1401 takes 80 seconds for a single block"
I think you meant "for a single HASH" May 23, 2015 at 11:52 AM Randy Bush said... i loved the 1401, and wished you had described it in more depth, variable length instrs, A, B, and M bits, combined op-codes (read, write, punch, and branch!), ... but i guess that is not the point of your story. good hack! May 23, 2015 at 2:00 PM Ken Shirriff said... Dogzilla: thanks for the book recommendation; I plan to look at the Apollo Guidance Computer in more detail at some point.
Kaos: I've update the text to make it clearer.
Randy: my previous article on the 1401 went into much more technical detail, so I didn't repeat the details here. May 23, 2015 at 2:45 PM Anonymous said... 12 minute mandelbrot? You and your high-end hardware. With a Casio programmable calculator from around 2010, it took almost an hour to fill the screen (written in pseudo-BASIC, ran at about 3 instructions per second).
I'll let you know if I manage to get it doing SHA-256 hashes. May 23, 2015 at 4:58 PM Geoff Ellis said... Why are you attributing the increase in computational power over the ladr few decades to moores law? Moores law was an observation and prediction. Nothing else. It was the sustained effort of many engineers over thag period. It would have happened with or without moores prediction. May 23, 2015 at 10:49 PM Ken Shirriff said... Geoff: there's a strong argument that the existence of Moore's law in fact has driven semiconductor planning and roadmaps to stay on the curve. In other words, while Moore's law was originally an observation, now it is actually driving progress.
In any case, I've changed the wording to avoid confusion. May 24, 2015 at 9:19 AM Anonymous said... Hi,
My first permanent full time job was programming a 1401. This does bring back memories :-)
Peter May 24, 2015 at 10:55 PM Anonymous said... Very interesting. But for those of us of a certain age, the 1410/7010 system was much easier to understand and much more powerful. Do any working 1410s exist anywhere? May 25, 2015 at 1:12 AM Seba said... Do you think that if you were implementing this in the sixties, you could mine an entire block, giving that difficulty at that time should be very low, or it actually depends on different factors? May 25, 2015 at 2:29 PM Anonymous said... I started on 360's but the 1403 printer lived on right until the 380's when lasers took over. And punch cards lived on too with the 2540. IIRC the 1403 shared the controller with the 2540 and that still used SMS cards. And, of course, the 360's have 1401 emulation mode which was used to encourage upgrading to 360.
May 25, 2015 at 6:38 PM ggm said... A 1960s hashing function would have been implemented in 1960s technology. SHA1/256 is not a 1960s hash function.
Cryptographic hash functions date from the 1970s. So what we'd have in the 1960s would be a simple CRC protection and then a bit more maybe.
A 1960s blockchain would have set the computability bar at the level of technology within grasp. Maybe a 1970s hash function would run faster? some kind of HMAC from the early days? May 26, 2015 at 9:57 AM Sorrel Jakins said... 1401 assembly looks like SAMOS that I had to use in Computer Science 101 in the '60's May 26, 2015 at 11:35 AM Tcat said... http://www.amazon.com/Digital-Apollo-Human-Machine-Spaceflight/dp/0262516101 May 26, 2015 at 12:46 PM Unknown said... I have very fond memories of this computer (in the guise of a 1720 that had all sorts of D/A stuff connected to the basic 1401. I remember picking up a text book on it for a class, and I had read 10+ chapters before the first class. Was a bit "greek" to me, but by the second lecture, I was hooked and WAY AHEAD of the rest of the class. This and the Physics Dept. pdp-8 became my "friends", and I have been an avid computer "hobiest" for nearly 40 years. Really glad they have two working examples of such a milestone computer! May 26, 2015 at 1:37 PM Unknown said... Ken, great blog post which is rightly getting a lot of attention. I work for IBM in the mainframe team and would love to discuss this with you further. Please Tweet me @StevenDickens3 and we can share contact details and hopefully have a chat about how we can potentially collaborate on this interesting topic. May 26, 2015 at 3:24 PM Asterix said... You should have tried this on a Model I 1620 (CADET). Does all of its arithmetic by table lookup in memory. May 28, 2015 at 11:04 AM Anonymous said... Fantastic achievement, I have had a similar idea simmering for a long time that I'd attempt to mine a bitcoin on my PDP-11/05. But that's not worth doing now, as yours trumps everything! :)
By the way are there really thousands of SMS cards in a 1401? I would have thought hundreds? May 28, 2015 at 7:15 PM Anonymous said... I remember hearing about the CADET years ago. My recollection is that CADET was actually an acronym as well as a code name:
Can't Add Doesn't Even Try
I don't know if the history is right, or just a later embellishment of the CADET name. I wrote 2 simple programs for the 1401 back in 1970-71 when I befriended one of the programmers at the High School district office. May 28, 2015 at 10:09 PM David Galloway said... So when can we expect the SMS card based hardwired Bitcoin computer? June 10, 2015 at 6:08 PM Anonymous said... I love your posts! Fantastic June 8, 2016 at 5:31 AM benwest said... this question is about pool extranonce? and prof of work related to the pool? Does the pool give every pool's miner a set of the possible values of the nonce to run through ? if we suppose a poole contain only 2 miners miner1 and miner2; and V1,V2, ..., Vn, Vn+1, ..., Vmax are the possible values of the nonce; does miner1 work with nonce values in V1, ..., Vn and miner2 work with values in Vn+1, ..., Vmax ?? ( I think the pool is like a single node of the bitcoin peer to peer network and the bitcoin-core code doesn't include a subroutine or class program about pool ????)
January 11, 2017 at 12:38 PM StefanV said... Hi Ken: Just came across your post while reading your newer one about mining with the Alto. Do you remember that Selectric printer I had back in first year at UW (the one we used to type out our entry in the shortest APL program contest)? The interface between that and my TRS-80 used a handful of SMS cards (solenoid driver cards), interfaced to some homebrew TTL logic. July 14, 2017 at 9:39 AM Unknown said... Hello Ken,
You have a really great informative blog with technology related topics, especially regarding vintage computing. Your articles are very descriptive and explain things in details, so I am able to understand them and get some insight to learn about new things. I used to collect much of the older hardware many years ago from Sparc (Sparcstations 4,5, SUN E450), PaRISC (HP 9000 712), VAX (9000 series), SGI (Indigo 2, Indy) workstations and servers, but never really managed to get good in restoring those. So I still have some of these hardware waiting for better days. In my country there are no clubs or computer museums that would connect such people with similar interests, which is a pity, because I couldn't get anyone to assist me. I also like your Bitcoin related articles, the thing about mining bitcoins on a 55-year old mainframe is just amazing, and mining them with a pencil and a paper is probably the best "magic trick" to learn after the Rubik's Cube assembly procedure to impress people, very interesting. :)
Kind regards, Jan January 6, 2018 at 2:11 AM Anonymous said... Hola! I've been reading your blog for a while now and finally got the bravery to go ahead and give you a shout out from Austin Texas! Just wanted to say keep up the great job! February 12, 2018 at 12:04 PM George Leroy Tyrebyter said... Hi Ken, it was actually the case that the 1401 had subroutines. Sure, not a stack like today for return addresses, but one did it like this:
SUBROUTINE SBR RETURN+3 Store the "B" Register
... code RETURN B 0 The 0 would be overwritten by the return address.
The 'B-Reg' held the next instruction; by storing it immediately after taking the branch that 'calls' the subroutine, as shown here, the branch at the end of the subroutine is effectively converted into a Return-From-Subroutine instruction. June 8, 2018 at 3:40 PM Stephanus said... Just when I tought I'm and old guy (born in 1970), I find you guys. June 9, 2018 at 5:55 AM gmorg said... Big big up from Italy! Your blog is awesome! June 16, 2018 at 1:52 PM John Cowan said... "Can't Add, Doesn't Even Try" is almost certainly a backronym, where the word came first and the expansion second. But yes, there were addition and multiplication tables in low memory, exactly like the ones we learned (or used to learn) in primary school, and since there was no memory protection you could easily overwrite them and corrupt the math operations to produce the wrong answers. November 8, 2018 at 9:41 AM Veli KAYA ( fearless ) said... Interesting, great job Ken. Thank you for your sharing. November 10, 2018 at 11:31 PM Unknown said... The 1401 was the first mainframe I had physical access to as a teenager learning Shelly & Cashman Structured COBOL Programming on an IBM 029 keypunch. Wonderful walk down memory lane reading this.
One issue with the article:
In the code example, this appears everywhere: "@[email protected]" (see below)
. . . * Initialize a-h from h0-h7 mcw @[email protected], x1 ilp mcw h0+31&x1, a+31&x1 ma @[email protected], x1 c x1, @[email protected] bu ilp . . .
Sadly, you and I know that it's NOT an e-mail address, it's similar to how double quotes work in BASIC, i.e.:
finished dcw @Hello World!@
Is there anything you can do to fix this in your blog?
Thanks!
- Chaz July 18, 2019 at 5:58 PM Anonymous said... Any plans to run the algorithm on the Babbage Difference Engine next? October 24, 2019 at 1:05 PM Anonymous said... Just out of curiosity and also since I'm learning to program the 1401, what is the assembly code you have presented? I don't recognise the formatting and it's probably something more advanced than what I'm currently working on, but it seems useful to know. November 28, 2022 at 3:59 PM Post a Comment Newer Post Older Post Home Contact info and site index

Search This Blog

Labels

386 6502 8008 8085 8086 8087 8088 aerospace alto analog Apollo apple arc arduino arm beaglebone bitcoin c# cadc calculator chips css datapoint dx7 electronics f# fairchild fpga fractals genome globus haskell HP html5 ibm ibm1401 ibm360 intel ipv6 ir java javascript math microcode oscilloscope Pentium photo power supply random reverse-engineering sheevaplug snark space spanish synth teardown theory unicode Z-80

Blog Archive

● ► 2026 (1) ● ► January (1) ● ► 2025 (22) ● ► December (2) ● ► November (1) ● ► October (1) ● ► September (1) ● ► August (4) ● ► July (1) ● ► June (1) ● ► May (2) ● ► April (1) ● ► March (3) ● ► February (1) ● ► January (4) ● ► 2024 (21) ● ► December (1) ● ► November (1) ● ► October (1) ● ► September (3) ● ► August (2) ● ► July (2) ● ► June (1) ● ► May (1) ● ► April (1) ● ► March (2) ● ► February (3) ● ► January (3) ● ► 2023 (35) ● ► December (4) ● ► November (2) ● ► October (3) ● ► September (1) ● ► August (2) ● ► July (3) ● ► May (1) ● ► April (2) ● ► March (4) ● ► February (5) ● ► January (8) ● ► 2022 (18) ● ► November (3) ● ► August (1) ● ► July (1) ● ► June (1) ● ► May (1) ● ► April (4) ● ► March (2) ● ► February (3) ● ► January (2) ● ► 2021 (26) ● ► December (4) ● ► November (2) ● ► September (1) ● ► August (1) ● ► July (2) ● ► June (2) ● ► May (1) ● ► April (2) ● ► March (4) ● ► February (4) ● ► January (3) ● ► 2020 (33) ● ► December (2) ● ► November (3) ● ► October (2) ● ► September (4) ● ► August (5) ● ► July (2) ● ► June (3) ● ► May (4) ● ► April (2) ● ► March (5) ● ► January (1) ● ► 2019 (18) ● ► November (3) ● ► October (2) ● ► September (3) ● ► August (1) ● ► July (4) ● ► April (2) ● ► February (1) ● ► January (2) ● ► 2018 (17) ● ► December (1) ● ► September (4) ● ► August (1) ● ► June (1) ● ► May (1) ● ► April (1) ● ► March (3) ● ► February (1) ● ► January (4) ● ► 2017 (21) ● ► December (5) ● ► November (2) ● ► October (3) ● ► August (1) ● ► July (2) ● ► June (2) ● ► April (2) ● ► March (2) ● ► February (1) ● ► January (1) ● ► 2016 (34) ● ► December (2) ● ► October (5) ● ► September (8) ● ► August (2) ● ► July (3) ● ► June (4) ● ► May (1) ● ► April (1) ● ► March (1) ● ► February (4) ● ► January (3) ● ▼ 2015 (12) ● ► December (2) ● ► November (1) ● ► October (3) ● ► August (1) ● ▼ May (2) ●Bitcoin mining on a 55 year old IBM 1401 mainframe... ●The Texas Instruments TMX 1795: the (almost) first... ● ► March (2) ● ► February (1) ● ► 2014 (13) ● ► December (1) ● ► October (1) ● ► September (3) ● ► May (2) ● ► March (1) ● ► February (5) ● ► 2013 (24) ● ► November (2) ● ► September (4) ● ► August (4) ● ► July (4) ● ► June (2) ● ► April (1) ● ► March (2) ● ► February (2) ● ► January (3) ● ► 2012 (10) ● ► December (1) ● ► November (5) ● ► October (1) ● ► May (1) ● ► March (1) ● ► February (1) ● ► 2011 (11) ● ► December (2) ● ► July (2) ● ► May (2) ● ► April (1) ● ► March (1) ● ► February (3) ● ► 2010 (22) ● ► December (2) ● ► November (4) ● ► October (3) ● ► August (1) ● ► June (1) ● ► May (2) ● ► April (3) ● ► March (4) ● ► January (2) ● ► 2009 (22) ● ► December (2) ● ► November (5) ● ► September (1) ● ► August (3) ● ► July (1) ● ► June (3) ● ► April (1) ● ► March (3) ● ► February (2) ● ► January (1) ● ► 2008 (27) ● ► July (3) ● ► June (1) ● ► May (3) ● ► April (4) ● ► March (10) ● ► February (6)

Don't miss a post!

Subscribe to get updates by email.

Built with Kit