J u m p t o c o n t e n t
M a i n m e n u
M a i n m e n u
N a v i g a t i o n
● M a i n p a g e ● C o n t e n t s ● C u r r e n t e v e n t s ● R a n d o m a r t i c l e ● A b o u t W i k i p e d i a ● C o n t a c t u s ● D o n a t e
C o n t r i b u t e
● H e l p ● L e a r n t o e d i t ● C o m m u n i t y p o r t a l ● R e c e n t c h a n g e s ● U p l o a d f i l e
S e a r c h
Search
A p p e a r a n c e
● C r e a t e a c c o u n t ● L o g i n
P e r s o n a l t o o l s
● C r e a t e a c c o u n t ● L o g i n
P a g e s f o r l o g g e d o u t e d i t o r s l e a r n m o r e ● C o n t r i b u t i o n s ● T a l k
( T o p )
1 D e f i n i t i o n
2 G e n e r a l
3 E x a m p l e s
4 F u r t h e r n o t i o n s a n d f a c t s
5 I n a b s t r a c t a l g e b r a
T o g g l e I n a b s t r a c t a l g e b r a s u b s e c t i o n
5 . 1 R i n g t h e o r y
5 . 2 D i v i s i o n l a t t i c e
6 S e e a l s o
7 N o t e s
8 C i t a t i o n s
9 R e f e r e n c e s
T o g g l e t h e t a b l e o f c o n t e n t s
D i v i s o r
6 4 l a n g u a g e s
● Æ n g l i s c ● ا ل ع ر ب ي ة ● A y m a r a r u ● ব া ং ল া ● 閩 南 語 / B â n - l â m - g ú ● Б е л а р у с к а я ● Б е л а р у с к а я ( т а р а ш к е в і ц а ) ● C a t a l à ● Ч ӑ в а ш л а ● Č e š t i n a ● D a n s k ● Ε λ λ η ν ι κ ά ● E s p a ñ o l ● E s p e r a n t o ● E u s k a r a ● ف ا ر س ی ● F r a n ç a i s ● G a l e g o ● ગ ુ જ ર ા ત ી ● 한 국 어 ● Հ ա յ ե ր ե ն ● ह ि न ् द ी ● H r v a t s k i ● I d o ● B a h a s a I n d o n e s i a ● Í s l e n s k a ● I t a l i a n o ● ע ב ר י ת ● Қ а з а қ ш а ● L a t v i e š u ● L ë t z e b u e r g e s c h ● M a g y a r ● М а к е д о н с к и ● M a l t i ● म र ा ठ ी ● မ ြ န ် မ ာ ဘ ာ သ ာ ● N a V o s a V a k a v i t i ● N e d e r l a n d s ● 日 本 語 ● N o r s k n y n o r s k ● O ʻ z b e k c h a / ў з б е к ч а ● P o l s k i ● P o r t u g u ê s ● R o m â n ă ● Р у с с к и й ● S i m p l e E n g l i s h ● S l o v e n č i n a ● S l o v e n š č i n a ● Ś l ů n s k i ● ک و ر د ی ● С р п с к и / s r p s k i ● S r p s k o h r v a t s k i / с р п с к о х р в а т с к и ● S u o m i ● S v e n s k a ● த ம ி ழ ் ● త ె ల ు గ ు ● ไ ท ย ● T ü r k ç e ● У к р а ї н с ь к а ● T i ế n g V i ệ t ● 文 言 ● 吴 语 ● 粵 語 ● 中 文
E d i t l i n k s
● A r t i c l e ● T a l k
E n g l i s h
● R e a d ● E d i t ● V i e w h i s t o r y
T o o l s
T o o l s
A c t i o n s
● R e a d ● E d i t ● V i e w h i s t o r y
G e n e r a l
● W h a t l i n k s h e r e ● R e l a t e d c h a n g e s ● U p l o a d f i l e ● S p e c i a l p a g e s ● P e r m a n e n t l i n k ● P a g e i n f o r m a t i o n ● C i t e t h i s p a g e ● G e t s h o r t e n e d U R L ● D o w n l o a d Q R c o d e ● W i k i d a t a i t e m
P r i n t / e x p o r t
● D o w n l o a d a s P D F ● P r i n t a b l e v e r s i o n
A p p e a r a n c e
F r o m W i k i p e d i a , t h e f r e e e n c y c l o p e d i a
( R e d i r e c t e d f r o m D i v i d e s )
Integer that is a factor of another integer
"Divisible" redirects here. For divisibility of groups, see
Divisible group .
The divisors of 10 illustrated with Cuisenaire rods : 1, 2, 5, and 10
In mathematics , a divisor of an integer
n ,
{\displaystyle n,}
factor of
n ,
{\displaystyle n,}
integer
m
{\displaystyle m}
n .
{\displaystyle n.}
n
{\displaystyle n}
multiple of
m .
{\displaystyle m.}
n
{\displaystyle n}
is divisible or evenly divisible by another integer
m
{\displaystyle m}
if
m
{\displaystyle m}
n
{\displaystyle n}
n
{\displaystyle n}
by
m
{\displaystyle m}
Definition [ edit ]
An integer
n
{\displaystyle n}
m
{\displaystyle m}
k
{\displaystyle k}
n =
k m .
{\displaystyle n=km.}
m ∣
n .
{\displaystyle m\mid n.}
This may be read as that
m
{\displaystyle m}
n ,
{\displaystyle n,}
m
{\displaystyle m}
n ,
{\displaystyle n,}
m
{\displaystyle m}
n ,
{\displaystyle n,}
or
n
{\displaystyle n}
m .
{\displaystyle m.}
If
m
{\displaystyle m}
n ,
{\displaystyle n,}
m ∤
n .
{\displaystyle m\not \mid n.}
There are two conventions, distinguished by whether
m
{\displaystyle m}
With the convention without an additional constraint on
m ,
{\displaystyle m,}
m ∣
0
{\displaystyle m\mid 0}
m .
{\displaystyle m.}
With the convention that
m
{\displaystyle m}
m ∣
0
{\displaystyle m\mid 0}
m .
{\displaystyle m.}
General [ edit ]
Divisors can be negative as well as positive, although often the term is restricted to positive divisors. For example, there are six divisors of 4; they are 1, 2, 4, −1, −2, and −4, but only the positive ones (1, 2, and 4) would usually be mentioned.
1 and −1 divide (are divisors of) every integer. Every integer (and its negation) is a divisor of itself. Integers divisible by 2 are called even , and integers not divisible by 2 are called odd .
1, −1,
n
{\displaystyle n}
−
n
{\displaystyle -n}
trivial divisors of
n .
{\displaystyle n.}
n
{\displaystyle n}
non-trivial divisor (or strict divisor[6] composite number , while the units −1 and 1 and prime numbers have no non-trivial divisors.
There are divisibility rules that allow one to recognize certain divisors of a number from the number's digits.
Examples [ edit ]
Plot of the number of divisors of integers from 1 to 1000. Prime numbers have exactly 2 divisors, and highly composite numbers are in bold.
7 is a divisor of 42 because
7 ×
6 =
42 ,
{\displaystyle 7\times 6=42,}
7 ∣
42.
{\displaystyle 7\mid 42.}
multiple of 7, 7 divides 42, or 7 is a factor of 42.
The non-trivial divisors of 6 are 2, −2, 3, −3.
The positive divisors of 42 are 1, 2, 3, 6, 7, 14, 21, 42.
The set of all positive divisors of 60,
A =
{
1 ,
2 ,
3 ,
4 ,
5 ,
6 ,
10 ,
12 ,
15 ,
20 ,
30 ,
60 }
,
{\displaystyle A=\{1,2,3,4,5,6,10,12,15,20,30,60\},}
partially ordered by divisibility, has the Hasse diagram :
Further notions and facts [ edit ]
There are some elementary rules:
If
a ∣
b
{\displaystyle a\mid b}
b ∣
c ,
{\displaystyle b\mid c,}
a ∣
c ,
{\displaystyle a\mid c,}
transitive relation .
If
a ∣
b
{\displaystyle a\mid b}
b ∣
a ,
{\displaystyle b\mid a,}
a =
b
{\displaystyle a=b}
or
a =
−
b .
{\displaystyle a=-b.}
If
a ∣
b
{\displaystyle a\mid b}
a ∣
c ,
{\displaystyle a\mid c,}
a ∣
(
b +
c )
{\displaystyle a\mid (b+c)}
a ∣
(
b −
c )
.
{\displaystyle a\mid (b-c).}
[a]
a ∣
b
{\displaystyle a\mid b}
c ∣
b ,
{\displaystyle c\mid b,}
(
a +
c )
∣
b
{\displaystyle (a+c)\mid b}
not always hold (e.g.
2 ∣
6
{\displaystyle 2\mid 6}
3 ∣
6
{\displaystyle 3\mid 6}
If
a ∣
b c ,
{\displaystyle a\mid bc,}
gcd
(
a ,
b )
=
1 ,
{\displaystyle \gcd(a,b)=1,}
a ∣
c .
{\displaystyle a\mid c.}
[b] Euclid's lemma .
If
p
{\displaystyle p}
p ∣
a b
{\displaystyle p\mid ab}
p ∣
a
{\displaystyle p\mid a}
or
p ∣
b .
{\displaystyle p\mid b.}
A positive divisor of
n
{\displaystyle n}
n
{\displaystyle n}
proper divisor aliquot part of
n .
{\displaystyle n.}
n
{\displaystyle n}
aliquant part of
n .
{\displaystyle n.}
An integer
n >
1
{\displaystyle n>1}
prime number . Equivalently, a prime number is a positive integer that has exactly two positive factors: 1 and itself.
Any positive divisor of
n
{\displaystyle n}
prime divisors of
n
{\displaystyle n}
fundamental theorem of arithmetic .
A number
n
{\displaystyle n}
perfect if it equals the sum of its proper divisors, deficient if the sum of its proper divisors is less than
n ,
{\displaystyle n,}
abundant if this sum exceeds
n .
{\displaystyle n.}
The total number of positive divisors of
n
{\displaystyle n}
multiplicative function
d (
n )
,
{\displaystyle d(n ),}
m
{\displaystyle m}
n
{\displaystyle n}
relatively prime , then
d (
m n )
=
d (
m )
×
d (
n )
.
{\displaystyle d(mn )=d(m )\times d(n ).}
d (
42 )
=
8 =
2 ×
2 ×
2 =
d (
2 )
×
d (
3 )
×
d (
7 )
{\displaystyle d(42 )=8=2\times 2\times 2=d(2 )\times d(3 )\times d(7 )}
m
{\displaystyle m}
n
{\displaystyle n}
d (
m n )
=
d (
m )
×
d (
n )
.
{\displaystyle d(mn )=d(m )\times d(n ).}
n
{\displaystyle n}
σ
(
n )
{\displaystyle \sigma (n )}
σ
(
42 )
=
96 =
3 ×
4 ×
8 =
σ
(
2 )
×
σ
(
3 )
×
σ
(
7 )
=
1 +
2 +
3 +
6 +
7 +
14 +
21 +
42
{\displaystyle \sigma (42 )=96=3\times 4\times 8=\sigma (2 )\times \sigma (3 )\times \sigma (7 )=1+2+3+6+7+14+21+42}
divisor functions .
prime factorization of
n
{\displaystyle n}
n =
p
1
ν
1
p
2
ν
2
⋯
p
k
ν
k
{\displaystyle n=p_{1}^{\nu _{1}}\,p_{2}^{\nu _{2}}\cdots p_{k}^{\nu _{k}}}
then the number of positive divisors of
n
{\displaystyle n}
is
d (
n )
=
(
ν
1
+
1 )
(
ν
2
+
1 )
⋯
(
ν
k
+
1 )
,
{\displaystyle d(n )=(\nu _{1}+1)(\nu _{2}+1)\cdots (\nu _{k}+1),}
and each of the divisors has the form
p
1
μ
1
p
2
μ
2
⋯
p
k
μ
k
{\displaystyle p_{1}^{\mu _{1}}\,p_{2}^{\mu _{2}}\cdots p_{k}^{\mu _{k}}}
where
0
≤
μ
i
≤
ν
i
{\displaystyle 0\leq \mu _{i}\leq \nu _{i}}
1 ≤
i ≤
k .
{\displaystyle 1\leq i\leq k.}
For every natural
n ,
{\displaystyle n,}
d (
n )
<
2
n
.
{\displaystyle d(n )<2{\sqrt {n}}.}
Also,
d (
1 )
+
d (
2 )
+
⋯
+
d (
n )
=
n ln
n +
(
2 γ
−
1 )
n +
O (
n
)
,
{\displaystyle d(1 )+d(2 )+\cdots +d(n )=n\ln n+(2\gamma -1)n+O({\sqrt {n}}),}
where
γ
{\displaystyle \gamma }
is Euler–Mascheroni constant .
One interpretation of this result is that a randomly chosen positive integer n
ln
n .
{\displaystyle \ln n.}
numbers with "abnormally many" divisors .
In abstract algebra [ edit ]
Ring theory [ edit ]
Division lattice [ edit ]
In definitions that allow the divisor to be 0, the relation of divisibility turns the set
N
{\displaystyle \mathbb {N} }
of non-negative integers into a partially ordered set that is a complete distributive lattice . The largest element of this lattice is 0 and the smallest is 1. The meet operation ∧ is given by the greatest common divisor and the join operation ∨ by the least common multiple . This lattice is isomorphic to the dual of the lattice of subgroups of the infinite cyclic group Z.
See also [ edit ]
^
a ∣
b ,
a ∣
c
{\displaystyle a\mid b,\,a\mid c}
⇒
∃
j :
j a =
b ,
∃
k :
k a =
c
{\displaystyle \Rightarrow \exists j\colon ja=b,\,\exists k\colon ka=c}
⇒
∃
j ,
k :
(
j +
k )
a =
b +
c
{\displaystyle \Rightarrow \exists j,k\colon (j+k)a=b+c}
⇒
a ∣
(
b +
c )
.
{\displaystyle \Rightarrow a\mid (b+c).}
a ∣
b ,
a ∣
c
{\displaystyle a\mid b,\,a\mid c}
⇒
∃
j :
j a =
b ,
∃
k :
k a =
c
{\displaystyle \Rightarrow \exists j\colon ja=b,\,\exists k\colon ka=c}
⇒
∃
j ,
k :
(
j −
k )
a =
b −
c
{\displaystyle \Rightarrow \exists j,k\colon (j-k)a=b-c}
⇒
a ∣
(
b −
c )
.
{\displaystyle \Rightarrow a\mid (b-c).}
^
gcd
{\displaystyle \gcd }
greatest common divisor .
Citations [ edit ]
^ "FoCaLiZe and Dedukti to the Rescue for Proof Interoperability by Raphael Cauderlier and Catherine Dubois" (PDF) .
References [ edit ]
Guy, Richard K. (2004), Unsolved Problems in Number Theory (3rd ed.), Springer Verlag , ISBN 0-387-20860-7
Hardy, G. H. ; Wright, E. M. (1960). An Introduction to the Theory of Numbers
Herstein, I. N. (1986), Abstract Algebra , New York: Macmillan Publishing Company, ISBN 0-02-353820-1
Niven, Ivan ; Zuckerman, Herbert S.; Montgomery, Hugh L. (1991). An Introduction to the Theory of Numbers (5th ed.). John Wiley & Sons . ISBN 0-471-62546-9
Øystein Ore , Number Theory and its History, McGraw–Hill, NY, 1944 (and Dover reprints).
Sims, Charles C. (1984), Abstract Algebra: A Computational Approach , New York: John Wiley & Sons, ISBN 0-471-09846-9
Tanton, James (2005). Encyclopedia of mathematics ISBN 0-8160-5124-0 OCLC 56057904 .
t
e
Divisibility-based sets of integers
Overview
Factorization forms
Constrained divisor sums
With many divisors
Aliquot sequence -related
Base -dependent
Other sets
t
e
Division and ratio
Fraction
Numerator / Denominator
R e t r i e v e d f r o m " https://en.wikipedia.org/w/index.php?title=Divisor&oldid=1215442580#Definition " C a t e g o r i e s : ● E l e m e n t a r y n u m b e r t h e o r y ● D i v i s i o n ( m a t h e m a t i c s ) H i d d e n c a t e g o r i e s : ● A r t i c l e s w i t h s h o r t d e s c r i p t i o n ● S h o r t d e s c r i p t i o n i s d i f f e r e n t f r o m W i k i d a t a ● A r t i c l e s l a c k i n g i n - t e x t c i t a t i o n s f r o m J u n e 2 0 1 5 ● A l l a r t i c l e s l a c k i n g i n - t e x t c i t a t i o n s
● T h i s p a g e w a s l a s t e d i t e d o n 2 5 M a r c h 2 0 2 4 , a t 0 4 : 3 3 ( U T C ) . ● T e x t i s a v a i l a b l e u n d e r t h e C r e a t i v e C o m m o n s A t t r i b u t i o n - S h a r e A l i k e L i c e n s e 4 . 0 ;
a d d i t i o n a l t e r m s m a y a p p l y . B y u s i n g t h i s s i t e , y o u a g r e e t o t h e T e r m s o f U s e a n d P r i v a c y P o l i c y . W i k i p e d i a ® i s a r e g i s t e r e d t r a d e m a r k o f t h e W i k i m e d i a F o u n d a t i o n , I n c . , a n o n - p r o f i t o r g a n i z a t i o n . ● P r i v a c y p o l i c y ● A b o u t W i k i p e d i a ● D i s c l a i m e r s ● C o n t a c t W i k i p e d i a ● C o d e o f C o n d u c t ● D e v e l o p e r s ● S t a t i s t i c s ● C o o k i e s t a t e m e n t ● M o b i l e v i e w

































 for every integer
for every integer  [2][3]
[2][3] be nonzero,
be nonzero,  for every nonzero integer
for every nonzero integer  [4][5]
[4][5]




 so we can say
so we can say  It can also be said that 42 is divisible by 7, 42 is a multiple of 7, 7 divides 42, or 7 is a factor of 42.
It can also be said that 42 is divisible by 7, 42 is a multiple of 7, 7 divides 42, or 7 is a factor of 42. partially ordered by divisibility, has the Hasse diagram:
partially ordered by divisibility, has the Hasse diagram: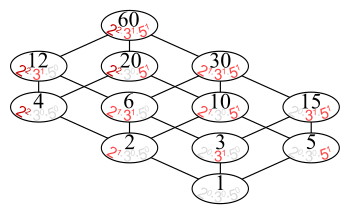
 and
and  then
then  i.e. divisibility is a transitive relation.
i.e. divisibility is a transitive relation. and
and  then
then  or
or
 and
and  then
then  holds, as does
holds, as does  [a] However, if
[a] However, if  and
and  then
then  does not always hold (e.g.
does not always hold (e.g.  and
and  but 5 does not divide 6).
but 5 does not divide 6).













































 Similarly,
Similarly, 



 refers to the greatest common divisor.
refers to the greatest common divisor.