最近、寺杣先生の「リーマン面の理論」という本を勉強しています。
第一段階として、自分自身の理解の確認のためにリーマン面の具体例を構成していきたいと思っています。今回はその前段として﹁リーマン面の定義﹂を丁寧にまとめていきたいと思います。 なお、今回の記事では﹁わかりやすく伝える﹂という意図はあまりなく、ただただ実直に定義を理解しようという考えで書いています。その点はご理解ください。
定義
のある開被覆
と、各
に対して
の開集合への同相写像
を考える。
と
の組が次を満たすとき、
はリーマン面であるという:
は正則関数
※単に「 はリーマン面である」ともいう。
①  は位相空間
は位相空間
②  は第二可算公理を満たす
は第二可算公理を満たす
の開集合全体を
として、そのある部分集合
をとります(「
のいくつかの開集合」を元とするような集合)。
の任意の開集合
が、
の部分集合
の合併によって表せるとき、つまり
③  は連結
は連結
連結の定義から「連結」のイメージが湧きづらいかもしれません。同値な定義として、 の任意の開集合
について
つまり、2枚の開集合によって
④  はハウスドルフ
はハウスドルフ
位相空間 がハウスドルフであるとは、
の任意の2点
に対して、
となるような
の開近傍
が存在するということです。
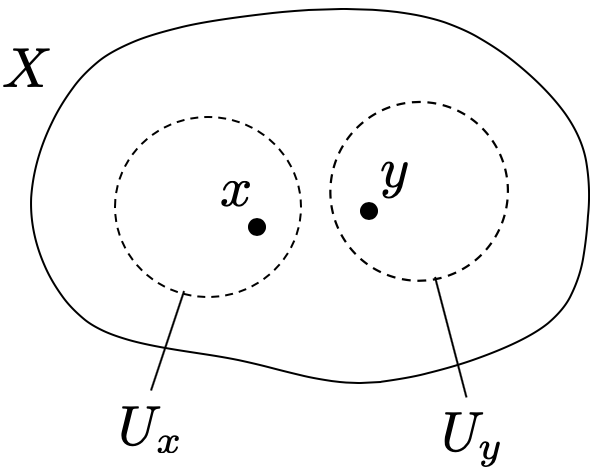
「2点が近傍によって分離できる」というのは素朴でイメージしやすい性質ですが、 がハウスドルフであることを示すのは簡単ではない場合が多そうです。
⑤  は
は  の開被覆
の開被覆
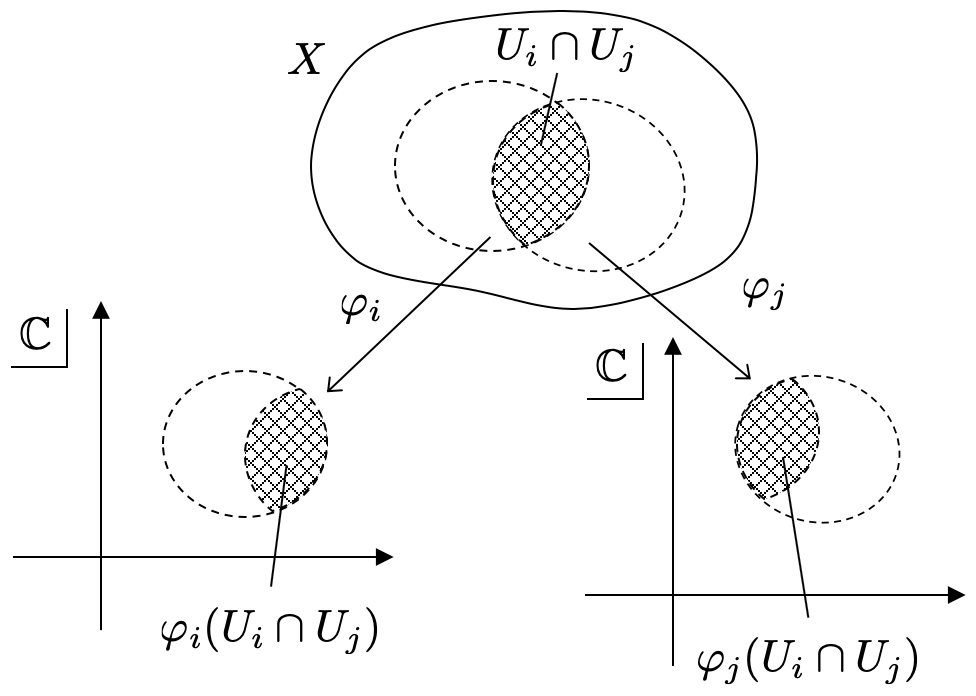
⑥  の開集合への同相写像
の開集合への同相写像 
上で定めた開被覆の各開集合 に対して、「
の開集合への同相写像
」とは、
のある開集合
に対して、同相写像

⑦  は正則関数
は正則関数
よって、次のような合成写像を考えることができます。 の逆写像
によって
を
に戻します。さらに、
によって
を
に写します。この合成写像を
とします。
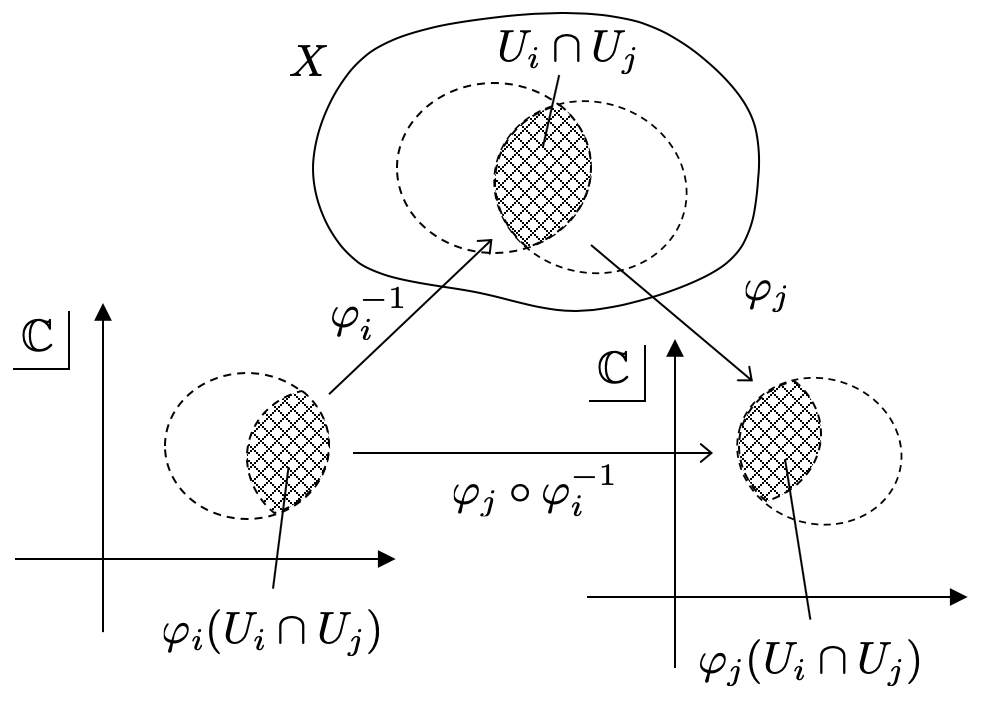
構成からわかるように、 は
の開集合から
の開集合への写像となっていますね。つまり、単なる複素関数になります。
条件⑦では、複素関数 が正則であることを要請しているというわけです。
リーマン面と多様体の関係
おわりに
2020.12.24追記
リーマン面の定義について誤解があった部分を修正しました。

2021.03.07追記
リーマン面の定義に「連結」の条件が入っていなかったので、追記しました。合わせて連結性の定義の説明を追記しました。
2021.03.08追記
「局所座標系」と書いていた部分を「座標近傍系」という呼び方に変えました。局所座標系はまた別の概念を呼ぶときに使いたいと思います。
