パラメータの推定、でもその前に
統計におけるパラメータの推定というのは大体最適化問題に帰着します。﹁なんとか関数を(最大|最小)にするようなパラーメータほにゃららを求めたい﹂とまあこんな感じで。というわけで、パラメータ推定は置いておいて、Rで最大化問題、最小化問題をどう解くかというところを最初にやってみようと思います。最適化問題は離散最適と連続のほうの最適に分けられますが、ここでは連続についての最適化問題について考えることにします。optimize関数について
Rにおける最適化をするための関数はoptim関数、optimize関数があります(他にもnlsなどありますが、とりあえずはこれが使えれば応用がききます)。
●optimize関数は1変数用の最適化をするための関数
●optim関数は2変数以上の最適化をするための関数
という感じになっています。最初は簡単なところから、ということで1変数の最適化問題を解くことにしましょう。Rにはexampleが豊富なのでexample(optimize)などとやるとoptimize関数の実際に動く例を見ることができます。最初の例を実行してみるとこんな感じになっています。
 を最小にしてください
●ただし、aは1/3です
●最適解は0.3333333で
●最適値は0です
という風に読めます。この辺の最適化は中学生でもできそうなやつですね。まあ、ただ色々エッセンスが入っていて、最大の特長としては﹁最適化したい関数を投げれる﹂というところがあります。最適化するための方法としては
●最急降下法
●ニュートン法
●共役勾配法
●準ニュートン法
●確率的勾配降下法
●etc
など様々な方法があります。﹁ちょ、統計のパラメータ求めたいだけなのに、こんなん勉強せんといかんの><課題終わらなす><﹂と涙目になりそうですが、Rならば最適化したい関数をちょっと自分で書いてあげるだけでいいんです。﹁どう最適解を求めるか﹂については切り離して考えることができるんです。ね、簡単でしょ?
を最小にしてください
●ただし、aは1/3です
●最適解は0.3333333で
●最適値は0です
という風に読めます。この辺の最適化は中学生でもできそうなやつですね。まあ、ただ色々エッセンスが入っていて、最大の特長としては﹁最適化したい関数を投げれる﹂というところがあります。最適化するための方法としては
●最急降下法
●ニュートン法
●共役勾配法
●準ニュートン法
●確率的勾配降下法
●etc
など様々な方法があります。﹁ちょ、統計のパラメータ求めたいだけなのに、こんなん勉強せんといかんの><課題終わらなす><﹂と涙目になりそうですが、Rならば最適化したい関数をちょっと自分で書いてあげるだけでいいんです。﹁どう最適解を求めるか﹂については切り離して考えることができるんです。ね、簡単でしょ?
>f<- function (x,a) (x-a)^2 > xmin <- optimize(f,c(0, 1), tol = 0.0001,a= 1/3) > xmin $minimum [1] 0.3333333 $objective [1] 0●これは関数
補足
もちろん最適化手法について知らなくてもいい、ということではありません。それぞれの最適化手法の特長を知りつつ、使い分けるなどのことが必要であったり、そもそもRで実装されていないような最適化が必要なときは自分で実装する必要があります。しかし、統計のパラメータをちょっと求めたい、というような時は最適化が本質ではありません。なので、まあRでちょこっとこういうことができたら便利だよね、ということです。
パラメータの推定
ベルヌーイ分布
すごく簡単なところからいきましょう。ベルヌーイ分布について考えていきます。これは例えばコイントスのような感じの問題です。﹁コインをn回投げました。表がk回出ました。このコインの表の出る確率はいくつでしょう?﹂というような簡単な問題です。表の出る確率を とすれば
とすれば と小学生でも大体分かりそうです。今回はこれをきちんと定式化して、Rに落とし込むというところをやってみましょう。
と小学生でも大体分かりそうです。今回はこれをきちんと定式化して、Rに落とし込むというところをやってみましょう。
定式化(尤度関数)
一回コインを投げて表が出る確率は 、裏が出る確率は
、裏が出る確率は です。﹁一回コインを投げて表が出る﹂という事象をx=1、﹁一回コインを投げて裏が出る﹂という事象をx=0とすると﹁表が出る確率は
です。﹁一回コインを投げて表が出る﹂という事象をx=1、﹁一回コインを投げて裏が出る﹂という事象をx=0とすると﹁表が出る確率は 、裏が出る確率は
、裏が出る確率は ﹂というのは次のように一つの式で書くことができてます。
﹂というのは次のように一つの式で書くことができてます。

よく分からなかったら、この式にx=1を代入すると が、この式にx=0を代入すると
が、この式にx=0を代入すると が出てくることを確認すれば大丈夫ですね。さて、これはコインを一回投げた時の式です。この式は実際に表が出たか裏が出たかによらない式になっています。そこで、コインをn回投げたときにこの式がどうなるかについて考えてみましょう。コインを毎回投げるという事象は独立*1なので、確率はこれらの積(かけ算)で書き表わすことができます。実際に書き表わしてみると
が出てくることを確認すれば大丈夫ですね。さて、これはコインを一回投げた時の式です。この式は実際に表が出たか裏が出たかによらない式になっています。そこで、コインをn回投げたときにこの式がどうなるかについて考えてみましょう。コインを毎回投げるという事象は独立*1なので、確率はこれらの積(かけ算)で書き表わすことができます。実際に書き表わしてみると

となります。この に関する関数を尤度関数と言います。﹁尤度﹂というのはどれくらい起こりやすいかを表わしているようなもので、パラメータ
に関する関数を尤度関数と言います。﹁尤度﹂というのはどれくらい起こりやすいかを表わしているようなもので、パラメータ を動かして尤度が一番大きくなるようなものを探していこうということをやります。尤度が最大になるようなパラメータのことを最尤推定量(Maximum Likelihood Estimator)と言います。今回やってみることは
●Rにおいて尤度関数を自分で表現してみる
●尤度関数を使って、最尤推定量を求めてみる
というこの二つです。さっそくやってみましょう。
を動かして尤度が一番大きくなるようなものを探していこうということをやります。尤度が最大になるようなパラメータのことを最尤推定量(Maximum Likelihood Estimator)と言います。今回やってみることは
●Rにおいて尤度関数を自分で表現してみる
●尤度関数を使って、最尤推定量を求めてみる
というこの二つです。さっそくやってみましょう。
よく分からなかったら、この式にx=1を代入すると
となります。この
尤度関数の実装
尤度は要するにn個の確率のかけ算です。一つ一つの確率は と分かっているので、n回掛けてあげれば大丈夫です。こんな感じ。
と分かっているので、n回掛けてあげれば大丈夫です。こんな感じ。
 がどういう値の時に大きいのか当たりを付けてみることにしましょう。
がどういう値の時に大きいのか当たりを付けてみることにしましょう。
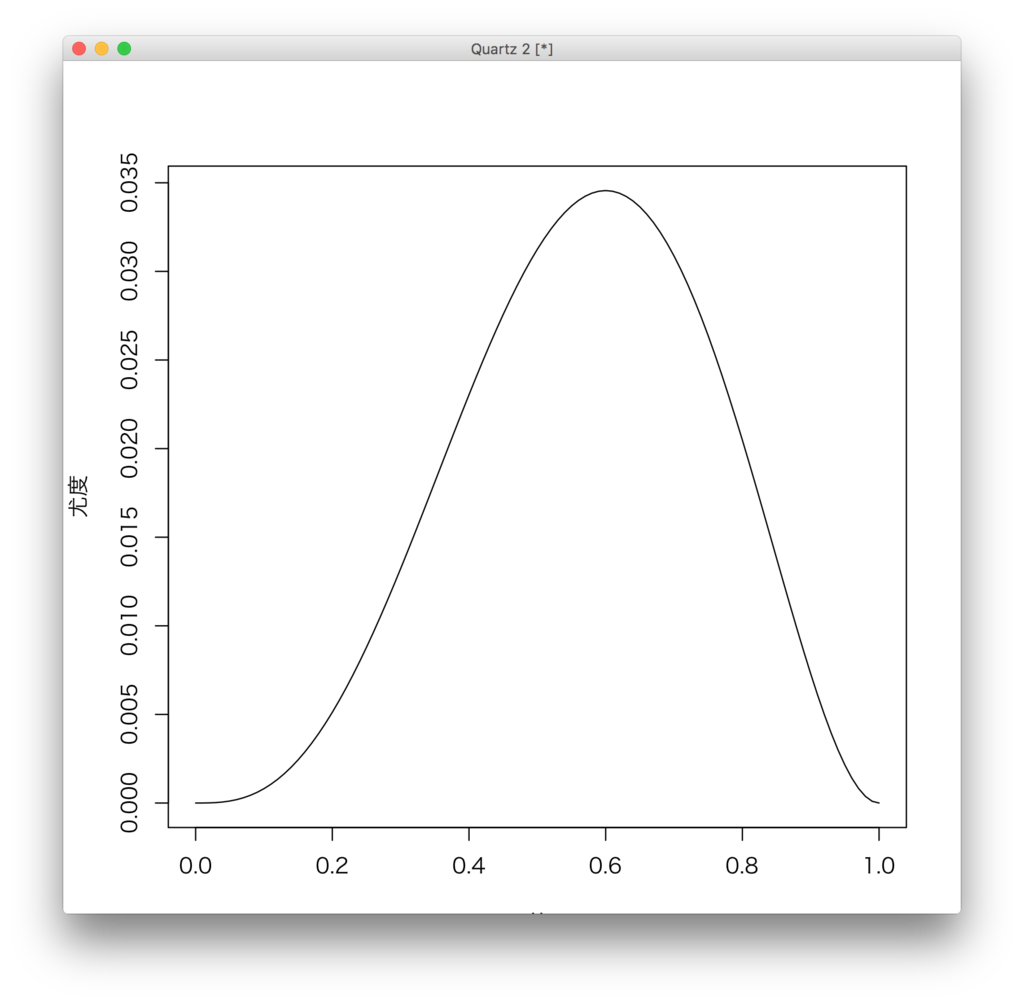 どうやら0.6のときに一番大きくなるようです。まあ、5回投げて3回表なんだから当たり前といえば当たり前ですが。
どうやら0.6のときに一番大きくなるようです。まあ、5回投げて3回表なんだから当たり前といえば当たり前ですが。
coin <-c(1, 0, 1, 1, 0) Likelihood <- function(x){ return(function(u){L<- 1 for(xninx){L<-L*u^(xn) * (1 -u)^(1-xn) } return(L) }) }ここでは、コインを5回投げて3回表が出たというのを表わしているのがcoinというオブジェクト(ベクトル)です。﹁Likelihood﹂が尤度関数です。気を付けないといけないのが、Likelihoodの戻り値が関数である、ということです。Likelihoodの戻り値は関数なので、引数に何かを入れてあげれば値を返してくれます。例えばこんな感じで。
> (Likelihood(coin))(0.5) [1] 0.03125 > (Likelihood(coin))(0.1) [1] 0.000810.5を入れたときのほうが0.1を入れたときより尤度が大きい、つまり起こりやすそうということがなんとなく分かります。せっかくRを使っているので、この尤度関数は
plot(Likelihood(coin), 0, 1, xlab="u", ylab="尤度")
 どうやら0.6のときに一番大きくなるようです。まあ、5回投げて3回表なんだから当たり前といえば当たり前ですが。
どうやら0.6のときに一番大きくなるようです。まあ、5回投げて3回表なんだから当たり前といえば当たり前ですが。
尤度関数の最適化(パラメータ推定)
さて、ここまでで尤度関数を自分で定義して、どういう形状をしているかというのが分かりました。そこで、尤度を最大にするようなパラメータ、最尤推定量をRを使って求めてみましょう。最尤推定量は尤度を最大にするパラメータですが、関数を最大にするためにはoptimize関数を使うといい、ということを先程学びました。optimizeはディフォルトで最小化をするので、最大化をするようにオプションで指定すると次のように書けます。
 対数尤度関数をplotしたものを見ると先程と形状は変わっていますが、最大となる点が大体0.6くらいで変わっていない、ということが分かります。optimize関数に対数尤度関数を投げてちゃんと
対数尤度関数をplotしたものを見ると先程と形状は変わっていますが、最大となる点が大体0.6くらいで変わっていない、ということが分かります。optimize関数に対数尤度関数を投げてちゃんと が0.6くらいになっているか確認してみましょう。optimize関数の結果の見方はもう大丈夫ですね。
が0.6くらいになっているか確認してみましょう。optimize関数の結果の見方はもう大丈夫ですね。
> optimize(f=Likelihood(coin),c(0, 1), maximum=TRUE) $maximum [1] 0.6000006 $objective [1] 0.03456●尤度を最大にしてください ●パラーメータを動かす範囲は(0,1)の間にしてください(確率なので) ●最適解(この場合は最尤推定量)は0.6000006です ●最適値は0.03456です ということを表わしています。上で見た図と結果が一致しているのでよさそうですね。 さて、最尤推定量が求められたので、それはそれでよかったのですが、統計では﹁尤度関数を最大化﹂よりも﹁対数尤度関数を最大化﹂というのをよくやります。対数尤度関数は尤度関数の対数を取ったものです。尤度関数は上にも書いたように確率の﹁かけ算﹂です。﹁対数の積は対数の和になる﹂という性質があるので、対数に確率の積を入れると確率に対数を取ったものの和で書き表わすことができます。かけ算を考えるよりも足し算を考えるほうがやりやすいので、よく﹁対数尤度関数を最大化﹂というのをやります。対数による変換は単調性があるので、最大となる点は変わりません。 さて、せっかく説明したので﹁対数尤度関数を最大化﹂をRでやってみましょう。コードはほとんど変わりません。
LogLikelihood <- function(x){ return(function(u){L<- 1 for(xninx){L<-L*u^(xn) * (1 -u)^(1-xn) } return(log(L)) }) } plot(LogLikelihood(coin), 0, 1, xlab="u", ylab="対数尤度")
 対数尤度関数をplotしたものを見ると先程と形状は変わっていますが、最大となる点が大体0.6くらいで変わっていない、ということが分かります。optimize関数に対数尤度関数を投げてちゃんと
対数尤度関数をplotしたものを見ると先程と形状は変わっていますが、最大となる点が大体0.6くらいで変わっていない、ということが分かります。optimize関数に対数尤度関数を投げてちゃんと> optimize(f=LogLikelihood(coin),c(0, 1), maximum=TRUE) $maximum [1] 0.5999985 $objective [1] -3.3650580.6くらいになっていそうです。
正規分布におけるパラメータ推定
統計学でたぶん一番使われるであろう正規分布におけるパラメータ
●平均を表わすパラメータ ●分散を表わすパラメータ
●分散を表わすパラメータ を推定する、ということをやってみましょう(尤度関数を自分で作って、それを最大にするようなパラメータを探すということ)。尤度関数を作って、それの最大化というところはベルヌーイ分布の時と大体同じですが、﹁求めないといけないパラメータが2個ある﹂という点が違うところです。optimize関数は1変数用の最適化関数でしたので、今度は2変数以上の最適化ができるoptim関数を使いましょう、ということです。
1変数の正規分布の確率密度関数は
を推定する、ということをやってみましょう(尤度関数を自分で作って、それを最大にするようなパラメータを探すということ)。尤度関数を作って、それの最大化というところはベルヌーイ分布の時と大体同じですが、﹁求めないといけないパラメータが2個ある﹂という点が違うところです。optimize関数は1変数用の最適化関数でしたので、今度は2変数以上の最適化ができるoptim関数を使いましょう、ということです。
1変数の正規分布の確率密度関数は で書き表わすことができます。ベルヌーイ分布のときと同様にn個の正規分布から発生したと仮定できるようなデータがn個あったとき、この尤度関数を求めます。尤度関数は次のように書き表わせます。
で書き表わすことができます。ベルヌーイ分布のときと同様にn個の正規分布から発生したと仮定できるようなデータがn個あったとき、この尤度関数を求めます。尤度関数は次のように書き表わせます。

さて、これを最大化してもいいのですが、さっき対数尤度関数の話をしたので、この尤度関数に対数を取ったものを考えてみましょう。すると次のようにできます。
最後のところの第一項はパラメータ と
と に関係しないので、最大化のときは忘れてかまいません。すなわち僕たちは
に関係しないので、最大化のときは忘れてかまいません。すなわち僕たちは

という関数をパラメータ と
と を動かして最大化する、ということをやるわけです。はあ長かった。。。
さて、ここまでくるとRで対数尤度関数を書くのは簡単です。こんな感じで書けます。
を動かして最大化する、ということをやるわけです。はあ長かった。。。
さて、ここまでくるとRで対数尤度関数を書くのは簡単です。こんな感じで書けます。
 、
、 と閉じた形で求めることができます。optim関数で求めた最適解がこれに一致しているか見てみましょう。
と閉じた形で求めることができます。optim関数で求めた最適解がこれに一致しているか見てみましょう。 、
、 というのは要するに平均と分散*3ですから
というのは要するに平均と分散*3ですから
さて、これを最大化してもいいのですが、さっき対数尤度関数の話をしたので、この尤度関数に対数を取ったものを考えてみましょう。すると次のようにできます。
最後のところの第一項はパラメータ
という関数をパラメータ
log_likelihood_for_norm <- function(x){ return(function(par){mu<- par[1] sigma2 <- par[2] - length(x) / 2 * log(sigma2) - 1 / 2 * sum((x-mu)^2) / sigma2 }) }まあ、何のデータに対してやってもいいんですが、Rに付属のデータのほうがやりやすいだろうということでcarsというデータフレームのspeedというカラムについてこの正規分布の最尤推定を使って、パラメータを推定します。carsのspeedというのはこんなデータです。
> cars$speed [1] 4 4 7 7 8 9 10 10 10 11 11 12 12 12 12 13 13 13 13 14 14 14 14 15 15 [26] 15 16 16 17 17 17 18 18 18 18 19 19 19 20 20 20 20 20 22 23 24 24 24 24 25さて、このcars$speedを使って、対数尤度の最大化をやってみましょう。さっそくやるとこんな感じです。
> optim(par =c(5, 10),fn= log_likelihood_for_norm(cars$speed), control = list(fnscale = -1)) $par [1] 15.39812 27.40184 $value [1] -107.7636 $counts function gradient 75 NA $convergence [1] 0 $message NULLoptimize関数と似ている感じですね。引数に与えているparはパラメータの初期値です。使う最適化によっては初期値に強く依存してしまうようなものもあるので、初期値はいくつか組み合わせて試してみるのがよいでしょう。fnは最適化したい関数。ここでは対数尤度関数ですね。control = list(fnscale = -1)というのは分かりづらいですが、optim関数もディフォルトでは最小化をすることになっているので、そうではなく最大化してくれということを伝えているだけです*2。 さて、戻り値を見てみましょう。parというのは最適解、ここでは最尤推定量で求めたかったパラメータの値です。valueは最適値です。convergenceは最適化手法を適応した結果、解が収束したかどうかを表わしています。0だと収束しています。よかったですね。 ところで、正規分布についての最尤推定量は
> mean(cars$speed) [1] 15.4 > var(cars$speed) [1] 27.95918とできます。optim関数で求めた最適解とほぼ一致しているのが分かります。 1変数の最適化と同じようにパラメータを変化させながら、対数尤度関数が最大になっていく様子を3次元にplotする、ということもRだとできます。が、似たようなことを昔書いているので、それに関してはこれを参照してください。 www.yasuhisay.info
まとめ
●Rにおける最適化をどうすればいいか見ていきました ●ベルヌーイ分布と正規分布について尤度関数、対数尤度関数がどのように定義されるかを見ていきました ●Rを使って対数尤度関数を最大にするようなパラメータ(最尤推定量)を求めました というわけでお疲れ様でした。これを元に色々な分布についてパラメータを求めてみた結果がトラックバックされてくるのを期待しています!!!
- 作者: 金谷健一
- 出版社/メーカー: 共立出版
- 発売日: 2005/09/01
- メディア: 単行本
- 購入: 29人 クリック: 424回
- この商品を含むブログ (42件) を見る