積分法

関数の定積分は、そのグラフによって囲まれる領域の符号付面積として表すことができる。

積分とは何か?（アニメーション）

積分法︵せきぶんほう、英: integral calculus︶は、微分法とともに微分積分学で対をなす主要な分野である。

説明での数式の書き方は広く普及しているライプニッツの記法に準ずる。

実数直線上の区間 [a, b] 上で定義される実変数 xの関数 fの定積分︵独: bestimmtes Integral、英: definite integral、仏: intégrale définie︶

${\displaystyle \int _{a}^{b}f($x)\,\mathrm {d} x} $\int _{a}^{b}f(x)\,\mathrm {d} x$
は、略式的に言えば fのグラフと x軸、および x= aと x= bで囲まれる xy平面の領域の符号付面積として定義される。

﹁積分﹂︵integral︶という術語は、原始関数すなわち、微分して与えられた関数 fとなるような別の関数 Fの概念を指すこともあり、その場合不定積分と呼び、

${\displaystyle F=\int f($x)\,\mathrm {d} x} $F=\int f(x)\,\mathrm {d} x$
のように書く。

積分法の原理は17世紀後半にニュートンとライプニッツが独立に定式化した。微分積分学の基本定理の発見により、それまで全く別々に発展していた積分法と微分法は深く関連付けられることになる。定理の主張は、f が閉区間 [a, b] 上の実数値連続関数ならば、f の原始関数 Fが既知であるとき、その区間上における fの定積分は

${\displaystyle \int _{a}^{b}f($x)\,\mathrm {d} x=F(b)-F(a)} $\int _{a}^{b}f(x)\,\mathrm {d} x=F(b)-F(a)$
で与えられるというものである。こうして積分と微分が微分積分学の基本的な道具となり、科学や工学において様々な応用が成された。微分積分学の創始者たちは、積分を無限小の幅を持つ矩形の無限和と考えたが、数学的に厳密な積分の定義を与えたのはリーマンである。その定義は、曲線で囲まれた領域を薄い短冊に分解して領域の面積を近似する限定的な手順に基づくものであった。19世紀に入ってから、より洗練された積分の概念が現れ始め、積分が行える領域や関数の種類が一般化されていく。線積分は二変数や三変数の関数に対して定義され、積分区間 [a, b] を平面や空間の二点を繋ぐある種の曲線で置き換えるものになっている。同様に面積分は曲線ではなく三次元空間内の曲面を考えることで得られる。また、微分形式の積分は現代的な微分幾何学において基本的な役割を演じる。これらの積分の一般化はもとは物理学の要請から生じたものであり、多くの物理法則︵特に古典電磁気学の諸法則︶の定式化に重要な役割を果たした。

これらを含め、現代的な積分の概念は様々に存在する。最も流布している積分論は、ルベーグの創始した、ルベーグ積分と呼ばれる数学的な抽象論であろう。

歴史

図形の面積や体積の求積法は、特殊なものに限れば古代からいくつも知られており、その起源は定かではないが、積分法の起源としては古代ギリシアの数学書ユークリッド原論にもある取り尽くし法︵積尽法、窄出法、英: method of exhaustion、仏: méthode d’exhaustion、独: Exhaustionsmethode、拉: methodus exhaustionibus︶などのいくつかの技法に求めることができるだろう。取り尽くし法はある領域の面積を無数の三角形で覆い尽くすことによって求めようとするものである。古代ギリシャでは、三角形を最も基本的な図形と捉えていたため、このような三角形による求積法が盛んであった。しかしたとえば、放物線︵古くは抛物線とも︶がある弦によって切り取られる面積を計算するような場合でさえ、いくらやっても三角形で覆い尽くすことはできないため、実際にはほとんどの領域で無限和の計算をすることになる。この困難に対してアルキメデスは、今で言うε-δ論法によりこの問題を回避したようである。

1635年にカヴァリエリの原理が発表され、後にエヴァンジェリスタ・トリチェリ、ピエール・ド・フェルマーが同原理の考えを用い、回転体や多項式で表される図形の求積を行った。

17世紀後半になってライプニッツとニュートンらにより微分法が発見されると、極めて技巧的な手段に頼っていた求積法は、原始関数と微分積分法の基本公式による一般的な方法で解かれることになる。18世紀にはベルヌーイらやオイラーなどによる無限小解析の発展・整備によって計算技巧は大いに発達したが、19世紀に入るとフーリエ級数の厳密な研究などを通して、初めて積分自体の意味を問わなければならない状況が生じるようになった。実際、積分の厳密な定義は、リーマンによって論文﹁任意関数の三角級数による表現の可能性について﹂︵1854年︶の中で最初に与えられた。

20世紀に入ってすぐ、やはりフーリエ級数についてなど様々な解析学上の問題に刺激されて、ルベーグは、面積や体積とは何かということに就いて深く考察することにより測度論を展開し、現在ルベーグ積分論と呼ばれているものをつくった。リーマン積分可能な関数︵ただし広義積分は含めない︶はルベーグ積分可能であるという意味では、ルベーグ積分はリーマンのそれの一般化になっている。ルベーグが測度論を用いて展開したルベーグ積分は、彼の測度論がもつ極限との親和性と抽象性から、確率論、ヒルベルト空間論、調和解析など極めて広範な応用をもち、これらは物理学や工学などで基本的な道具として用いられることとなる。

ルベーグ積分以後もさらなる一般化がされた積分法がいくつか存在する。

導入

積分は実用上の様々な状況に現れる。水泳プールが矩形状で、底面が平坦かつその長さ幅および深さが分かっているなら、プールに張ることのできる水の体積やプールの表面積やプールの縁の長さを容易に求めることができる。しかし、プールが卵形︵楕円形︶の丸い底面を持つ場合には、そういった量はどれも積分を用いる必要を生じる。実用上はこういった自明な例では近似法を用いれば十分であるかもしれないが、例えば︵任意の領域の︶精密工学ではそれらの要素の厳密値そのものが要求されることになる。

√x の 0 から 1までの積分の近似‥5個の■は右上の点を標本点として上からの評価を与え、10個の■は左上の点を標本点として下からの評価を与える。

手始めに、x = 0 から x= 1 までの間で f(x) = √x によって与えられる曲線 y= f(x) を考え、

x = 0 から x= 1 までの区間において fの下にある領域の面積はいくらか

という問いを立てて、この︵未知の︶面積を fの積分と呼んで

$\int _{0}^{1}{\sqrt {x}}\,{\rm {d}}x$$\int _{0}^{1}{\sqrt {x}}\,{\rm {d}}x$
で書き表す。最初の近似として、各辺が x= 0 から x= 1 までと y= f(0) = 0 および y= f(1) = 1 で張られるような単位正方形を考えると、その面積はちょうど 1である。実際には積分の真の値はこれよりも小さい。近似矩形の幅を減らせばよりよい結果が得られるはずであるから、近似のための分点を 1/5 、2/5 … と 1までに亘ってとり、区間を横断的に5つの短冊に分け、各短冊の右上の端点を各曲線の小片の高さ √1/5 、√2/5 … に合わせていくと、それらの矩形の面積の和をとることで、所期の積分の先ほどよりもよい近似値が

${\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\cdots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\fallingdotseq 0.7497$${\sqrt {\frac {1}{5}}}\left({\frac {1}{5}}-0\right)+{\sqrt {\frac {2}{5}}}\left({\frac {2}{5}}-{\frac {1}{5}}\right)+\cdots +{\sqrt {\frac {5}{5}}}\left({\frac {5}{5}}-{\frac {4}{5}}\right)\fallingdotseq 0.7497$
のように得られることになる。一方、各短冊の左上の端点を各曲線の小片の高さ 0 、√1/5 … に合わせた場合の、それらの矩形の面積の和は同様の計算で近似値が 0.5497 となる。

関数 fの値に隣り合う分点の差を掛けたものを無限個足し合わせることになる点に注意すれば、分点の数をどんどん多くしていくのは容易である。そうして分点がどんどん近くなるような刻み幅にしていくとしてもそれは真の値になることはない。

5つの小区間を12に増やせば面積の近似値は前者の右上の端点を用いる計算の場合 0.7036 、後者の左上の端点を用いる計算の場合 0.6203 となりその差分はより小さいものが得られる。鍵となる考え方は、分点の差に関数値を掛けて﹁無限個﹂足し合わせるということを、無限に細かい︵あるいは無限小の︶刻み幅に関数値を掛けた足し合わせに読み替えることである。

﹁実際の積分計算﹂に対しては、ニュートンとライプニッツによる微分積分学の基本定理︵微分と積分の基本的なつながりを示す定理︶が利用される。これを先ほどの平方根関数 f(x) = x^1/2 の例に適用すれば、その原始関数 f(x) = 2/3 x^3/2 に対し、単に両端の値を代入した原始関数の差 F(1) − F(0) を計算すればよい︵ 0 、1 は区間 [0, 1] の境界である︶。従って、定積分︵この曲線の下側の面積の﹁真の値﹂︶は、機械的に

${\displaystyle \int _{0}^{1}{\sqrt {x}}\,{\rm {}}dx=\int _{0}^{1}x^{\frac {1}{2}}\,{\rm {d}}x=F($1)-F(0)={\frac {2}{3}}} $\int _{0}^{1}{\sqrt {x}}\,{\rm {}}dx=\int _{0}^{1}x^{\frac {1}{2}}\,{\rm {d}}x=F(1)-F(0)={\frac {2}{3}}$
と計算することができる。

前述したとおり、短冊に分割した計算の結果は分割数を増やすほどこの値に近づく。

積分の記法

${\displaystyle \int f($x)\,{\rm {d}}x} $\int f(x)\,{\rm {d}}x$
は関数値 f(x) に微分︵微小変分︶と呼ばれる無限小の刻み幅 dxを掛けたものたちの重み付き和を Sを引き伸ばした $\int$$\int$によって表したものと見ることができる︵掛け算の記号は省略されるのが一般的である︶。

歴史的には、初期の無限小を厳密に解釈する試みが失敗したあと、リーマンが重み付き和の極限として積分を厳密に定義したものであって、それゆえに dxは差︵つまり区間の幅︶の極限を示唆したものということになる。リーマンの積分法には区間の制限や連続性の要求などからくる欠点があったことを契機として、新たな積分の定義が考え出された。特にルベーグ積分は非常に柔軟な方法で﹁測度﹂の概念を拡張する方法に基づくものである。ルベーグ積分の記法

${\displaystyle \int _{A}f($x)\,{\rm {d}}\mu } $\int _{A}f(x)\,{\rm {d}}\mu$
は、各値に割り当てられた重みが μ となるような関数値の分割から得られる重み付き和を示唆するものである。ここに Aは積分領域を表す。

微分幾何学で考察される﹁多様体上の微積分﹂には、微積分でよく使われている記法に別な解釈を与えることができる。この立場では、f (x) と dxは微分形式 ω = f(x) dx として理解され、新たに外微分と呼ばれる微分作用素 dが導入されて、微積分学の基本定理はより一般のストークスの定理‥

$\int _{A}{\rm {d}}\omega =\int _{\partial A}\omega$$\int _{A}{\rm {d}}\omega =\int _{\partial A}\omega$
として述べることができる。ストークスの定理からグリーンの定理、ガウスの発散定理および微積分学の基本定理が導出できる。

もう少し新しいところでは、超準解析のような新しい現代的な手法を通じて、無限小が厳密な意味を持って再登場している。これらの方法は黎明期の直観を正当化するのみならず、新たな数学を切り開くものとなった。

これらの積分の概念の間には差異はあるけれども、多くの部分では重なっている。例えば、楕円形の水泳プールの表面積は、プールを幾何学的に楕円として扱って、無限小の和あるいはリーマン積分やルベーグ積分として計算しても、微分形式を備えた多様体として計算しても、結果として得られる値は皆同一である。

厳密な定義

積分のきちんとした定義は様々な仕方があり、それらの全てが同値なわけではない。異なる定義が用いられるのは、その殆どが別な定義では積分が定義できない特別な場合に別な扱いを与えるためであるが、それだけでなく時に教育上の理由が介在することもある。最も広く用いられる積分法はリーマン積分とルベーグ積分である。

リーマン積分

詳細は「リーマン積分」を参照

リーマン和

実数 a、b が a< bであるとき、区間 E= [a, b] の分割とは、

$a=x_{0}<x_{1}<\cdots <x_{n}=b$$a=x_{0}<x_{1}<\cdots <x_{n}=b$
となる点の組 (x₀, …, x_n) のこと、あるいは

$E=E_{1}\cup \cdots \cup E_{n}\quad (E_{i}:=[x_{i-1},x_{i}])$$E=E_{1}\cup \cdots \cup E_{n}\quad (E_{i}:=[x_{i-1},x_{i}])$
となる小区間からなる集合 Δ = {E_i} のことである。各 x_iを区間 Eの分点、各 E_iを区間 Eの小区間または切片 (segment) という。また、分割 Δ の各切片について ξ_i ∈ E_iをあわせて考えるとき、Δ* = {(E_i, ξ_i)} を点付き分割 (tagged partition) という。

リーマン和が収斂する様子の模式図

区間 Eの点付き分割 Δ* = {(E_i, ξ_i) : E_i= [x_i−1, x_i], ξ_i ∈ E_i} があたえられたとき、

$\sum _{i=1}^{n}f(\xi _{i})\delta x_{i}\quad (\delta x_{i}:=x_{i}-x_{i-1})$$\sum _{i=1}^{n}f(\xi _{i})\delta x_{i}\quad (\delta x_{i}:=x_{i}-x_{i-1})$
の形の和を、f の点付き分割 Δ* に関するリーマン和という。

分点の個数 n+ 1 を十分大きく、切片の長さ |Δ| ≔ max{δx_i} を十分小さくするような任意の分割に関して、リーマン和の極限が有限に確定するならば、その極限を関数 fのリーマン積分と称する。またこのとき、f は︵区間 [a, b] で︶積分可能あるいは可積分︵より厳密にはリーマン積分可能あるいはリーマン可積分︶であるという。

「ダルブー積分」も参照

リーマン和、リーマン積分に関連してダルブー︵過剰・不足︶和、ダルブー︵上・下︶積分を考察することは有効である。

区間 E= [a, b] の分割 Δ = {E_i} に対して、

${\displaystyle m_{i}:=\inf\{f($x)\mid x\in E_{i}\},\quad M_{i}:=\sup\{f(x)\mid x\in E_{i}\}} $m_{i}:=\inf\{f(x)\mid x\in E_{i}\},\quad M_{i}:=\sup\{f(x)\mid x\in E_{i}\}$
とおくとき、

ある分割に対する下ダルブー和および上ダルブー和

$s_{\Delta }=\sum _{i=0}^{n-1}m_{i}\delta x_{i},\quad S_{\Delta }=\sum _{i=0}^{n-1}M_{i}\delta x_{i}$$s_{\Delta }=\sum _{i=0}^{n-1}m_{i}\delta x_{i},\quad S_{\Delta }=\sum _{i=0}^{n-1}M_{i}\delta x_{i}$
をそれぞれ、分割 Δ に関する fの下ダルブー和︵不足和︶、上ダルブー和︵過剰和︶という。このとき、m ≔ min{m_i}, M≔ max{M_i} とすれば

$m(b-a)\leq s_{\Delta }\leq \sum _{\Delta }f(\xi _{i})\delta x_{i}\leq S_{\Delta }\leq M(b-a)$$m(b-a)\leq s_{\Delta }\leq \sum _{\Delta }f(\xi _{i})\delta x_{i}\leq S_{\Delta }\leq M(b-a)$
が満たされることは明らかである。とくに、f が有界ならば︵分割 Δ のとり方に依らず︶各辺の値はいずれも有限値となる。

ダルブーの定理は下ダルブー和 s_Δ の Δ に関する上限 s, 上ダルブー和 S_Δ の下限 Sの存在をいうもので、リーマン和の極限に対して

$s\leq \lim _{|\Delta |\to 0}\sum _{\Delta }f(\xi _{i})\delta x_{i}\leq S$$s\leq \lim _{|\Delta |\to 0}\sum _{\Delta }f(\xi _{i})\delta x_{i}\leq S$
なる評価が得られる。ここに現れた sをダルブー下積分といい、S をダルブー上積分という。しばしば、s = ⨜b
a f(x)dx, S= ⨛b
a f(x)dx のようにも書かれる。すなわち記号的に、

${\displaystyle {\underline {\int _{a}\!\!\!\!}}^{\ \;b}f($x)\,dx\leq \int _{a}^{b}f(x)\,dx\leq \,{\bar {\!\int _{a}\;}}^{\!_{\scriptstyle b}}f(x)\,dx.} ${\underline {\int _{a}\!\!\!\!}}^{\ \;b}f(x)\,dx\leq \int _{a}^{b}f(x)\,dx\leq \,{\bar {\!\int _{a}\;}}^{\!_{\scriptstyle b}}f(x)\,dx.$
これから明らかなように、それらが相等しく s= Sとなることは、リーマン積分が存在することの必要十分条件であり、上積分・下積分の何れかが存在しないか存在しても一致しないときは　"リーマン積分不能" である。

ルベーグ積分

詳細は「ルベーグ積分」を参照

リーマン＝ダルブー積分（青）とルベーグ積分（赤）

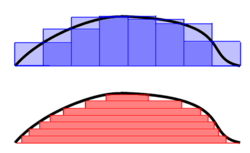
リーマン積分は広い範囲の関数や応用上重要な状況︵および理論的に興味深い状況︶では定義されないことも多い。例えば、鉄骨の密度を積分してその質量を得ることはリーマン積分で容易に求められるが、その上に静止している鉄球にまでは適応することができない。これが動機となって、より広い範囲の関数を積分することのできる新しい定義が生み出された(Rudin 1987)。特にルベーグ積分は、重み付き和の重み付けの方に注目することによってきわめて柔軟な性質を持つに至った。

ルベーグ積分の定義は測度 μ を考えることから始まる。最も単純な場合は、区間 A= [a, b] のルベーグ測度 μ(A) を区間の幅 μ(A) ≔ b− aで定義するもので、従ってルベーグ積分は、︵狭義︶リーマン積分と︵両者が存在する限りは︶一致する。より複雑な場合には、連続性も持たず、区間とは全く類似点の無いような、高度に断片化した様々な集合も測度を測ることができる。

このような柔軟性を十分に引き出すために、ルベーグ積分は重み付き和に対してリーマン積分とは﹁逆﹂なアプローチをとる。Folland (1984, p. 56)に言わせると、﹁ fのリーマン積分を計算するには領域 [a, b] を小区間に分割する﹂が、一方ルベーグ積分は﹁実質的に fの値域を分割する﹂ものである。

よくある仕方では、まず可測集合 Aの指示関数の積分の定義を

${\displaystyle \int 1_{\!A}\,{\rm {d}}\mu =\mu ($A)} $\int 1_{\!A}\,{\rm {d}}\mu =\mu (A)$
で与え、これを線型に拡張して、n 個の異なる非負の値をとる可測単関数 sに対して

${\begin{aligned}\int s\,{\rm {d}}\mu &=\int \!{\Biggl (}\sum _{i\,=\,1}^{n}a_{i}1_{\!A_{i}}{\Biggr )}{\rm {d}}\mu \\&=\sum _{i=1}^{n}a_{i}\int 1_{\!A_{i}}\,{\rm {d}}\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i})\end{aligned}}$${\begin{aligned}\int s\,{\rm {d}}\mu &=\int \!{\Biggl (}\sum _{i\,=\,1}^{n}a_{i}1_{\!A_{i}}{\Biggr )}{\rm {d}}\mu \\&=\sum _{i=1}^{n}a_{i}\int 1_{\!A_{i}}\,{\rm {d}}\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i})\end{aligned}}$
と定める︵ただし、可測集合 A_iたちは disjoint で、A_i の単関数 sによる像が定数 a_iであるものとした︶。また Eを可測集合とすれば、その上での積分を、

$\int _{E}s\,{\rm {d}}\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i}\cap E)$$\int _{E}s\,{\rm {d}}\mu =\sum _{i=1}^{n}a_{i}\,\mu (A_{i}\cap E)$
とおき、任意の非負値可測関数 fについては、下から fを近似する単関数 sの上限‥

$\int _{E}f\,d\mu =\sup \int _{E}s\,d\mu$$\int _{E}f\,d\mu =\sup \int _{E}s\,d\mu$
として fの積分を定義する。さらに一般の可測関数 fに対しては、それを正部分 f⁺ と負部分 f⁻

${\displaystyle {\begin{aligned}f^{+}($x)&{}={\begin{cases}f(x),&{\text{if }}f(x)>0\\0,&{\text{otherwise}}\end{cases}}\\[5pt]f^{-}(x)&{}={\begin{cases}-f(x),&{\text{if }}f(x)<0\\0,&{\text{otherwise}}\end{cases}}\end{aligned}}} ${\begin{aligned}f^{+}(x)&{}={\begin{cases}f(x),&{\text{if }}f(x)>0\\0,&{\text{otherwise}}\end{cases}}\\[5pt]f^{-}(x)&{}={\begin{cases}-f(x),&{\text{if }}f(x)<0\\0,&{\text{otherwise}}\end{cases}}\end{aligned}}$
に分割して、|f| := f⁺ + f⁻ に対し

$\int _{E}|f|\,d\mu <\infty$$\int _{E}|f|\,d\mu <\infty$
なるとき、f はルベーグ可積分であるといい、f の積分を

$\int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu$$\int _{E}f\,d\mu =\int _{E}f^{+}\,d\mu -\int _{E}f^{-}\,d\mu$
によって定める。

可測関数が定義される測度空間が局所コンパクトな位相空間︵よくあるのは実数全体の成す集合 R︶でもあるとき、測度はその位相と適当な意味で両立するもの︵ラドン測度‥ たとえばルベーグ測度などはそう︶を考える。そのような測度に関する積分は、コンパクト台付き連続関数の積分からはじめるような別な定義の仕方ができる。もっと具体的に述べれば、コンパクト台付き連続関数の全体はベクトル空間を成し、自然な位相を入れることができて、その空間上の任意の線型汎関数を連続にするような︵ラドン︶測度を入れることができる。従って、コンパクト台付き函関数における測度の値はその関数の積分によっても定義できる。そこからさらに測度︵＝積分︶をもっと一般の関数へ連続性によって拡張して、指示関数の積分として集合の測度を定めるのである。これは Bourbaki (2004) の取ったやり方であり、また他にも一定数の文献がこのやり方をしている。詳細はラドン測度の項へ譲る。

その他の積分

リーマン＝スティルチェス積分

リーマン＝スティルチェス積分は有界変動の関数 φ を使ったリーマン積分の拡張。
${\displaystyle \int _{a}^{b}f($x)d\varphi (x)=\lim \sum f(\xi )\delta \varphi } $\int _{a}^{b}f(x)d\varphi (x)=\lim \sum f(\xi )\delta \varphi$
φ(x) = xのときは通常のリーマン積分であり、φ が可微分で φ' が連続なら、密度を持つリーマン積分
${\displaystyle \int _{a}^{b}f($x)d\varphi (x)=\int _{a}^{b}f(x)\varphi '(x)dx} $\int _{a}^{b}f(x)d\varphi (x)=\int _{a}^{b}f(x)\varphi '(x)dx$
の形になる。

ルベーグ＝スティルチェス積分

ルベーグ＝スティルチェス積分はルベーグ積分やリーマン＝スティルチェス積分の拡張。加法的集合関数の変動が定める測度に関するルベーグ式の積分
${\displaystyle \int _{X}f($x)\,d\Phi (x)} $\int _{X}f(x)\,d\Phi (x)$
であり、ヨハン・ラドンが詳しく調べた。

ダニエル積分

ダニエル積分は積分を線型汎関数として定義する。これは測度の概念を必ずしも必要としないにもかかわらず、ルベーグ積分やルベーグ＝スティルチェス積分を含む広範な積分概念を与える。

リーマン型積分

通常のリーマン積分は、積分区間の分割の幅を一様に 0 に近づけたときの対応するリーマン和の極限として定義されるが、リーマン和の取り方や分割の幅の縮めかたを変えることによってさまざまな積分を定義でき、このように定義される積分をリーマン型積分という。たとえば、マクシェイン積分、ヘンストック・クルツヴァイル積分などのゲージ積分がリーマン型積分である。

ヤング積分

ヤング積分はリーマン＝スティルチェス積分の一般化で、有界変動関数を用いる代わりに非有界な変動の関数を用いたもの。

確率積分

伊藤積分やストラトノヴィッチ積分などのブラウン運動を伴う確率過程に対する積分

不変積分

数論や表現論の周辺分野でよく用いられる、局所コンパクト群上で定義される不変測度︵ハール測度︶に関するルベーグ式の積分。ルベーグ積分は、実数全体が加法に関して成す局所コンパクトアーベル群 R上の不変測度としてルベーグ測度をとった不変積分である︵この場合の不変は平行移動不変性を指して言う︶。

性質

被積分関数に関する線型性

有界閉区間 [a, b] 上のリーマン可積分関数全体の成す集合は、点ごとの加法 ((f + g)(x) := f(x) + g(x)) とスカラー乗法 ((αf)(x) := αf(x)) のもとでベクトル空間になり、そのような関数に対して積分をとる操作

$f\mapsto \int _{a}^{b}f\,dx$$f\mapsto \int _{a}^{b}f\,dx$
はこのベクトル空間上の線型汎関数になる。これはつまり、ひとつは可積分関数の全体が線型結合をとる操作に関して閉じていること、そしてもうひとつ

${\displaystyle \int _{a}^{b}(\alpha f+\beta g)($x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx} $\int _{a}^{b}(\alpha f+\beta g)(x)\,dx=\alpha \int _{a}^{b}f(x)\,dx+\beta \int _{a}^{b}g(x)\,dx$
のように、線型結合の積分が積分の線型結合として表されることを言っているものである。

同様に、測度 μ を持つ測度空間 E上の実数値ルベーグ可積分関数全体の成す集合は、線型結合について閉じていて線型空間を成し、ルベーグ積分をとる操作

$f\mapsto \int _{E}fd\mu$$f\mapsto \int _{E}fd\mu$
はその線型空間上の線型汎関数、すなわち

$\int _{E}(\alpha f+\beta g)\,d\mu =\alpha \int _{E}f\,d\mu +\beta \int _{E}g\,d\mu$$\int _{E}(\alpha f+\beta g)\,d\mu =\alpha \int _{E}f\,d\mu +\beta \int _{E}g\,d\mu$
を満たす。

より一般に、測度空間 (E, μ) 上で定義され局所コンパクト位相体 K上の局所コンパクト完備位相線型空間 Vに値を持つ可測関数 f: E→ V全体の成すベクトル空間を考えるとき、各関数 fに対して Vの元若しくは記号 ∞ を割り当てる写像

${\displaystyle I\colon f\mapsto I($f):=\int _{E}fd\mu } $I\colon f\mapsto I(f):=\int _{E}fd\mu$
で線型結合と両立する︵つまり I(αf + βg) = αI(f) + βI(g) を満たす︶ものとして、抽象積分を定義することができる。この状況下で、積分が有限︵すなわち割り当てられる値が Vの元︶であるような関数全体の成す部分空間を考えても、線型性は保たれる。このような形で最も重要な特別な場合が生じるのは、K が実数体 R, 複素数体 C若しくは p-進数体 Q_pの有限次拡大︵代数体︶かつ Vが有限次元ベクトル空間であるときであり、また K= Cかつ Vが複素ヒルベルト空間であるときである。

線型性に、何らかの自然な連続性と、ある種の﹁単純な﹂関数のクラスに対する正規性とを併せて考えることにより、積分の別な定義法を与えることができる。このようなやり方をするものに︵集合 X上の実数値関数の場合の︶ダニエル積分があり、またブルバキにより局所コンパクト位相線型空間に値をとる関数にまで一般化されたものがある。積分の公理的な特徴づけについては (Hildebrandt 1953) を参照されたい。

積分不等式

平均値の定理

$\inf _{a\leq x\leq b}\{f(x)\}\leq {\frac {1}{b-a}}\int _{a}^{b}f(x)\,dx\leq \sup _{a\leq x\leq b}\{f(x)\}$

被積分関数に対する積分の単調性

$f(x)\leq g(x){\mbox{ for }}\forall x\in [a,b]\Rightarrow \int _{a}^{b}f(x)dx\leq \int _{a}^{b}g(x)dx$

積分区間に対する積分の単調性

$f(x)\geq 0{\mbox{ for }}\forall x\in [a,b],\quad [c,d]\subseteq [a,b]\Rightarrow \int _{c}^{d}f(x)dx\leq \int _{a}^{b}f(x)dx$

その他の性質

積分区間に対する加法性

$\int _{a}^{\xi }f(x)\,dx+\int _{\xi }^{b}f(x)\,dx=\int _{a}^{b}f(x)\,dx$

置換積分法

（a = x(α), b = x(β) なる条件の下）

$\int _{a}^{b}f(x)dx=\int _{\alpha }^{\beta }f(x(t)){dx \over dt}dt.$

部分積分法

$\int _{a}^{b}f'(x)g(x)dx=[f(x)g(x)]_{a}^{b}-\int _{a}^{b}f(x)g'(x)dx.$

いくつかの注意

a < bならば、a を下端、b を上端とするリーマン積分は区間 [a, b] の分割からさだまるリーマン和の極限として定義されるが、a > bのときは区間 [a, b] 自体が存在しないのでそのままではリーマン和も考えることができない。しかし規約として a> bのときは

${\displaystyle \int _{a}^{b}f($x)dx:=-\int _{b}^{a}f(x)dx} $\int _{a}^{b}f(x)dx:=-\int _{b}^{a}f(x)dx$
あるいはもっと記号的に

$\int _{a}^{b}:=-\int _{b}^{a}$$\int _{a}^{b}:=-\int _{b}^{a}$
であるものとすることがしばしば行われる。この規約の元では区間に対する加法性

$\int _{a}^{b}=\int _{a}^{\gamma }+\int _{\gamma }^{b}$$\int _{a}^{b}=\int _{a}^{\gamma }+\int _{\gamma }^{b}$
は分点 γ が γ < a, a≤ γ < b, b≤ γ のいずれであるかに関わらず成立する。もっと一般に、向き付けられた d-次元多様体 Mが与えられたとき、その向きを逆にして得られる多様体を M^opとし、ω を微分 d-形式とすれば

$\int _{M}\omega =-\int _{M^{\text{op}}}\omega$$\int _{M}\omega =-\int _{M^{\text{op}}}\omega$
が成り立つ。これに対し、ルベーグ積分の文脈では Rの有限区間 E= [a, b] 上の積分

${\displaystyle \int _{E}f($x)dx=\int _{[a,b]}f(x)dx:=\int _{\mathbb {R} }\chi _{E}(x)f(x)dx} $\int _{E}f(x)dx=\int _{[a,b]}f(x)dx:=\int _{\mathbb {R} }\chi _{E}(x)f(x)dx$
とは、E の指示関数 χ_E における汎関数 dxの値であり、b < aならば Eは空集合で χ_E が恒等的に 0 となるから積分値は 0 である。

微分積分学の基本定理

詳細は「微分積分学の基本定理」を参照

微分積分学の基本定理は微分法と積分法が互いに逆の演算であることを述べるもので、連続関数を積分したものを微分すると、もとの関数に戻ることを示している。これにより、第二基本定理とも呼ばれる重要な帰結として、原始関数が既に知られている関数の定積分の計算はその原始関数を用いて計算できるようになる。

特に、これらの定理は fが [a, b] 上で連続である限り成立する。不連続関数や多変数関数への一般化は必ずしも正しくないが、一定の条件下では様々存在し、例えばストークスの定理などはそのようなものとして理解することができる。

基本定理の主張

第一基本定理

f を閉区間 [a, b] 上で定義された実数値可積分関数、F を [a, b] 上の各点 x に対して

${\displaystyle F($x)=\int _{a}^{x}f(t)\,dt} $F(x)=\int _{a}^{x}f(t)\,dt$ で定義される関数とすると、F は [a, b] 上連続である。さらに fが [a, b] 上の点 xで連続ならば Fは xにおいて可微分で、F′ = f(x) が成立する。

第二基本定理

f を閉区間 [a, b] 上で定義される実数値可積分関数で、F が [a, b] の各点 xで F′(x) = f(x) となる関数︵つまり、f の原始関数︶とすると、
${\displaystyle \int _{a}^{b}f($t)\,dt=F(b)-F(a)} $\int _{a}^{b}f(t)\,dt=F(b)-F(a)$

が成立する。

一般化

広義リーマン積分

詳細は「広義積分」を参照

無限区間における積分︵無限積分︶、無限大に発散する点を含む区間における積分︵異常積分、improper integral︶など。極限により定まる。

${\displaystyle {\begin{aligned}\int _{a}^{\infty }f($x)dx&:=\lim _{r\to \infty }\int _{a}^{r}f(x)dx,\\\int _{-\infty }^{\infty }f(x)dx&:=\lim _{s\to -\infty \atop r\to \infty }\int _{s}^{r}f(x)dx,\\\int _{0}^{1}{dx \over x^{2}}&:=\lim _{\varepsilon \to +0}\int _{\varepsilon }^{1}{dx \over x^{2}}.\end{aligned}}} ${\begin{aligned}\int _{a}^{\infty }f(x)dx&:=\lim _{r\to \infty }\int _{a}^{r}f(x)dx,\\\int _{-\infty }^{\infty }f(x)dx&:=\lim _{s\to -\infty \atop r\to \infty }\int _{s}^{r}f(x)dx,\\\int _{0}^{1}{dx \over x^{2}}&:=\lim _{\varepsilon \to +0}\int _{\varepsilon }^{1}{dx \over x^{2}}.\end{aligned}}$
これらの極限値が有限値に定まるとき、広義リーマン積分可能であるという。一方、広義リーマン積分可能でなくとも極限のとりかたを限定するとき極限値が有限確定に存在することがある。たとえば

$\int _{-1}^{1}{1 \over x}=\lim _{\varepsilon _{1}\to -0}\int _{-1}^{\varepsilon _{1}}{dx \over x}+\lim _{\varepsilon _{2}\to +0}\int _{\varepsilon _{2}}^{1}{dx \over x}$$\int _{-1}^{1}{1 \over x}=\lim _{\varepsilon _{1}\to -0}\int _{-1}^{\varepsilon _{1}}{dx \over x}+\lim _{\varepsilon _{2}\to +0}\int _{\varepsilon _{2}}^{1}{dx \over x}$
はいわゆる −∞ + ∞ の形の不定形であり、ε₁, ε₂ の 0 への近づきかたにより値が異なるため、広義リーマン積分可能でない。しかしながら ε₁ = −ε₂ という特殊な場合には

${\mbox{p.v.}}\int _{-1}^{1}{1 \over x}=\lim _{\varepsilon \to +0}\left(\int _{-1}^{-\varepsilon }{dx \over x}+\int _{\varepsilon }^{1}{dx \over x}\right)=0$${\mbox{p.v.}}\int _{-1}^{1}{1 \over x}=\lim _{\varepsilon \to +0}\left(\int _{-1}^{-\varepsilon }{dx \over x}+\int _{\varepsilon }^{1}{dx \over x}\right)=0$
となる。このように上下から同等の速さで特異点に近づける極限で現れる値をコーシーの主値という。

重積分

詳細は「重積分」を参照

曲面の下にある体積としての二重積分

区間以外の積分領域を考えることもできる。一般に写像 fの集合 E上でとった積分を

${\displaystyle \int _{E}f($x)\,dx} $\int _{E}f(x)\,dx$
で表す。このとき、x として必ずしも実数でないほかの適当な量、例えば R³のベクトルなどである場合を考えることができる。フビニの定理によれば、そのような積分が逐次積分︵累次積分︶として書けることが示される。すなわち、重積分は座標ごとに順番に積分して計算することができる。

一変数の正値関数の積分が関数のグラフと x-軸との間の領域の面積を表すのと同様に、二変数の正値関数 f(x, y) の二重積分は関数の定義する曲面 z= f(x, y) と関数の定義域を含む平面との間の領域の体積を表す︵同じ体積はこの領域を表す三次元の定数関数 F(x, y, z= f(x, y)) = 1 の三重積分としても求められる︶。同じことはさらに変数の数を増やしても成立し、積分は高次元の超体積を表すことになるが、三次元より高次元の場合は視覚化は困難である。

例えば、辺長が 4 × 6 ×5の直方体の体積は以下の二通りの方法で求めることができる。

●直方体の底面である xy-平面上の領域 D上で定数関数 f(x, y) = 5 の二重積分
$\iint _{D}5\,dx\,dy$$\iint _{D}5\,dx\,dy$ は所期の直方体の体積を与える。例えば、直方体の底面矩形が x, yの不等式 2 ≤ x≤ 6, 3 ≤ y≤ 9 で与えられているならば、上の二重積分は
$\int \limits _{3}^{9}\!\!\int \limits _{2}^{6}5\,dx\,dy$$\int \limits _{3}^{9}\!\!\int \limits _{2}^{6}5\,dx\,dy$ のことと読み替えることができる。このあと、積分を xと yのいずれから先に計算すべきなのかであるが、この例では内側の積分、つまり xに対応する区間で xに関する積分を先に行う。内側の積分を F(b) − F(a) を計算する方法などで求めた後は、得られた結果を残りの変数に関して再び積分すれば、底面と上面に挟まれた領域︵つまり所期の直方体︶の体積が求められる。

●直方体自身の上で取った定数関数1の三重積分
$\iiint \limits _{\text{cuboid}}1\,dx\,dy\,dz$$\iiint \limits _{\text{cuboid}}1\,dx\,dy\,dz$

としても所期の体積が計算できる。

線積分

詳細は「線積分」を参照

線積分は曲線に沿って元を足し合わせる

積分の概念はもっと一般の積分領域にも拡張することができる。例えば曲線や曲面を積分領域とする積分は、それぞれ線積分や面積分と呼ばれる。これらはベクトル場を扱うような物理学に応用を持つ。

線積分は曲線に沿って評価された関数の積分である。線積分にも様々なものがあり、特に閉曲線に関する線積分を周回積分などとも呼ぶ。

積分の対象となる関数はスカラー場であるかもしれないし、ベクトル場であるかもしれない。線積分の値というのは、曲線上の各点における場の値に曲線上の適当なスカラー関数︵普通は弧長、あるいはベクトル場に対しては曲線における接ベクトルとの内積︶を重みとして掛けたものの和である。この重み付けこそが、線積分と通常の区間上で定義される積分とを区別するものである。物理学における簡単な公式の多くは、線積分を用いることで自然に連続的な類似対応物に書き換えることができる。例えば、力学における仕事が力 Fと移動距離 sとの積︵ベクトル量としての点乗積︶

$W=\mathbf {F\cdot s}$$W=\mathbf {F\cdot s}$
に等しいという事実から、電場や重力場のようなベクトル場 F内の曲線に沿って動く物体に対して、その物体が場によって及ぼされる仕事の総計が、s から s+ dsまで移動する間に受ける仕事を足し合わせると考えることにより、線積分

$W=\int _{C}\mathbf {F} \cdot d\mathbf {s}$$W=\int _{C}\mathbf {F} \cdot d\mathbf {s}$
で求められる。

面積分

詳細は「面積分」を参照

面積分は曲面を微小な面素に分割して足し合わせることの極限として定義される。

面積分は空間内の曲面の上で定義される定積分で、線積分の二次元的な類似物である。積分される関数はやはりスカラー場かもしれないしベクトル場かもしれない。面積分の値というのは、曲面上の各点における場の値の総和であり、曲面を面素に分割することによって得られるリーマン和の極限として構成される。

面積分の応用例としては、曲面 S上のベクトル場 v︵つまり、S の各点 xに対して v(x) がベクトル︶が与えられているとき、S を通過する流体で xにおける流体の速度が v(x) で与えられる状況を考えればよい。流束は単位時間当たりに Sを通過する流体の量として定義される。流束を求めるためには、各点で vと単位法ベクトルとの点乗積をとる必要があり、その結果得られたスカラー場を曲面上で積分した

$\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }$$\int _{S}{\mathbf {v} }\cdot \,d{\mathbf {S} }$
が流束の値を与える︵S は Sの適当な向きの単位法ベクトル場︶。この例における流体の流束は、水や空気の流束あるいは電束や磁束といった物理的なものを想定することができる。このように面積分は物理学、特に電磁気学の古典論に応用を持つ。

微分形式の積分

詳細は「微分形式の積分」を参照

微分形式は多変数解析や微分幾何学およびテンソル論などの分野で用いられる数学的概念である。現代的な意味での微分形式は、その全体が外微分と楔積に関して︵エリ・カルタンの導入した意味での︶外積代数を成すものとして理解される。

Rⁿ の開集合 Ω 上で定義される 0-形式︵0-次微分形式︶とは単に︵ここでは︶Ω 上の滑らかな関数 fのことである。Rⁿ の m-次元の部分空間 S上での fの積分を

$\int _{S}f\,dx^{1}\cdots dx^{m}$$\int _{S}f\,dx^{1}\cdots dx^{m}$
のように書く︵上付きの数字は単に添字であって、冪指数の意味ではない︶。微分形式の文脈では、dx¹ から dxⁿまでを、リーマン和のように積分についている符牒ではなく、それ自体を形式的な対象として扱う。すなわち、これらはそれぞれ余ベクトル︵1-形式、双対ベクトル︶として捉えられ、﹁密度﹂を測るものと考えることができる︵したがって一般の意味で積分することができる︶。dx¹, …,dxⁿ は基本 1-形式と呼ばれる。

微分形式に対する楔積﹃∧﹄は双線型な﹁乗法﹂で、基本 1-形式に対する交代性

$dx^{a}\wedge dx^{a}=0$$dx^{a}\wedge dx^{a}=0$
を満足するものである。線型性と結合性を用いれば、この交代性から dx^b∧ dx^a= −dx^a ∧ dx^bが出ることに注意せよ。これはまた、楔積を取った結果が向きを持つことを保証するものでもある。

二つの基本 1-形式の楔積として得られる微分形式を基本 2-形式と呼び、同様に dx^a∧ dx^b∧ dx^cなる形で書ける微分形式を基本 3-形式と定める。以下同様に基本形式を定めるが、一般に k-形式︵k-次微分形式︶とは基本 k-形式に滑らかな関数 fによる重み付けを行った重み付き和をいう。すなわち、k-形式の全体は、基本 k-形式を基底ベクトルとするベクトル空間を成し、その係数体として 0-形式の全体がとれる。k-形式同士の楔積は、基本 k-形式の楔積を線型に拡張したものとして自然に定義できる。Rⁿ 上で、互いに線型独立な余ベクトルは高々 n-個しか取れないから、従って k> nのとき k-形式は常に 0 に等しいことが交代性から従う。

微分形式の演算には、楔積に加えて、外微分作用素 dもある。これは k-形式を (k+1)-形式へ写す作用素で、Rⁿ 上の k-形式 ω = f dx^α への dの作用は、

$d\omega =\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}dx^{i}\wedge dx^{\alpha }$$d\omega =\sum _{i=1}^{n}{\frac {\partial f}{\partial x_{i}}}dx^{i}\wedge dx^{\alpha }$
で与えられる︵α は k-次の多重指数︶。一般の k-形式へはこれを線型に拡張する。

これをもう少し一般にしたやり方で、自然に座標を用いない多様体上の積分ができるようになり、また微分積分学の基本定理の自然な一般化として︵広義の︶ストークスの定理と呼ばれる定理が得られる。ストークスの定理は、一般の k-形式 ω に対して

$\int _{\Omega }d\omega =\int _{\partial \Omega }\omega$$\int _{\Omega }d\omega =\int _{\partial \Omega }\omega$
が成り立つことを主張するものである。ただし ∂Ω は ω の積分領域 Ω の境界である。ω が 0-形式で Ω が実数直線内の閉区間である場合が微分積分学の基本定理にあたる。また、ω が 1-形式で Ω が平面上の二次元の領域であるときがグリーンの定理であり、同様に 2-形式あるいは 3-形式とホッジ双対を考えて︵狭義の︶ストークスの定理あるいは発散定理を得ることができる。このように微分形式は、積分を統一的に扱ための強力な方法を与えるものであることが分かる。

総和法

しばしば積分の離散版として総和（和分）を捉える事が行われる。たとえば無限個の数の相加平均を積分として「解釈」して定式化することができるし、ルベーグ積分の文脈では数え上げ測度に関する積分として実際に総和が現れる。

参考文献

●ベルンハルト・リーマン、足立恒雄・杉浦光夫・長岡亮介訳﹃リーマン論文集﹄朝倉書店、2004年 ISBN 978-4-254-114607

●猪狩惺﹃実解析入門﹄岩波書店

●新井仁之﹃ルベーグ積分講義﹄日本評論社

●杉浦, 光夫﹃解析入門I﹄東京大学出版会︿基礎数学2﹀、1980年。ISBN 978-4-13-062005-5。 

●伊藤, 清三﹃ルベーグ積分入門﹄︵第46版︶裳華房︿数学選書4﹀、2008年。ISBN 978-4-7853-1304-3。 

●Apostol, Tom M. (1967), Calculus, Vol. 1: One-Variable Calculus with an Introduction to Linear Algebra (2nd ed.), Wiley, ISBN 978-0-471-00005-1 

●Bourbaki, Nicolas (2004), Integration I, Springer Verlag, ISBN 3-540-41129-1 . In particular chapters III and IV.

●Burton, David M. (2005), The History of Mathematics: An Introduction (6th ed.), McGraw-Hill, p. 359, ISBN 978-0-07-305189-5 

●Cajori, Florian (1929), A History Of Mathematical Notations Volume II, Open Court Publishing, pp. 247–252, ISBN 978-0-486-67766-8, https://archive.org/details/historyofmathema027671mbp 

●Charron, Gilles; Parent, Pierre (2004), Calcul intégral manuel, Beauchemin 

●Dahlquist, Germund; Björck, Åke (2008), “Chapter 5: Numerical Integration”, Numerical Methods in Scientific Computing, Volume I, Philadelphia: SIAM, http://www.mai.liu.se/~akbjo/NMbook.html 

●Folland, Gerald B. (1984), Real Analysis: Modern Techniques and Their Applications (1st ed.), John Wiley & Sons, ISBN 978-0-471-80958-6 

●Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, p. §231, https://books.google.co.jp/books?id=TDQJAAAAIAAJ&redir_esc=y&hl=ja 
Available in translation as Fourier, Joseph (1878), The analytical theory of heat, Freeman, Alexander (trans.), Cambridge University Press, pp. 200–201, https://archive.org/details/analyticaltheory00fourrich 

●Heath, T. L., ed. (2002), The Works of Archimedes, Dover, ISBN 978-0-486-42084-4, https://archive.org/details/worksofarchimede029517mbp 
(Originally published by Cambridge University Press, 1897, based on J. L. Heiberg's Greek version.)

●Hildebrandt, T. H. (1953), “Integration in abstract spaces”, Bulletin of the American Mathematical Society 59 (2): 111–139, ISSN 0273-0979, http://projecteuclid.org/euclid.bams/1183517761 

●Kahaner, David; Moler, Cleve; Nash, Stephen (1989), “Chapter 5: Numerical Quadrature”, Numerical Methods and Software, Prentice Hall, ISBN 978-0-13-627258-8 

●Leibniz, Gottfried Wilhelm (1899), Gerhardt, Karl Immanuel, ed., Der Briefwechsel von Gottfried Wilhelm Leibniz mit Mathematikern. Erster Band, Berlin: Mayer & Müller, http://name.umdl.umich.edu/AAX2762.0001.001 

●Miller, Jeff, Earliest Uses of Symbols of Calculus, http://jeff560.tripod.com/calculus.html 2009年11月22日閲覧。 

●O’Connor, J. J.; Robertson, E. F. (1996), A history of the calculus, http://www-history.mcs.st-andrews.ac.uk/HistTopics/The_rise_of_calculus.html 2007年7月9日閲覧。 

●Rudin, Walter (1987), “Chapter 1: Abstract Integration”, Real and Complex Analysis (International ed.), McGraw-Hill, ISBN 978-0-07-100276-9 

●Saks, Stanisław (1964), Theory of the integral (English translation by L. C. Young. With two additional notes by Stefan Banach. Second revised ed.), New York: Dover, http://matwbn.icm.edu.pl/kstresc.php?tom=7&wyd=10&jez= 

●Salas, S.L. (1994), Calculus: Einführung in die Differential- und Integralrechnung, Spektrum Akademischer Verlag, ISBN 978-3-86025-1300 

●Stoer, Josef; Bulirsch, Roland (2002), “Chapter 3: Topics in Integration”, Introduction to Numerical Analysis (3rd ed.), Springer, ISBN 978-0-387-95452-3 .

●W3C (2006), Arabic mathematical notation, http://www.w3.org/TR/arabic-math/ 

●ビラン・ドゥ・アーン:﹁定積分表﹂、現代工学社︵1977年4月15日︶。

●Daniel Zwillinger:"Handbook of Integration",AK Peters,ISBN 0-86720-293-9 (1992).

●Daniel Zwillinger (Ed.): "Standard Mathematical Tables and Formulae",CRC Press,ISBN 1-43983548-9 ︵2011︶.

●I. S. Gradshteyn and M. Ryzhik, edited by Daniel Zwillinger and Victor Moll: "Table of Integrals, Series, and Products" (8th ed.),Academic Press、ISBN 978-0123849335 (2014年10月2日).

関連項目

• 微分法
• 不定積分
• 積分方程式
• ガウス求積
• 積分器
• 置換積分
• 部分積分
• 対数積分
• 微分積分学
• 解析学
• 原始関数の一覧
• 三角関数の原始関数の一覧
• 逆三角関数の原始関数の一覧
• 対数関数の原始関数の一覧
• 積の微分法則
• 商の微分法則

外部リンク

• Weisstein, Eric W. "Integral". mathworld.wolfram.com (英語).
• definite integral - PlanetMath.（英語）
• [1] by Khan Academy

オンライン本

• Keisler, H. Jerome, Elementary Calculus: An Approach Using Infinitesimals, University of Wisconsin
• Stroyan, K.D., A Brief Introduction to Infinitesimal Calculus, University of Iowa
• Mauch, Sean, Sean's Applied Math Book, CIT, an online textbook that includes a complete introduction to calculus
• Crowell, Benjamin, Calculus, Fullerton College, an online textbook
• Garrett, Paul, Notes on First-Year Calculus
• Hohenwarter, Markus; Schmidtpott, Sandra. Einführung in die Integralrechnung, Online-Lehrbuch und Aufgaben
• Hussain, Faraz, Understanding Calculus, an online textbook
• Kowalk, W.P., Integration Theory, University of Oldenburg. A new concept to an old problem. Online textbook
• Rudolph, Dennis, Integralrechnung, Online-Lehrbuch
• Sloughter, Dan, Difference Equations to Differential Equations, an introduction to calculus
• Numerical Methods of Integration at Holistic Numerical Methods Institute
• P.S. Wang, Evaluation of Definite Integrals by Symbolic Manipulation (1972) - a cookbook of definite integral techniques