Contents

Complex quadratic polynomial

Quadratic polynomials have the following properties, regardless of the form:

• It is a unicritical polynomial, i.e. it has one finite critical point in the complex plane, Dynamical plane consist of maximally 2 basins: basin of infinity and basin of finite critical point ( if finite critical point do not escapes)
• It can be postcritically finite, i.e. the orbit of the critical point can be finite, because the critical point is periodic or preperiodic.^[1]
• It is a unimodal function,
• It is a rational function,
• It is an entire function.

Forms[edit]

When the quadratic polynomial has only one variable (univariate), one can distinguish its four main forms:

• The general form: ${\displaystyle f($x)=a_{2}x^{2}+a_{1}x+a_{0}} where ${\displaystyle a_{2}\neq 0}$
• The factored form used for the logistic map: ${\displaystyle f_{r}($x)=rx(1-x)}
• ${\displaystyle f_{\theta }($x)=x^{2}+\lambda x} which has an indifferent fixed point with multiplier ${\displaystyle \lambda =e^{2\pi \theta i}}$ at the origin^[2]
• The monic and centered form, ${\displaystyle f_{c}($x)=x^{2}+c}

The monic and centered form has been studied extensively, and has the following properties:

• It is the simplest form of a nonlinear function with one coefficient (parameter),
• It is a centered polynomial (the sum of its critical points is zero).^[3]
• it is a binomial

The lambda form ${\displaystyle f_{\lambda }($z)=z^{2}+\lambda z} is:

• the simplest non-trivial perturbation of unperturbated system ${\displaystyle z\mapsto \lambda z}$
• "the first family of dynamical systems in which explicit necessary and sufficient conditions are known for when a small divisor problem is stable"^[4]

Conjugation[edit]

Between forms[edit]

Since ${\displaystyle f_{c}($x)} isaffine conjugate to the general form of the quadratic polynomial it is often used to study complex dynamics and to create images of Mandelbrot, Julia and Fatou sets.

When one wants change from ${\displaystyle \theta }$to${\displaystyle c}$:^[2]

${\displaystyle c=c(\theta )={\frac {e^{2\pi \theta i}}{2}}\left(1-{\frac {e^{2\pi \theta i}}{2}}\right).}$

When one wants change from ${\displaystyle r}$to${\displaystyle c}$, the parameter transformation is^[5]

${\displaystyle c=c($r)={\frac {1-(r-1)^{2}}{4}}=-{\frac {r}{2}}\left({\frac {r-2}{2}}\right)}

and the transformation between the variables in ${\displaystyle z_{t+1}=z_{t}^{2}+c}$ and ${\displaystyle x_{t+1}=rx_{t}(1-x_{t})}$is

${\displaystyle z=r\left({\frac {1}{2}}-x\right).}$

With doubling map[edit]

There is semi-conjugacy between the dyadic transformation (the doubling map) and the quadratic polynomial case of c = –2.

Notation[edit]

Iteration[edit]

Here ${\displaystyle f^{n}}$ denotes the n-th iterate of the function ${\displaystyle f}$:

${\displaystyle f_{c}^{n}($z)=f_{c}^{1}(f_{c}^{n-1}(z))}

so

${\displaystyle z_{n}=f_{c}^{n}(z_{0}).}$

Because of the possible confusion with exponentiation, some authors write ${\displaystyle f^{\circ n}}$ for the nth iterate of ${\displaystyle f}$.

Parameter[edit]

The monic and centered form ${\displaystyle f_{c}($x)=x^{2}+c} can be marked by:

• the parameter ${\displaystyle c}$
• the external angle ${\displaystyle \theta }$ of the ray that lands:
  • atc in Mandelbrot set on the parameter plane
  • on the critical value:z = c in Julia set on the dynamic plane

so :

${\displaystyle f_{c}=f_{\theta }}$

${\displaystyle c=c({\theta })}$

Examples:

• c is the landing point of the 1/6 external ray of the Mandelbrot set, and is ${\displaystyle z\to z^{2}+i}$ (where i^2=-1)
• c is the landing point the 5/14 external ray and is ${\displaystyle z\to z^{2}+c}$ with ${\displaystyle c=-1.23922555538957+0.412602181602004*i}$

• 
  1/4
• 
  1/6
• 
  9/56
• 
  129/16256

Map[edit]

The monic and centered form, sometimes called the Douady-Hubbard family of quadratic polynomials,^[6] is typically used with variable ${\displaystyle z}$ and parameter ${\displaystyle c}$:

${\displaystyle f_{c}($z)=z^{2}+c.}

When it is used as an evolution function of the discrete nonlinear dynamical system

${\displaystyle z_{n+1}=f_{c}(z_{n})}$

it is named the quadratic map:^[7]

${\displaystyle f_{c}:z\to z^{2}+c.}$

The Mandelbrot set is the set of values of the parameter c for which the initial condition z₀ = 0 does not cause the iterates to diverge to infinity.

Critical items[edit]

Critical points[edit]

complex plane[edit]

Acritical pointof${\displaystyle f_{c}}$ is a point ${\displaystyle z_{cr}}$onthe dynamical plane such that the derivative vanishes:

${\displaystyle f_{c}'(z_{cr})=0.}$

Since

${\displaystyle f_{c}'($z)={\frac {d}{dz}}f_{c}(z)=2z}

implies

${\displaystyle z_{cr}=0,}$

we see that the only (finite) critical point of ${\displaystyle f_{c}}$ is the point ${\displaystyle z_{cr}=0}$.

${\displaystyle z_{0}}$ is an initial point for Mandelbrot set iteration.^[8]

For the quadratic family ${\displaystyle f_{c}($z)=z^{2}+c} the critical point z = 0 is the center of symmetry of the Julia set Jc, so it is a convex combination of two points in Jc.^[9]

extended complex plane[edit]

In the Riemann sphere polynomial has 2d-2 critical points. Here zero and infinity are critical points.

Critical value[edit]

Acritical value ${\displaystyle z_{cv}}$of${\displaystyle f_{c}}$ is the image of a critical point:

${\displaystyle z_{cv}=f_{c}(z_{cr})}$

Since

${\displaystyle z_{cr}=0}$

we have

${\displaystyle z_{cv}=c}$

So the parameter ${\displaystyle c}$ is the critical value of ${\displaystyle f_{c}($z)} .

Critical level curves[edit]

A critical level curve the level curve which contain critical point. It acts as a sort of skeleton^[10] of dynamical plane

Example : level curves cross at saddle point, which is a special type of critical point.

• 
  attracting
• 
  attracting
• 
  attracting
• 
  parabolic
• Video for c along internal ray 0

Critical limit set[edit]

Critical limit set is the set of forward orbit of all critical points

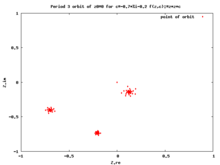
Critical orbit[edit]

The forward orbit of a critical point is called a critical orbit. Critical orbits are very important because every attracting periodic orbit attracts a critical point, so studying the critical orbits helps us understand the dynamics in the Fatou set.^[11][12][13]

${\displaystyle z_{0}=z_{cr}=0}$

${\displaystyle z_{1}=f_{c}(z_{0})=c}$

${\displaystyle z_{2}=f_{c}(z_{1})=c^{2}+c}$

${\displaystyle z_{3}=f_{c}(z_{2})=(c^{2}+c)^{2}+c}$

${\displaystyle \ \vdots }$

This orbit falls into an attracting periodic cycle if one exists.

Critical sector[edit]

The critical sector is a sector of the dynamical plane containing the critical point.

Critical set[edit]

Critical set is a set of critical points

Critical polynomial[edit]

${\displaystyle P_{n}($c)=f_{c}^{n}(z_{cr})=f_{c}^{n}(0)}

so

${\displaystyle P_{0}($c)=0}

${\displaystyle P_{1}($c)=c}

${\displaystyle P_{2}($c)=c^{2}+c}

${\displaystyle P_{3}($c)=(c^{2}+c)^{2}+c}

These polynomials are used for:

• finding centers of these Mandelbrot set components of period n. Centers are rootsofn-th critical polynomials

${\displaystyle {\text{centers}}=\{c:P_{n}($c)=0\}}

• finding roots of Mandelbrot set components of period n (local minimumof${\displaystyle P_{n}($c)} )
• Misiurewicz points

${\displaystyle M_{n,k}=\{c:P_{k}($c)=P_{k+n}(c)\}}

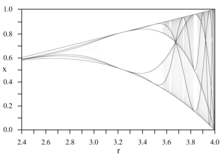
Critical curves[edit]

Diagrams of critical polynomials are called critical curves.^[14]

These curves create the skeleton (the dark lines) of a bifurcation diagram.^[15][16]

Spaces, planes[edit]

4D space[edit]

One can use the Julia-Mandelbrot 4-dimensional (4D) space for a global analysis of this dynamical system.^[17]

In this space there are two basic types of 2D planes:

• the dynamical (dynamic) plane, ${\displaystyle f_{c}}$-plane or c-plane
• the parameter plane or z-plane

There is also another plane used to analyze such dynamical systems w-plane:

• the conjugation plane^[18]
• model plane^[19]

2D Parameter plane[edit]

• Parameter plane types
• 
  r parameter plane (logistic map)
• 
  c parameter plane

The phase space of a quadratic map is called its parameter plane. Here:

${\displaystyle z_{0}=z_{cr}}$ is constant and ${\displaystyle c}$ is variable.

There is no dynamics here. It is only a set of parameter values. There are no orbits on the parameter plane.

The parameter plane consists of:

• The Mandelbrot set
  • The bifurcation locus = boundary of Mandelbrot set with
    • root points
  • Bounded hyperbolic components of the Mandelbrot set = interior of Mandelbrot set^[20] with internal rays
• exterior of Mandelbrot set with
  • external rays
  • equipotential lines

There are many different subtypes of the parameter plane.^[21][22]

See also :

• Boettcher map which maps exterior of Mandelbrot set to the exterior of unit disc
• multiplier map which maps interior of hyperbolic component of Mandelbrot set to the interior of unit disc

2D Dynamical plane[edit]

"The polynomial Pc maps each dynamical ray to another ray doubling the angle (which we measure in full turns, i.e. 0 = 1 = 2π rad = 360°), and the dynamical rays of any polynomial "look like straight rays" near infinity. This allows us to study the Mandelbrot and Julia sets combinatorially, replacing the dynamical plane by the unit circle, rays by angles, and the quadratic polynomial by the doubling modulo one map." Virpi Kauko^[23]

On the dynamical plane one can find:

• The Julia set
• The Filled Julia set
• The Fatou set
• Orbits

The dynamical plane consists of:

• Fatou set
• Julia set

Here, ${\displaystyle c}$ is a constant and ${\displaystyle z}$ is a variable.

The two-dimensional dynamical plane can be treated as a Poincaré cross-section of three-dimensional space of continuous dynamical system.^[24][25]

Dynamical z-planes can be divided into two groups:

• ${\displaystyle f_{0}}$ plane for ${\displaystyle c=0}$ (see complex squaring map)
• ${\displaystyle f_{c}}$ planes (all other planes for ${\displaystyle c\neq 0}$)

Riemann sphere[edit]

The extended complex plane plus a point at infinity

• the Riemann sphere

Derivatives[edit]

First derivative with respect to c[edit]

On the parameter plane:

• ${\displaystyle c}$ is a variable
• ${\displaystyle z_{0}=0}$ is constant

The first derivativeof${\displaystyle f_{c}^{n}(z_{0})}$ with respect to cis

${\displaystyle z_{n}'={\frac {d}{dc}}f_{c}^{n}(z_{0}).}$

This derivative can be found by iteration starting with

${\displaystyle z_{0}'={\frac {d}{dc}}f_{c}^{0}(z_{0})=1}$

and then replacing at every consecutive step

${\displaystyle z_{n+1}'={\frac {d}{dc}}f_{c}^{n+1}(z_{0})=2\cdot {}f_{c}^{n}($z)\cdot {\frac {d}{dc}}f_{c}^{n}(z_{0})+1=2\cdot z_{n}\cdot z_{n}'+1.}

This can easily be verified by using the chain rule for the derivative.

This derivative is used in the distance estimation method for drawing a Mandelbrot set.

First derivative with respect to z[edit]

On the dynamical plane:

• ${\displaystyle z}$ is a variable;
• ${\displaystyle c}$ is a constant.

At a fixed point ${\displaystyle z_{0}}$,

${\displaystyle f_{c}'(z_{0})={\frac {d}{dz}}f_{c}(z_{0})=2z_{0}.}$

At a periodic point z₀ of period p the first derivative of a function

${\displaystyle (f_{c}^{p})'(z_{0})={\frac {d}{dz}}f_{c}^{p}(z_{0})=\prod _{i=0}^{p-1}f_{c}'(z_{i})=2^{p}\prod _{i=0}^{p-1}z_{i}=\lambda }$

is often represented by ${\displaystyle \lambda }$ and referred to as the multiplier or the Lyapunov characteristic number. Its logarithm is known as the Lyapunov exponent. Absolute value of multiplier is used to check the stabilityofperiodic (also fixed) points.

At a nonperiodic point, the derivative, denoted by ${\displaystyle z'_{n}}$, can be found by iteration starting with

${\displaystyle z'_{0}=1,}$

and then using

${\displaystyle z'_{n}=2*z_{n-1}*z'_{n-1}.}$

This derivative is used for computing the external distance to the Julia set.

Schwarzian derivative[edit]

The Schwarzian derivative (SD for short) of f is:^[26]

${\displaystyle ($Sf)(z)={\frac {f'''(z)}{f'(z)}}-{\frac {3}{2}}\left({\frac {f''(z)}{f'(z)}}\right)^{2}.}

See also[edit]

• Misiurewicz point
• Periodic points of complex quadratic mappings
• Mandelbrot set
• Julia set
• Milnor–Thurston kneading theory
• Tent map
• Logistic map

References[edit]

External links[edit]

Wikimedia Commons has media related to Complex quadratic polynomials.

• Monica Nevins and Thomas D. Rogers, "Quadratic maps as dynamical systems on the p-adic numbers^{[permanent dead link]}"
• Wolf Jung : Homeomorphisms on Edges of the Mandelbrot Set. Ph.D. thesis of 2002
• More about Quadratic Maps : Quadratic Map