Jump to content

Main menu Navigation ●Main page ●Contents ●Current events ●Random article ●About Wikipedia ●Contact us ●Donate Contribute ●Help ●Learn to edit ●Community portal ●Recent changes ●Upload file

●Create account ●Log in ●Create account ● Log in Pages for logged out editors learn more ●Contributions ●Talk

(Top) 1Definition 2Special cases 3Properties 3.1Generalized mean inequality 4Proof of the weighted inequality 4.1Equivalence of inequalities between means of opposite signs 4.2Geometric mean 4.3Inequality between any two power means 5Generalized f-mean 6Applications 6.1Signal processing 7See also 8Notes 9References 10Further reading 11External links

Generalized mean

●Български ●Dansk ●Deutsch ●Español ●Euskara ●فارسی ●Français ●Galego ●한국어 ●हिन्दी ●עברית ●Magyar ●Nederlands ●日本語 ●Polski ●Русский ●Српски / srpski ●Svenska ●தமிழ் ●Türkçe ●Українська ●中文 Edit links ●Article ●Talk ●Read ●Edit ●View history Tools Actions ●Read ●Edit ●View history General ●What links here ●Related changes ●Upload file ●Special pages ●Permanent link ●Page information ●Cite this page ●Get shortened URL ●Download QR code ●Wikidata item Print/export ●Download as PDF ●Printable version From Wikipedia, the free encyclopedia

This article needs additional citations for verification. Please help improve this articlebyadding citations to reliable sources. Unsourced material may be challenged and removed.
Find sources: "Generalized mean" – news · newspapers · books · scholar · JSTOR (June 2020) (Learn how and when to remove this message)

Plot of several generalized means

M_{p}(1,x)

Inmathematics, generalized means (orpower meanorHölder mean from Otto Hölder)^[1] are a family of functions for aggregating sets of numbers. These include as special cases the Pythagorean means (arithmetic, geometric, and harmonic means).

Definition[edit]

If $p$ is a non-zero real number, and $x_{1},\dots ,x_{n}$ are positive real numbers, then the generalized meanorpower mean with exponent $p$ of these positive real numbers is^[2]^[3]

M_{p}(x_{1},\dots ,x_{n})=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{p}\right)^{{1}/{p}}.

M_{p}(x_{1},\dots ,x_{n})=\left({\frac {1}{n}}\sum _{i=1}^{n}x_{i}^{p}\right)^{{1}/{p}}.

(See $p$ -norm). For $p = 0$ we set it equal to the geometric mean (which is the limit of means with exponents approaching zero, as proved below):

M_{0}(x_{1},\dots ,x_{n})=\left(\prod _{i=1}^{n}x_{i}\right)^{1/n}.

M_{0}(x_{1},\dots ,x_{n})=\left(\prod _{i=1}^{n}x_{i}\right)^{1/n}.

Furthermore, for a sequence of positive weights $w i$ we define the weighted power meanas^[2]

M_{p}(x_{1},\dots ,x_{n})=\left({\frac {\sum _{i=1}^{n}w_{i}x_{i}^{p}}{\sum _{i=1}^{n}w_{i}}}\right)^{{1}/{p}}

M_{p}(x_{1},\dots ,x_{n})=\left({\frac {\sum _{i=1}^{n}w_{i}x_{i}^{p}}{\sum _{i=1}^{n}w_{i}}}\right)^{{1}/{p}}

and when

p = 0

, it is equal to the weighted geometric mean:

M_{0}(x_{1},\dots ,x_{n})=\left(\prod _{i=1}^{n}x_{i}^{w_{i}}\right)^{1/\sum _{i=1}^{n}w_{i}}.

M_{0}(x_{1},\dots ,x_{n})=\left(\prod _{i=1}^{n}x_{i}^{w_{i}}\right)^{1/\sum _{i=1}^{n}w_{i}}.

The unweighted means correspond to setting all $w i = 1/n$ .

Special cases[edit]

A few particular values of $p$ yield special cases with their own names:^[4]

minimum: $M_{-\infty }(x_{1},\dots ,x_{n})=\lim _{p\to -\infty }M_{p}(x_{1},\dots ,x_{n})=\min\{x_{1},\dots ,x_{n}\}$
A visual depiction of some of the specified cases for $n = 2$ with $a = x 1 = M \infty$ and $b = x 2 = M -\infty$ : harmonic mean, $H = M -1 (a, b)$ , geometric mean, $G = M 0 (a, b)$ arithmetic mean, $A = M 1 (a, b)$ quadratic mean, $Q = M 2 (a, b)$ harmonic mean: $M_{-1}(x_{1},\dots ,x_{n})={\frac {n}{{\frac {1}{x_{1}}}+\dots +{\frac {1}{x_{n}}}}}$
geometric mean $M_{0}(x_{1},\dots ,x_{n})=\lim _{p\to 0}M_{p}(x_{1},\dots ,x_{n})={\sqrt[{n}]{x_{1}\cdot \dots \cdot x_{n}}}$
arithmetic mean: $M_{1}(x_{1},\dots ,x_{n})={\frac {x_{1}+\dots +x_{n}}{n}}$
root mean square or quadratic mean^[5]^[6]: $M_{2}(x_{1},\dots ,x_{n})={\sqrt {\frac {x_{1}^{2}+\dots +x_{n}^{2}}{n}}}$
cubic mean: $M_{3}(x_{1},\dots ,x_{n})={\sqrt[{3}]{\frac {x_{1}^{3}+\dots +x_{n}^{3}}{n}}}$
maximum: $M_{+\infty }(x_{1},\dots ,x_{n})=\lim _{p\to \infty }M_{p}(x_{1},\dots ,x_{n})=\max\{x_{1},\dots ,x_{n}\}$

Proof of ${\textstyle \lim _{p\to 0}M_{p}=M_{0}}$ (geometric mean)

For the purpose of the proof, we will assume without loss of generality that

w_{i}\in [0,1]

w_{i}\in [0,1]

and

\sum _{i=1}^{n}w_{i}=1.

\sum _{i=1}^{n}w_{i}=1.

We can rewrite the definition of $M_{p}$ using the exponential function as

M_{p}(x_{1},\dots ,x_{n})=\exp {\left(\ln {\left[\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\right]}\right)}=\exp {\left({\frac {\ln {\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)}}{p}}\right)}

M_{p}(x_{1},\dots ,x_{n})=\exp {\left(\ln {\left[\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\right]}\right)}=\exp {\left({\frac {\ln {\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)}}{p}}\right)}

In the limit $p \to 0$ , we can apply L'Hôpital's rule to the argument of the exponential function. We assume that $p\in \mathbb {R}$ but $p \neq 0$ , and that the sum of $w i$ is equal to 1 (without loss in generality);^[7] Differentiating the numerator and denominator with respect to $p$ , we have

{\begin{aligned}\lim _{p\to 0}{\frac {\ln {\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)}}{p}}&=\lim _{p\to 0}{\frac {\frac {\sum _{i=1}^{n}w_{i}x_{i}^{p}\ln {x_{i}}}{\sum _{j=1}^{n}w_{j}x_{j}^{p}}}{1}}\\&=\lim _{p\to 0}{\frac {\sum _{i=1}^{n}w_{i}x_{i}^{p}\ln {x_{i}}}{\sum _{j=1}^{n}w_{j}x_{j}^{p}}}\\&={\frac {\sum _{i=1}^{n}w_{i}\ln {x_{i}}}{\sum _{j=1}^{n}w_{j}}}\\&=\sum _{i=1}^{n}w_{i}\ln {x_{i}}\\&=\ln {\left(\prod _{i=1}^{n}x_{i}^{w_{i}}\right)}\end{aligned}}

{\begin{aligned}\lim _{p\to 0}{\frac {\ln {\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)}}{p}}&=\lim _{p\to 0}{\frac {\frac {\sum _{i=1}^{n}w_{i}x_{i}^{p}\ln {x_{i}}}{\sum _{j=1}^{n}w_{j}x_{j}^{p}}}{1}}\\&=\lim _{p\to 0}{\frac {\sum _{i=1}^{n}w_{i}x_{i}^{p}\ln {x_{i}}}{\sum _{j=1}^{n}w_{j}x_{j}^{p}}}\\&={\frac {\sum _{i=1}^{n}w_{i}\ln {x_{i}}}{\sum _{j=1}^{n}w_{j}}}\\&=\sum _{i=1}^{n}w_{i}\ln {x_{i}}\\&=\ln {\left(\prod _{i=1}^{n}x_{i}^{w_{i}}\right)}\end{aligned}}

By the continuity of the exponential function, we can substitute back into the above relation to obtain

\lim _{p\to 0}M_{p}(x_{1},\dots ,x_{n})=\exp {\left(\ln {\left(\prod _{i=1}^{n}x_{i}^{w_{i}}\right)}\right)}=\prod _{i=1}^{n}x_{i}^{w_{i}}=M_{0}(x_{1},\dots ,x_{n})

\lim _{p\to 0}M_{p}(x_{1},\dots ,x_{n})=\exp {\left(\ln {\left(\prod _{i=1}^{n}x_{i}^{w_{i}}\right)}\right)}=\prod _{i=1}^{n}x_{i}^{w_{i}}=M_{0}(x_{1},\dots ,x_{n})

as desired.^[2]

Proof of ${\textstyle \lim _{p\to \infty }M_{p}=M_{\infty }}$ and ${\textstyle \lim _{p\to -\infty }M_{p}=M_{-\infty }}$

Assume (possibly after relabeling and combining terms together) that $x_{1}\geq \dots \geq x_{n}$ . Then

{\begin{aligned}\lim _{p\to \infty }M_{p}(x_{1},\dots ,x_{n})&=\lim _{p\to \infty }\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\\&=x_{1}\lim _{p\to \infty }\left(\sum _{i=1}^{n}w_{i}\left({\frac {x_{i}}{x_{1}}}\right)^{p}\right)^{1/p}\\&=x_{1}=M_{\infty }(x_{1},\dots ,x_{n}).\end{aligned}}

{\begin{aligned}\lim _{p\to \infty }M_{p}(x_{1},\dots ,x_{n})&=\lim _{p\to \infty }\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\\&=x_{1}\lim _{p\to \infty }\left(\sum _{i=1}^{n}w_{i}\left({\frac {x_{i}}{x_{1}}}\right)^{p}\right)^{1/p}\\&=x_{1}=M_{\infty }(x_{1},\dots ,x_{n}).\end{aligned}}

The formula for $M_{-\infty }$ follows from

M_{-\infty }(x_{1},\dots ,x_{n})={\frac {1}{M_{\infty }(1/x_{1},\dots ,1/x_{n})}}=x_{n}.

M_{-\infty }(x_{1},\dots ,x_{n})={\frac {1}{M_{\infty }(1/x_{1},\dots ,1/x_{n})}}=x_{n}.

Properties[edit]

Let $x_{1},\dots ,x_{n}$ be a sequence of positive real numbers, then the following properties hold:^[1]

$\min(x_{1},\dots ,x_{n})\leq M_{p}(x_{1},\dots ,x_{n})\leq \max(x_{1},\dots ,x_{n})$ .
Each generalized mean always lies between the smallest and largest of the $x$ values.
$M_{p}(x_{1},\dots ,x_{n})=M_{p}(P(x_{1},\dots ,x_{n}))$ , where $P$ is a permutation operator.
Each generalized mean is a symmetric function of its arguments; permuting the arguments of a generalized mean does not change its value.
$M_{p}(bx_{1},\dots ,bx_{n})=b\cdot M_{p}(x_{1},\dots ,x_{n})$ .
Like most means, the generalized mean is a homogeneous function of its arguments $x 1, ..., x n$ . That is, if $b$ is a positive real number, then the generalized mean with exponent $p$ of the numbers $b\cdot x_{1},\dots ,b\cdot x_{n}$ is equal to $b$ times the generalized mean of the numbers $x 1, ..., x n$ .
$M_{p}(x_{1},\dots ,x_{n\cdot k})=M_{p}\left[M_{p}(x_{1},\dots ,x_{k}),M_{p}(x_{k+1},\dots ,x_{2\cdot k}),\dots ,M_{p}(x_{(n-1)\cdot k+1},\dots ,x_{n\cdot k})\right]$ .
Like the quasi-arithmetic means, the computation of the mean can be split into computations of equal sized sub-blocks. This enables use of a divide and conquer algorithm to calculate the means, when desirable.

Generalized mean inequality[edit]

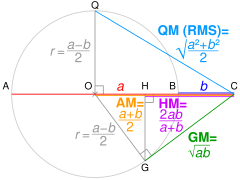
Geometric proof without words that max (a,b) > root mean square (RMS)orquadratic mean (QM) > arithmetic mean (AM) > geometric mean (GM) > harmonic mean (HM) > min (a,b) of two distinct positive numbers a and b ^{[note 1]}

In general, if $p < q$ , then

M_{p}(x_{1},\dots ,x_{n})\leq M_{q}(x_{1},\dots ,x_{n})

M_{p}(x_{1},\dots ,x_{n})\leq M_{q}(x_{1},\dots ,x_{n})

and the two means are equal if and only if

x 1 = x 2 = ... = x n

The inequality is true for real values of $p$ and $q$ , as well as positive and negative infinity values.

It follows from the fact that, for all real $p$ ,

{\frac {\partial }{\partial p}}M_{p}(x_{1},\dots ,x_{n})\geq 0

{\frac {\partial }{\partial p}}M_{p}(x_{1},\dots ,x_{n})\geq 0

which can be proved using Jensen's inequality.

In particular, for $p$ in ${-1, 0, 1}$ , the generalized mean inequality implies the Pythagorean means inequality as well as the inequality of arithmetic and geometric means.

Proof of the weighted inequality[edit]

We will prove the weighted power mean inequality. For the purpose of the proof we will assume the following without loss of generality:

{\begin{aligned}w_{i}\in [0,1]\\\sum _{i=1}^{n}w_{i}=1\end{aligned}}

{\begin{aligned}w_{i}\in [0,1]\\\sum _{i=1}^{n}w_{i}=1\end{aligned}}

The proof for unweighted power means can be easily obtained by substituting $w i = 1/ n$ .

Equivalence of inequalities between means of opposite signs[edit]

Suppose an average between power means with exponents $p$ and $q$ holds:

\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\geq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}

\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\geq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}

applying this, then:

\left(\sum _{i=1}^{n}{\frac {w_{i}}{x_{i}^{p}}}\right)^{1/p}\geq \left(\sum _{i=1}^{n}{\frac {w_{i}}{x_{i}^{q}}}\right)^{1/q}

\left(\sum _{i=1}^{n}{\frac {w_{i}}{x_{i}^{p}}}\right)^{1/p}\geq \left(\sum _{i=1}^{n}{\frac {w_{i}}{x_{i}^{q}}}\right)^{1/q}

We raise both sides to the power of −1 (strictly decreasing function in positive reals):

\left(\sum _{i=1}^{n}w_{i}x_{i}^{-p}\right)^{-1/p}=\left({\frac {1}{\sum _{i=1}^{n}w_{i}{\frac {1}{x_{i}^{p}}}}}\right)^{1/p}\leq \left({\frac {1}{\sum _{i=1}^{n}w_{i}{\frac {1}{x_{i}^{q}}}}}\right)^{1/q}=\left(\sum _{i=1}^{n}w_{i}x_{i}^{-q}\right)^{-1/q}

\left(\sum _{i=1}^{n}w_{i}x_{i}^{-p}\right)^{-1/p}=\left({\frac {1}{\sum _{i=1}^{n}w_{i}{\frac {1}{x_{i}^{p}}}}}\right)^{1/p}\leq \left({\frac {1}{\sum _{i=1}^{n}w_{i}{\frac {1}{x_{i}^{q}}}}}\right)^{1/q}=\left(\sum _{i=1}^{n}w_{i}x_{i}^{-q}\right)^{-1/q}

We get the inequality for means with exponents $- p$ and $- q$ , and we can use the same reasoning backwards, thus proving the inequalities to be equivalent, which will be used in some of the later proofs.

Geometric mean[edit]

For any $q > 0$ and non-negative weights summing to 1, the following inequality holds:

\left(\sum _{i=1}^{n}w_{i}x_{i}^{-q}\right)^{-1/q}\leq \prod _{i=1}^{n}x_{i}^{w_{i}}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}.

\left(\sum _{i=1}^{n}w_{i}x_{i}^{-q}\right)^{-1/q}\leq \prod _{i=1}^{n}x_{i}^{w_{i}}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}.

The proof follows from Jensen's inequality, making use of the fact the logarithm is concave:

\log \prod _{i=1}^{n}x_{i}^{w_{i}}=\sum _{i=1}^{n}w_{i}\log x_{i}\leq \log \sum _{i=1}^{n}w_{i}x_{i}.

\log \prod _{i=1}^{n}x_{i}^{w_{i}}=\sum _{i=1}^{n}w_{i}\log x_{i}\leq \log \sum _{i=1}^{n}w_{i}x_{i}.

By applying the exponential function to both sides and observing that as a strictly increasing function it preserves the sign of the inequality, we get

\prod _{i=1}^{n}x_{i}^{w_{i}}\leq \sum _{i=1}^{n}w_{i}x_{i}.

\prod _{i=1}^{n}x_{i}^{w_{i}}\leq \sum _{i=1}^{n}w_{i}x_{i}.

Taking $q$ -th powers of the $x i$ yields

{\begin{aligned}&\prod _{i=1}^{n}x_{i}^{q{\cdot }w_{i}}\leq \sum _{i=1}^{n}w_{i}x_{i}^{q}\\&\prod _{i=1}^{n}x_{i}^{w_{i}}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}.\end{aligned}}

{\begin{aligned}&\prod _{i=1}^{n}x_{i}^{q{\cdot }w_{i}}\leq \sum _{i=1}^{n}w_{i}x_{i}^{q}\\&\prod _{i=1}^{n}x_{i}^{w_{i}}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}.\end{aligned}}

Thus, we are done for the inequality with positive $q$ ; the case for negatives is identical but for the swapped signs in the last step:

\prod _{i=1}^{n}x_{i}^{-q{\cdot }w_{i}}\leq \sum _{i=1}^{n}w_{i}x_{i}^{-q}.

\prod _{i=1}^{n}x_{i}^{-q{\cdot }w_{i}}\leq \sum _{i=1}^{n}w_{i}x_{i}^{-q}.

Of course, taking each side to the power of a negative number $-1/ q$ swaps the direction of the inequality.

\prod _{i=1}^{n}x_{i}^{w_{i}}\geq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}.

\prod _{i=1}^{n}x_{i}^{w_{i}}\geq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}.

Inequality between any two power means[edit]

We are to prove that for any $p < q$ the following inequality holds:

\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}

\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}

p

is negative, and

q

is positive, the inequality is equivalent to the one proved above:

\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\leq \prod _{i=1}^{n}x_{i}^{w_{i}}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}

\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\leq \prod _{i=1}^{n}x_{i}^{w_{i}}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}

The proof for positive $p$ and $q$ is as follows: Define the following function: $f : R + \to R +$ ${\displaystyle f($ . $f$ is a power function, so it does have a second derivative:

{\displaystyle f''(

f''(x)=\left({\frac {q}{p}}\right)\left({\frac {q}{p}}-1\right)x^{{\frac {q}{p}}-2}

which is strictly positive within the domain of

f

, since

q > p

, so we know

f

is convex.

Using this, and the Jensen's inequality we get:

{\begin{aligned}f\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)&\leq \sum _{i=1}^{n}w_{i}f(x_{i}^{p})\\[3pt]\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{q/p}&\leq \sum _{i=1}^{n}w_{i}x_{i}^{q}\end{aligned}}

{\begin{aligned}f\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)&\leq \sum _{i=1}^{n}w_{i}f(x_{i}^{p})\\[3pt]\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{q/p}&\leq \sum _{i=1}^{n}w_{i}x_{i}^{q}\end{aligned}}

after raising both side to the power of

1/ q

(an increasing function, since

1/ q

is positive) we get the inequality which was to be proven:

\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}

\left(\sum _{i=1}^{n}w_{i}x_{i}^{p}\right)^{1/p}\leq \left(\sum _{i=1}^{n}w_{i}x_{i}^{q}\right)^{1/q}

Using the previously shown equivalence we can prove the inequality for negative $p$ and $q$ by replacing them with $-q$ and $-p$ , respectively.

Generalized f-mean[edit]

The power mean could be generalized further to the generalized $f$ -mean:

M_{f}(x_{1},\dots ,x_{n})=f^{-1}\left({{\frac {1}{n}}\cdot \sum _{i=1}^{n}{f(x_{i})}}\right)

M_{f}(x_{1},\dots ,x_{n})=f^{-1}\left({{\frac {1}{n}}\cdot \sum _{i=1}^{n}{f(x_{i})}}\right)

This covers the geometric mean without using a limit with $f (x) = log(x)$ . The power mean is obtained for $f (x) = x p$ . Properties of these means are studied in de Carvalho (2016).^[3]

Applications[edit]

Signal processing[edit]

A power mean serves a non-linear moving average which is shifted towards small signal values for small $p$ and emphasizes big signal values for big $p$ . Given an efficient implementation of a moving arithmetic mean called smooth one can implement a moving power mean according to the following Haskell code.

powerSmooth :: Floating a => ([a] -> [a]) -> a -> [a] -> [a]
powerSmooth smooth p = map (** recip p) . smooth . map (**p)

For big $p$ it can serve as an envelope detector on a rectified signal.
For small $p$ it can serve as a baseline detector on a mass spectrum.

Notes[edit]

^ If AC = a and BC = b. OC = AMofa and b, and radius r = QO = OG.
Using Pythagoras' theorem, QC² = QO² + OC² ∴ QC = √QO² + OC² = QM.
Using Pythagoras' theorem, OC² = OG² + GC² ∴ GC = √OC² − OG² = GM.
Using similar triangles, HC/GC = GC/OC ∴ HC = GC²/OC = HM.

References[edit]

^ ^a ^b Sýkora, Stanislav (2009). "Mathematical means and averages: basic properties". Stan's Library. III. Castano Primo, Italy: Stan's Library. doi:10.3247/SL3Math09.001.

^ ^a ^b ^c P. S. Bullen: Handbook of Means and Their Inequalities. Dordrecht, Netherlands: Kluwer, 2003, pp. 175-177

^ ^a ^b de Carvalho, Miguel (2016). "Mean, what do you Mean?". The American Statistician. 70 (3): 764‒776. doi:10.1080/00031305.2016.1148632. hdl:20.500.11820/fd7a8991-69a4-4fe5-876f-abcd2957a88c.

^ Weisstein, Eric W. "Power Mean". MathWorld. (retrieved 2019-08-17)

^ Thompson, Sylvanus P. (1965). Calculus Made Easy. Macmillan International Higher Education. p. 185. ISBN 9781349004874. Retrieved 5 July 2020.^{[permanent dead link]}

^ Jones, Alan R. (2018). Probability, Statistics and Other Frightening Stuff. Routledge. p. 48. ISBN 9781351661386. Retrieved 5 July 2020.

^ Handbook of Means and Their Inequalities (Mathematics and Its Applications).

External links[edit]

Retrieved from "https://en.wikipedia.org/w/index.php?title=Generalized_mean&oldid=1225552764" Categories: ●Means ●Inequalities Hidden categories: ●All articles with dead external links ●Articles with dead external links from May 2024 ●Articles with permanently dead external links ●Articles with short description ●Short description matches Wikidata ●Articles needing additional references from June 2020 ●All articles needing additional references ●Articles with example Haskell code ●This page was last edited on 25 May 2024, at 05:31 (UTC). ●Text is available under the Creative Commons Attribution-ShareAlike License 4.0; additional terms may apply. By using this site, you agree to the Terms of Use and Privacy Policy. Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profit organization. ●Privacy policy ●About Wikipedia ●Disclaimers ●Contact Wikipedia ●Code of Conduct ●Developers ●Statistics ●Cookie statement ●Mobile view

●

Contents