ディンキン図形

リー理論という数学の分野において、ディンキン図形︵ディンキンずけい、英: Dynkin diagram︶とは、二重あるいは三重の辺︵二重あるいは三重の線で描かれる︶を持ち得るグラフの一種であり、イェヴゲニ・ディンキン (Евгений Дынкин, Eugene Dynkin) にちなんで名づけられた。多重辺は制約条件により有向である。

ディンキン図形は代数閉体上の半単純リー環を分類する手段として主に興味を持たれている。これはワイル群を生じる、すなわち︵すべてではないが︶多くの有限鏡映群を生じる。ディンキン図形は他の文脈においても現れる。

﹁ディンキン図形﹂という用語には曖昧さがある。ある場合にはディンキン図形は有向であると仮定され、この場合それらはルート系や半単純リー環に対応するが、他の場合には有向でないと仮定され、この場合ワイル群に対応する‥有向図形 B_n, C_nは同じ無向図形を生じ、これは BC_nと呼ばれる。この記事では、﹁ディンキン図形﹂は﹁向き付けられた﹂ディンキン図形を意味し、﹁向き付けられていない﹂ディンキン図形は明示的にそう呼ぶ。

• 
  有限ディンキン図形
• 
  アファイン（拡大）ディンキン図形

半単純リー環の分類

詳細は「半単純リー環#分類」を参照

ディンキン図形の基本的な興味はそれらが代数閉体上の半単純リー環を分類することである。そのようなリー環はそのルート系を通じて分類され、それはディンキン図形によって表せる。そしてディンキン図形は満たさなければならない制約条件によって下記のように分類される。

グラフの辺の向きを落とすことはルート系をそれが生成する有限鏡映群、いわゆるワイル群で置き換えることに対応し、したがって無向ディンキン図形はワイル群を分類する。

関連した分類

ディンキン図形は多くの異なる関係する対象を分類すると解釈でき、表記 "A_n, B_n, ..." は文脈に応じて﹁すべての﹂そのような解釈を指すのに使われる‥この曖昧さは混乱のもととなりうる。

中心的な分類は、単純リー環はルート系を持ち、それに付随して︵有向︶ディンキン図形があることである‥これら3つは全て例えば B_nと呼ばれる。

﹁無﹂向ディンキン図形はコクセター図形の形であり、ワイル群と対応し、これはルート系に付随する有限鏡映群である。したがって B_nは無向図式︵特別な種類のコクセター図式︶、ワイル群︵具体的な鏡映群︶、あるいは抽象的なコクセター群も意味する。

ワイル群は抽象的にコクセター群と同型であるが、同型写像は単純ルートの順序付きの選び方に依存することに注意。ディンキン図形の表記は標準的なものがあるが、コクセター図形・群の表記は様々で、ディンキン図形の表記と一致することもしないこともあることにも注意。

最後に、付随する対象が同じ表記で呼ばれることも﹁時には﹂あるが、これはつねに規則正しくされるわけではない。例えば‥

●ルート系によって生成されるルート格子、例えば E₈格子。これは自然に定義されるが、1対1ではない――例えば、A₂ と G₂はともに六角格子を生成する。

●付随する多胞体――例えば Gosset 4₂₁ polytope は "the E₈ polytope" とも呼ばれる。その頂点は E₈ルート系から生じ、対称変換群として E₈コクセター群を持つからである。

●付随する二次形式あるいは多様体――例えば、E₈ 多様体は E₈格子で与えられる交叉形式を持つ。

これら後者の表記はほとんど例外図形に付随する対象に使われる。古典図形 (A, B, C, D) に付随する対象は代わりに伝統的な名前を持っているのである。

添え字 (n) は、図形の頂点の個数、基底の単純ルートの個数、ルート格子とルート系の線型包の次元、コクセター群の生成元の個数、リー環のランクに等しい。しかしながら、n はリー環の定義加群︵基本表現︶の次元には等しくない――ディンキン図形の添え字をリー環の添え字と混同してはいけない。例えば、B₄ は ${\mathfrak {so}}_{2\cdot 4+1}={\mathfrak {so}}_{9}$${\mathfrak {so}}_{2\cdot 4+1}={\mathfrak {so}}_{9}$に対応し、これは自然に9次元空間に作用するが、リー環としてはランク4をもつ。

Simply laced ディンキン図形は、多重辺を持たないもの (A, D, E) であり、さらに多くの数学的対象を分類する‥ADE分類の議論を参照。

例: A₂

A₂, ルート系。

例えば、記号 A₂は以下を意味する‥

●2つのつながった頂点をもつディンキン図形 , これはコクセター図形とも解釈できる。

●2π/3 (120度) の角度で2つの単純ルートがあるルート系。

●ランク2のリー環 ${\mathfrak {sl}}_{2+1}={\mathfrak {sl}}_{3}.$${\mathfrak {sl}}_{2+1}={\mathfrak {sl}}_{3}.$
●ルートの対称性︵ルートに直交する超平面での鏡映︶のワイル群、︵位数6の︶対称群 S₃に同型。

●生成元と関係式 $\left\langle r_{1},r_{2}\mid (r_{1})^{2}=(r_{2})^{2}=(r_{i}r_{j})^{3}=1\right\rangle$$\left\langle r_{1},r_{2}\mid (r_{1})^{2}=(r_{2})^{2}=(r_{i}r_{j})^{3}=1\right\rangle$によって表示される抽象コクセター群。

制約条件

ディンキン図形はいくつかの制約条件を満たさなければならない；これらは本質的に有限コクセター・ディンキン図形によって満たされるものに結晶的条件を付け加えたものである。

コクセター図形との関係

ディンキン図形は有限コクセター群のコクセター図形と密接に関係し、しばしば同じ用語を使う。

ディンキン図形は有限群のコクセター図形と2つの重要な点において異なる‥

部分的に向き付けられている

ディンキン図形は﹁部分的に向き付けられている﹂――任意の多重辺︵コクセターの用語では "4" 以上でラベル付けられている辺︶は向き付け︵一方の頂点から他方を指す矢印︶を持つ‥したがってディンキン図形は underlying コクセター図形︵無向グラフ︶よりも﹁多くの﹂データを持っている。

ルート系のレベルでは、向き付けは短い方のベクトルに向かって指すことに対応する‥"3" でラベル付けられた辺は向き付けされない、なぜならば対応するベクトルは同じ長さでなければならないからである。︵注意‥著者によってはこの慣習を逆にして矢印が長いベクトルを指すこともある。︶

結晶的制限

ディンキン図形は追加の制限を満たさなければならない、すなわち可能な辺のラベルは 2, 3, 4, 6 のみである。これはコクセター図形は持たない制限で、したがって有限群のすべてのコクセター図形がディンキン図形から来るわけではない。

ルート系のレベルでは、これはルートが格子をなす結晶学的制限定理に対応する。

もう1つの違いは、様式上のものでしかないが、ディンキン図形は伝統的に、辺に "p" とラベル付けずに、︵p = 4, 6 に対して︶二重あるいは三重の辺で描く。

用語﹁ディンキン図形﹂は時には﹁有向﹂グラフを、時に﹁無向﹂グラフを意味する。正確を期すため、この記事では﹁ディンキン図形﹂は﹁有向﹂を意味し、underlying 無向グラフ﹁無向ディンキン図形﹂と呼ぶ。するとディンキン図形とコクセター図形は以下のように関係する‥

	crystallographic	point group
有向	ディンキン図形
無向	無向ディンキン図形	有限群のコクセター図形

これが意味するのは、有限群のコクセター図形は鏡映によって生成される点群に対応し、一方ディンキン図形は結晶学的制限定理に対応する追加の制限を満たさなければならず、また、コクセター図形は無向であるが、一方ディンキン図形は︵部分的に︶有向であることである。

図形によって分類される対応する数学的対象は‥

	crystallographic	point group
有向	ルート系
無向	ワイル群	有限コクセター群

右上の空白は、underlying 無向グラフが︵有限群の︶任意のコクセター図形である有向グラフに対応しており、形式的に定義することはできるが、ほとんど議論されておらず、興味ある数学的対象のことばでの単純な解釈を持たないようである。

上から下への自然な写像――ディンキン図形から無向ディンキン図形へ、あるいはルート系から付随するワイル群へ――と左から右への自然な写像――無向ディンキン図形からコクセター図形へ、あるいはワイル群から有限コクセター群へ――が存在する。

下への写像は︵定義により︶全射であるが、単射ではない、なぜなら B_nと C_nの図形は同じ無向図形に写り、結果のコクセター図形とワイル群はしたがってときどき BC_nと書かれる。

右への写像は単に包含であり――無向ディンキン図形はコクセター図形の特別な場合であり、ワイル群は有限コクセター群の特別な場合である――全射ではない、なぜならばすべてのコクセター図形が無向ディンキン図形ではなく︵抜けている図形は H₃, H₄と p= 5, p≥ 7 に対する I₂(p) である︶、したがってすべての有限コクセター群がワイル群ではないからである。

同型

連結ディンキン図形の例外同型。

ディンキン図形は慣習的にはリストに重複が無いように番号づけられる‥A_n に対しては n≥ 1, B_nに対しては n≥ 2, C_nに対しては n≥ 3, D_nに対しては n≥ 4, そして E_nは n= 6 から始まる。しかしながら族は小さい nに対しても定義でき、図形の例外同型を、そしてリー環と付随するリー群の対応する例外同型を生じる。

明らかに、族を n= 0 あるいは n= 1 から始めることができ、空の図形と頂点が1つの図形はそれぞれ1つずつしかないから、それらはすべて同型である。連結ディンキン図形の他の同型は‥

●$A_{1}\cong B_{1}\cong C_{1}$$A_{1}\cong B_{1}\cong C_{1}$
●$B_{2}\cong C_{2}$$B_{2}\cong C_{2}$
●$D_{2}\cong A_{1}\times A_{1}$$D_{2}\cong A_{1}\times A_{1}$
●$D_{3}\cong A_{3}$$D_{3}\cong A_{3}$
●$E_{3}\cong A_{1}\times A_{2}$$E_{3}\cong A_{1}\times A_{2}$
●$E_{4}\cong A_{4}$$E_{4}\cong A_{4}$
●$E_{5}\cong D_{5}$$E_{5}\cong D_{5}$
これらの同型は単純・半単純リー環の同型に対応し、リー群の同型にも対応する。それらは E_n族に文脈を与えもする。

自己同型

最も対称的なディンキン図形は D₄ であり、これは triality を生じる。

異なる図形の間の同型に加えて、いくつかの図形は自分自身への同型すなわち﹁自己同型﹂も持つ。図形自己同型はリー環の外部自己同型に対応する、つまり、外部自己同型群 Out = Aut/Inn は図形の自己同型の群に等しい。

非自明な自己同型を持つ図形は、A_n (n >1), D_n (n >1), E₆ である。D₄ を除くすべてのこれらの場合において、ただ1つの非自明な自己同型が存在し︵Out = C₂, 位数2の巡回群︶、D₄ に対しては、自己同型群は3文字の対称群︵S₃, 位数6︶である――この現象は“triality”と呼ばれる。すべてのこれらの図形自己同型が、図形がどのように平面に慣習的に描かれるかのユークリッド対称性として実現できるということは起こるが、これはそれらがどのように描かれるかの人工物に過ぎず、内在的な構造ではない。

A_n.

A_n に対して、図形の自己同型は直線状の図形の反転である。図形の頂点は基本ウェイトを添え字付け、これらは︵A_n−1 に対して︶i = 1, ..., nに対して $\bigwedge ^{i}C^{n}$$\bigwedge ^{i}C^{n}$であり、図形の自己同型は duality $\bigwedge ^{i}C^{n}\mapsto \bigwedge ^{n-i}C^{n}$$\bigwedge ^{i}C^{n}\mapsto \bigwedge ^{n-i}C^{n}$に対応する。リー環 ${\mathfrak {sl}}_{n+1}$${\mathfrak {sl}}_{n+1}$として実現すると、外部自己同型は負の転置 $T\mapsto -T^{\mathrm {T} }$$T\mapsto -T^{\mathrm {T} }$として表現でき、これは双対表現の作用の仕方である。

D_n.

D_n に対して、図形の自己同型はY字の端の2つの頂点の入れ替えで、2つの chiral スピン表現を入れ替えることに対応する。リー環 ${\mathfrak {so}}_{2n}$${\mathfrak {so}}_{2n}$として実現して、外部自己同型は O(2n) の行列式 −1 の行列による共役として表せる。$\mathrm {A} _{3}\cong \mathrm {D} _{3}$$\mathrm {A} _{3}\cong \mathrm {D} _{3}$ であるから、それらの自己同型は一致し、$\mathrm {D} _{2}\cong \mathrm {A} _{1}\times \mathrm {A} _{1}$$\mathrm {D} _{2}\cong \mathrm {A} _{1}\times \mathrm {A} _{1}$ は不連結で、自己同型は2つの頂点を入れ替えることに対応する。

D₄ に対して、基本表現は2つのスピン表現に同型であり、結果の3文字の対称群︵S₃, あるいは位数6の二面体群 Dih₃︶はリー環の自己同型と図形の自己同型の両方に対応する。

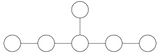
E₆.

E₆ の自己同型群は図形を反転させることに対応し、ヨルダン代数を用いて表せる。

不連結な図形は、﹁半﹂単純リー環に対応し、図形の成分の交換から来る自己同型を持つかもしれない。

標数2では、F₄ の矢印は無視でき、追加の図形の自己同型と対応する鈴木・リ群を生じる。

正標数では、追加の﹁図形自己同型﹂が存在する――粗く言えば、標数 pでは図形の自己同型を取るときにディンキン図形の重複度 pの結合の矢印を無視できることがある。したがって標数2では $\mathrm {B} _{2}\cong \mathrm {C} _{2}$$\mathrm {B} _{2}\cong \mathrm {C} _{2}$とF₄ の位数2の自己同型があり、標数3ではG₂ の位数2の自己同型がある。しかしすべての状況で適用するわけではない‥例えば、そのような自己同型は対応する代数群の自己同型として生じるとは限らず、有限体に値を持つ点のレベルでである。

図形の自己同型を通したリー群の構成

図形の自己同型は追加のリー群やリー型の群を生じ、これは有限単純群の分類において中心的に重要な群である。

ディンキン図形のことばでのリー群のシュバレー群構成は古典群のいくつか、すなわちユニタリ群と非分裂直交群を生み出さない。Steinberg 群はユニタリ群 ²A_nを構成し、他の直交群は ²D_nとして構成される、ただしどちらの場合においてもこれは図形自己同型を体自己同型と組み合わせることが必要である。これはまた追加の exotic リー群 ²E₆と ³D₄も生じ、後者は位数3の自己同型を持つ体上でしか定義されない。

正標数における追加の図形自己同型は鈴木・リ群 ²B₂, ²F₄, ²G₂を生じる。

Folding

有限コクセター群の foldings.

アファイン・コクセター群の foldings, 3つの名前の慣習を添えて：第一に、もともとの拡大された集合；第二は箙のグラフの文脈で用いられる；最後はヴィクトル・カッツによって twisted アファイン・リー環のために。

(Simply-laced) ディンキン図形︵有限あるいはアファイン︶で︵下記の1つの条件を満たす︶対称性を持つものは、その対称性によって割ることができ、新しい、一般には multiply laced な図形が得られ、この過程を folding (“折り畳み”) と呼ぶ︵ほとんどの対称性は 2-fold であるため︶。リー環のレベルでは、これは外部自己同型群で不変な部分環を取ることに対応し、過程は図形を用いることなしに純粋にルート系を参照して定義できる。さらに、すべての multiply laced 図形︵有限あるいは無限︶は simply-laced 図形を folding して得ることができる。

Folding が可能なための自己同型についての1つの条件は、︵自己同型の下での︶同じ軌道にあるグラフの相異なる頂点が辺で結ばれてはいけないことである‥ルート系のレベルでは、同じ軌道にあるルートは直交していなければならない。図形のレベルでは、これは必要である、なぜならばそうでないと商図形が、2つの頂点を同一視するがそれらの間に辺があるためにループを持つが、ループはディンキン図形では許されていないからである。

商 ("folded") 図形の頂点と辺はもとの図形の頂点と辺の軌道である‥︵とりわけ原子価が2よりも大きい頂点において︶2つの入射する辺が同じ辺に写る場合を除いて、辺は1本であり、写像の“分岐点”における重みは入射する辺の個数で、矢印は入射する頂点﹁を﹂指し、“分岐点は non-homogeneous point に写る”。例えば、D₄ を G₂に folding すると、G₂ の辺は、3つの外側の頂点︵原子価1︶の類から中心の頂点︵原子価3︶の類に向かう。

有限図形の foldings は以下である‥

●A_2n − 1 → C_n

︵A_2n の自己同型は folding を生じない、なぜならば真ん中の2つの頂点は辺で結ばれているが、同じ軌道にあるからである。︶

●D_n + 1 → B_n

●D₄ → G₂ (if quotienting by the full group or a 3-cycle, in addition to $D_{4}\to B_{3}$$D_{4}\to B_{3}$in 3 different ways, if quotienting by an involution)

●E₆ → F₄

アファイン図形に対して類似の foldings が存在する、例えば‥

●${\tilde {A}}_{2n-1}\to {\tilde {C}}_{n}$${\tilde {A}}_{2n-1}\to {\tilde {C}}_{n}$
●${\tilde {D}}_{n+1}\to {\tilde {B}}_{n}$${\tilde {D}}_{n+1}\to {\tilde {B}}_{n}$
●${\tilde {D}}_{4}\to {\tilde {G}}_{2}$${\tilde {D}}_{4}\to {\tilde {G}}_{2}$
●${\tilde {E}}_{6}\to {\tilde {F}}_{4}$${\tilde {E}}_{6}\to {\tilde {F}}_{4}$
Foldings の概念はより一般にコクセター図形にも適用できる――特に、ディンキン図形の許される商を H_nと I₂(p) に一般化できる。幾何学的にはこれは uniform polytope の射影に対応する。特に、任意の simply laced ディンキン図形は I₂(h) に fold できる、ただし hはコクセター数で、幾何学的にはコクセター平面への射影に対応する。

Folding は︵半単純︶リー環についての問題を simply-laced なものと自己同型についての問題に還元でき、これは multiply laced リー環を直接扱うよりも単純かもしれない‥これは例えば半単純リー環を構成する際にすることができる。さらなる議論は Math Overflow: Folding by Automorphisms を参照。

図形の他の写像

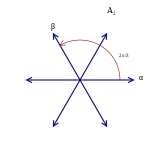A2 ルート系

G2 ルート系

図形のいくつかの追加の写像は以下に詳述するように意味のある解釈を持つ。しかしながら、ルート系のすべての写像が図形の写像として生じるわけではない。

例えば、A₂ のG₂ へのルート系の包含は2つあり、1つは6つの長いルートへの、もう1つは6つの短いルートへの写像である。しかしながら、G₂ 図形の2つの頂点は、1つは長いルートに、もう1つは短いルートに対応するが、A₂ 図形の頂点は等しい長さのルートに対応するから、ルート系のこの写像は図形の写像としては表せない。

ルート系のある包含は1つの図形の別の図形の誘導部分グラフ、すなわち﹁頂点は部分集合で、辺はそれらの間の全て﹂と表せる。なぜならば、ディンキン図形から頂点を取り除くことはルート系から単純ルートを取り除くことに対応し、これは階数が1小さいルート系になるからである。対照的に、頂点は変えずに辺を取り除くこと︵あるいは辺の重複度を変えること︶はルート間の角度を変えることに対応し、これはルート系全体を変えずにはできない。したがって、意味があるように頂点を取り除くことはできるが、辺ではできない。連結図形から頂点を取り除くと、頂点が葉ならば連結図形︵単純リー環︶になり、あるいは、2つか3つの成分からなる不連結図形︵半単純だが単純でないリー環︶になるかもしれない︵後者は D_nと E_nに対して︶。リー環のレベルでは、これらの包含は部分リー環に対応する。

極大部分グラフは以下のようである‥図形の自己同型によって関連する部分グラフは "conjugate" とラベル付けられている‥

●A_n+1: A_n, in 2 conjugate ways.

●B_n+1: A_n, B_n.

●C_n+1: A_n, C_n.

●D_n+1: A_n (2 conjugate ways), D_n.

●E_n+1: A_n, D_n, E_n.
●For E₆, two of these coincide: $\mathrm {D} _{5}\cong \mathrm {E} _{5}$$\mathrm {D} _{5}\cong \mathrm {E} _{5}$and are conjugate.

●F₄: B₃, C₃.

●G₂: A₁, in 2 non-conjugate ways (as a long root or a short root).

最後に、図式の双対性は、存在すれば、矢印の向きの反転に対応する‥B_n と C_nは双対であり、F₄ や G₂や simply-laced ADE 図形は自己双対である。

Simply laced

詳細は「ADE分類」を参照

Simply laced ディンキン図形は多様な数学的対象を分類する；これは ADE 分類と呼ばれる。

多重辺を持たないディンキン図形、および対応するリー環やリー群は、simply laced と呼ばれる。これらは A_n, D_n, E_n 図形であり、そのような図形が分類する現象は ADE 分類と呼ばれる。この場合ディンキン図形は、多重辺を持たないから、コクセター図形とちょうど一致する。

佐武図形

詳細は「佐武図形」を参照

ディンキン図形は﹁複素﹂半単純リー環を分類する。実半単純リー環は複素半単純リー環の実形として分類でき、これらは佐武図形によって分類され、これらはディンキン図形から、あるルールに従って、いくつかの頂点を黒でラベル付け、いくつかの他の頂点を対で矢印で結ぶことによって、得られる。

歴史

「半単純リー環#歴史」も参照

イェヴゲニ・ディンキン。

ディンキン図形はイェヴゲニ・ディンキンに因んで名づけられており、彼はそれを2つの論文 (1946, 1947) で用いて、半単純リー環の分類を簡素化した‥(Dynkin 2000) を参照。ディンキンがソビエト連邦を1976年に去った時、当時それは反逆と同等と考えられており、ソビエトの数学者は彼の名前を用いずに﹁単純ルートの図形﹂と呼ぶよう指示された。

無向グラフは早くにコクセター (1934) によって鏡映群を分類するために用いられていた、ここで頂点は単純鏡映に対応する‥グラフはヴィット (1941) によって︵長さの情報とともに︶ルート系に関連して頂点が単純ルートと対応するよう今日用いられているように用いられた。ディンキンはそれらを1946年と1947年に用い、1947年の論文でコクセターとヴィットに謝意を表した。

慣習

ディンキン図形はいくつかの方法で描かれる‥ここで従う慣習は一般的で、価数2の頂点の角度は 180° で、D_n の価数3の頂点の角度は 120° で、E_n の価数3の頂点の角度は 90°/90°/180° で、多重度は 1, 2, 3 本の平行な辺で表され、ルートの長さは辺に向き付けの矢印を描くことで表す。簡単のためだけではなく、この慣習のさらなる利点は、図形自己同型が図形のユークリッド等長同型によって実現されることである。

別の慣習には、多重度を表すのに辺のそばに数を書くもの︵コクセター図形で一般に用いられる︶、ルート長を表すのに頂点を黒く塗るもの、価数2の頂点の角度を 120° にして頂点をより異ならせるものがある。

頂点の番号付けにも慣習がある。最も一般的な現代の慣習は1960年代に発展し、(Bourbaki 1968) に描かれている。

階数 2 のディンキン図形

ディンキン図形は一般カルタン行列と同値である。階数2のディンキン図形を対応する 2 × 2 カルタン行列とともに書いたこの表に示されているように。

階数2のときは、カルタン行列の形は

$A={\begin{bmatrix}2&a_{12}\\a_{21}&2\end{bmatrix}}$$A={\begin{bmatrix}2&a_{12}\\a_{21}&2\end{bmatrix}}$
である。多重辺図形はカルタン行列の非対角成分 −a₂₁, −a₁₂ に対応し、描かれる辺の個数は max(−a₂₁, −a₁₂) に等しく、矢印は −1 でない元を指している。

一般カルタン行列は正方行列 A= (a_ij) であって以下を満たすものである‥

(一)対角成分に対して、a_ii = 2.

(二)非対角成分に対して、a_ij ≤ 0.

(三)a_ij = 0 ⇔ a_ji= 0.

一般カルタン行列は群が有限型であるか︵それが正定値行列のとき、すなわちすべての固有値が正のとき︶、アファイン型であるか︵それが正定値ではないが、半正定値であるとき、すなわちすべての固有値が非負のとき︶、不定値型であるかを決定する。不定値型はしばしばさらに細分化され、例えばコクセター群がローレンツ型であるとは、それが1つの負の固有値を持ち全ての他の固有値は正であることをいう。さらに、複数の文献が双曲型コクセター群に言及しているが、この用語にはいくつかの同値でない定義がある。以下の議論では、双曲型コクセター群はローレンツ型の特別な場合で、ある追加の条件を満たすものである。階数2に対しては、行列式が負のすべてのカルタン行列は双曲型コクセター群に対応することに注意。しかし一般には、行列式が負のほとんどの行列は双曲型でもローレンツでもない。

︵連結︶有限型は (−a₂₁, −a₁₂) = (1, 1), (2, 1), (3, 1) で、アファイン型︵行列式 0︶は (−a₂₁, −a₁₂) = (2, 2), (4, 1) である。

階数 2 のディンキン図形

グループ の名前	ディンキン図形			カルタン行列		対称性 の位数	関連する simply-laced 群3
	（標準） 多重辺 グラフ	値付き グラフ1	コクセター グラフ2	${\begin{bmatrix}2&a_{12}\\a_{21}&2\end{bmatrix}}$	行列式 (4 − a21a12)
有限 (行列式 > 0)
A1 × A1				$\left[{\begin{smallmatrix}2&0\\0&2\end{smallmatrix}}\right]$	4	2
A2 （無向）				$\left[{\begin{smallmatrix}2&-1\\-1&2\end{smallmatrix}}\right]$	3	3
B2				$\left[{\begin{smallmatrix}2&-2\\-1&2\end{smallmatrix}}\right]$	2	4	A3
C2				$\left[{\begin{smallmatrix}2&-1\\-2&2\end{smallmatrix}}\right]$	2	4	A3
BC2 （無向）				$\left[{\begin{smallmatrix}2&-{\sqrt {2}}\\-{\sqrt {2}}&2\end{smallmatrix}}\right]$	2	4
G2				$\left[{\begin{smallmatrix}2&-1\\-3&2\end{smallmatrix}}\right]$	1	6	D4
G2 （無向）				$\left[{\begin{smallmatrix}2&-{\sqrt {3}}\\-{\sqrt {3}}&2\end{smallmatrix}}\right]$	1	6
アファイン (行列式 = 0)
A(1) 1				$\left[{\begin{smallmatrix}2&-2\\-2&2\end{smallmatrix}}\right]$	0	∞	${\tilde {A}}_{3}$
A(2) 2				$\left[{\begin{smallmatrix}2&-1\\-4&2\end{smallmatrix}}\right]$	0	∞	${\tilde {D}}_{4}$
双曲 (行列式 < 0)
				$\left[{\begin{smallmatrix}2&-1\\-5&2\end{smallmatrix}}\right]$	−1	-
				$\left[{\begin{smallmatrix}2&-2\\-3&2\end{smallmatrix}}\right]$	−2	-
				$\left[{\begin{smallmatrix}2&-1\\-6&2\end{smallmatrix}}\right]$	−2	-
				$\left[{\begin{smallmatrix}2&-1\\-7&2\end{smallmatrix}}\right]$	−3	-
				$\left[{\begin{smallmatrix}2&-2\\-4&2\end{smallmatrix}}\right]$	−4	-
				$\left[{\begin{smallmatrix}2&-1\\-8&2\end{smallmatrix}}\right]$	−4	-
				$\left[{\begin{smallmatrix}2&-3\\-3&2\end{smallmatrix}}\right]$	−5	-
				$\left[{\begin{smallmatrix}2&-b\\-a&2\end{smallmatrix}}\right]$	4 − ab < 0	-
注1: 双曲群 (a12a21>4) に対して、多重辺スタイルは捨てて、辺上の明示的なラベル付け (a21, a12) を選んだ。これらは通常有限およびアファイングラフには適用されない。 注2: 無向群に対して、コクセター図形は交換可能である。それらは通常、対称性の位数によってラベル付けされ、位数3はラベルを付けない。 注3: 多くの多重辺群は適切な folding operation を施すことによって階数の高い simply-laced 群から得られる。

有限ディンキン図形

頂点が 1 から 9 の有限ディンキン図形

階数	古典型リー群				例外型リー群
	A1+	B2+	C2+	D2+	E3–8	G2 / F4
1	A1
2	A2	B2	C2 = B2	D2 = A1xA1		G2
3	A3	B3	C3	D3 = A3	E3 = A2xA1
4	A4	B4	C4	D4	E4 = A4	F4
5	A5	B5	C5	D5	E5 = D5
6	A6	B6	C6	D6	E6
7	A7	B7	C7	D7	E7
8	A8	B8	C8	D8	E8
9	A9	B9	C9	D9
10+	..	..	..	..

アファインディンキン図形

詳細は「アファインルート系」を参照

ディンキン図形の拡張、すなわちアファインディンキン図形が存在する‥これらはアファインリー環のカルタン行列を分類する。これらは (Kac 1994, Chapter 4, pp. 47–) において分類され、特に (Kac 1994, pp. 53–55) にリストされている。アファイン図形は X(1)
l , X(2)
l , X(3)
l  と書かれる、ただし Xは対応する有限図形の文字で、指数はアファイン図形のどの列にそれらが入っているかに依存する。これらの第一、X(1)
l  は、もっとも一般的で、拡大ディンキン図形 (extended Dynkin diagram) と呼ばれ、チルダで表され、時には右上に + の記号をつけることもある、例えば ${\displaystyle {\tilde {A}}_{5}=A_{5}^{($1)}=A_{5}^{+}} ${\tilde {A}}_{5}=A_{5}^{(1)}=A_{5}^{+}$のように。(2) と (3) の列は twisted アファイン図形と呼ばれる。

図形については Dynkin diagram generator を参照。

拡大ディンキン図形の集合、追加の頂点は緑（Bn に対しては n ≥ 3, Dn に対しては n ≥ 4）

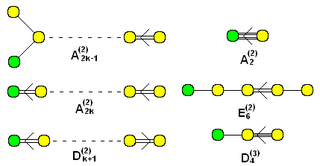"Twisted" アファイン形は (2) あるいは (3) の上付き添え字で名づけられる。 （k はグラフの黄色の頂点の個数）

以下が頂点の個数が10個までのアファイン群に対するディンキングラフのすべてである。拡大ディンキングラフは、上の有限グラフに1つの頂点を加えた ~ 族として与えられる。他の有向グラフの変種は、位数の高い群の folding を表す値が (2) か (3) の上付き添え字とともに与えられる。これらは ﹁twistedアファイン﹂図形とカテゴライズされる。

頂点が 2 から 10 までの連結アファインディンキングラフ
（無向グラフでグループ分けしている）

階数	${\tilde {A}}_{1+}$	${\tilde {B}}_{3+}$	${\tilde {C}}_{2+}$	${\tilde {D}}_{4+}$	E / F / G
2	${\tilde {A}}_{1}$ or ${A}_{1}^{(1)}$		${A}_{2}^{(2)}$:
3	${\tilde {A}}_{2}$ or ${A}_{2}^{(1)}$		${\tilde {C}}_{2}$ or ${C}_{2}^{(1)}$ ${D}_{5}^{(2)}$: ${A}_{4}^{(2)}$:		${\tilde {G}}_{2}$ or ${G}_{2}^{(1)}$ ${D}_{4}^{(3)}$
4	${\tilde {A}}_{3}$ or ${A}_{3}^{(1)}$	${\tilde {B}}_{3}$ or ${B}_{3}^{(1)}$ ${A}_{5}^{(2)}$:	${\tilde {C}}_{3}$ or ${C}_{3}^{(1)}$ ${D}_{6}^{(2)}$: ${A}_{6}^{(2)}$:
5	${\tilde {A}}_{4}$ or ${A}_{4}^{(1)}$	${\tilde {B}}_{4}$ or ${B}_{4}^{(1)}$ ${A}_{7}^{(2)}$:	${\tilde {C}}_{4}$ or ${C}_{4}^{(1)}$ ${D}_{7}^{(2)}$: ${A}_{8}^{(2)}$:	${\tilde {D}}_{4}$ or ${D}_{4}^{(1)}$	${\tilde {F}}_{4}$ or ${F}_{4}^{(1)}$ ${E}_{6}^{(2)}$
6	${\tilde {A}}_{5}$ or ${A}_{5}^{(1)}$	${\tilde {B}}_{5}$ or ${B}_{5}^{(1)}$ ${A}_{9}^{(2)}$:	${\tilde {C}}_{5}$ or ${C}_{5}^{(1)}$ ${D}_{8}^{(2)}$: ${A}_{10}^{(2)}$:	${\tilde {D}}_{5}$ or ${D}_{5}^{(1)}$
7	${\tilde {A}}_{6}$ or ${A}_{6}^{(1)}$	${\tilde {B}}_{6}$ or ${B}_{6}^{(1)}$ ${A}_{11}^{(2)}$:	${\tilde {C}}_{6}$ or ${C}_{6}^{(1)}$ ${D}_{9}^{(2)}$: ${A}_{12}^{(2)}$:	${\tilde {D}}_{6}$ or ${D}_{6}^{(1)}$	${\tilde {E}}_{6}$ or ${E}_{6}^{(1)}$
8	${\tilde {A}}_{7}$ or ${A}_{7}^{(1)}$	${\tilde {B}}_{7}$ or ${B}_{7}^{(1)}$ ${A}_{13}^{(2)}$:	${\tilde {C}}_{7}$ or ${C}_{7}^{(1)}$ ${D}_{10}^{(2)}$: ${A}_{14}^{(2)}$:	${\tilde {D}}_{7}$ or ${D}_{7}^{(1)}$	${\tilde {E}}_{7}$ or ${E}_{7}^{(1)}$
9	${\tilde {A}}_{8}$ or ${A}_{8}^{(1)}$	${\tilde {B}}_{8}$ or ${B}_{8}^{(1)}$ ${A}_{15}^{(2)}$:	${\tilde {C}}_{8}$ or ${C}_{8}^{(1)}$ ${D}_{11}^{(2)}$: ${A}_{16}^{(2)}$:	${\tilde {D}}_{8}$ or ${D}_{8}^{(1)}$	${\tilde {E}}_{8}$ or ${E}_{8}^{(1)}$
10	${\tilde {A}}_{9}$ or ${A}_{9}^{(1)}$	${\tilde {B}}_{9}$ or ${B}_{9}^{(1)}$ ${A}_{17}^{(2)}$:	${\tilde {C}}_{9}$ or ${C}_{9}^{(1)}$ ${D}_{12}^{(2)}$: ${A}_{18}^{(2)}$:	${\tilde {D}}_{9}$ or ${D}_{9}^{(1)}$
11	...	...	...	...

双曲型および高次のディンキン図形

コンパクトおよび非コンパクトな双曲ディンキングラフはすべて列挙されている。階数 3 の双曲グラフはすべてコンパクトである。コンパクト双曲ディンキン図形は階数 5 まで存在し、非コンパクト双曲グラフは階数 10 まで存在する。

要約

階数	コンパクト	非コンパクト	計
3	31	93	123
4	3	50	53
5	1	21	22
6	0	22	22
7	0	4	4
8	0	5	5
9	0	5	5
10	0	4	4

コンパクト双曲ディンキン図形

コンパクト双曲グラフ

階数 3		階数 4	階数 5
線型グラフ (6 4 2): H100(3): H101(3): H105(3): H106(3): (6 6 2): H114(3): H115(3): H116(3):	巡回グラフ (4 3 3): H1(3): (4 4 3): 3 forms... (4 4 4): 2 forms... (6 3 3): H3(3): (6 4 3): 4 forms... (6 4 4): 4 forms... (6 6 3): 3 forms... (6 6 4): 4 forms... (6 6 6): 2 forms...	(4 3 3 3): H8(4): H13(4): (4 3 4 3): H14(4):	(4 3 3 3 3): H7(5):

非コンパクト (Over-extended forms)

M理論のように理論物理学において用いられるいくつかの表記は拡大群に対し "~" の代わりに "+" の上付き添え字を用い、これにより higher extensions groups が定義できる。

(一)Extended ディンキン図形︵アファイン︶は "+" で与えられ1つの付け加えられた頂点を表す︵"~" と同じ︶。

(二)Over-extended ディンキン図形︵双曲︶は "^" あるいは "++" で与えられ、2つの付け加えられた頂点を表す。

(三)Very-extended ディンキン図形で3つの頂点が付け加えられたものは "+++" で与えられる。

Over-extended（双曲）ディンキン図形のいくつかの例

階数	AEn = An−2(1)^	BEn = Bn−2(1)^ CEn	Cn−2(1)^	DEn = Dn−2(1)^	E / F / G
3	AE3:
4	AE4:		C2(1)^ A4(2)'^ A4(2)^ D3(2)^		G2(1)^ D4(3)^
5	AE5:	BE5 CE5	C3(1)^ A6(2)^ A6(2)'^ D5(2)^
6	AE6	BE6 CE6	C4(1)^ A8(2)^ A8(2)'^ D7(2)^	DE6	F4(1)^ E6(2)^
7	AE7	BE7 CE7		DE7
8	AE8	BE8 CE8		DE8	E6(1)^
9	AE9	BE9 CE9		DE9	E7(1)^
10		BE10 CE10		DE10	E10 = E8(1)^

238個の双曲群（コンパクト・非コンパクト）

階数 n ≥ 3 の238個の（コンパクトおよび非コンパクト）双曲群は H(n)
i  と名付けられ、各階数に対して i = 1, 2, 3, ... とリストされている。

Very-extended

Very-extended 群はローレンツ群であり、有限群に3つの頂点を加えることで定義される。E₈, E₇, E₆, F₄, G₂ は very-extended 群で終わる6つの列を提供する。示されていない他の extended series は各 nに対して異なる列としてA_n, B_n, C_n, D_n から定義できる。付随するカルタン行列の行列式は列がどこで有限︵正︶からアファイン︵零︶から非コンパクト双曲群︵負︶に変わるかを決定し、1つの時間的次元を用いて定義できるローレンツ群として終わり、M理論において用いられる。

階数 2 の extended series

有限	A2	C2	G2
2	A2	C2	G2
3	A2+=${\tilde {A}}_{2}$	C2+=${\tilde {C}}_{2}$	G2+=${\tilde {G}}_{2}$
4	A2++	C2++	G2++
5	A2+++	C2+++	G2+++
Det(Mn)	3(3 − n)	2(3 − n)	3 − n

階数 3 と 4 の extended series

有限	A3	B3	C3	A4	B4	C4	D4	F4
2		A12						A2
3	A3	B3	C3		B2A1		A13
4	A3+=${\tilde {A}}_{3}$	B3+=${\tilde {B}}_{3}$	C3+=${\tilde {C}}_{3}$	A4	B4	C4	D4	F4
5	A3++	B3++	C3++	A4+=${\tilde {A}}_{4}$	B4+=${\tilde {B}}_{4}$	C4+=${\tilde {C}}_{4}$	D4+=${\tilde {D}}_{4}$	F4+=${\tilde {F}}_{4}$
6	A3+++	B3+++	C3+++	A4++	B4++	C4++	D4++	F4++
7				A4+++	B4+++	C4+++	D4+++	F4+++
Det(Mn)	4(4 − n)	2(4 − n)		5(5 − n)	2(5 − n)		4(5 − n)	5 − n

階数 5 と 6 の extended series

有限	A5	B5	D5	A6	B6	D6	E6
4		B3A1	A3A1				A22
5	A5		D5		B4A1	D4A1	A5
6	A5+=${\tilde {A}}_{5}$	B5+=${\tilde {B}}_{5}$	D5+=${\tilde {D}}_{5}$	A6	B6	D6	E6
7	A5++	B5++	D5++	A6+=${\tilde {A}}_{6}$	B6+=${\tilde {B}}_{6}$	D6+=${\tilde {D}}_{6}$	E6+=${\tilde {E}}_{6}$
8	A5+++	B5+++	D5+++	A6++	B6++	D6++	E6++
9				A6+++	B6+++	D6+++	E6+++
Det(Mn)	6(6 − n)	2(6 − n)	4(6 − n)	7(7 − n)	2(7 − n)	4(7 − n)	3(7 − n)

階数 7 以上のいくつかの extended series

有限	A7	B7	D7	E7	E8
3					E3=A2A1
4				A3A1	E4=A4
5				A5	E5=D5
6		B5A1	D5A1	D6	E6
7	A7	B7	D7	E7	E7
8	A7+=${\tilde {A}}_{7}$	B7+=${\tilde {B}}_{7}$	D7+=${\tilde {D}}_{7}$	E7+=${\tilde {E}}_{7}$	E8
9	A7++	B7++	D7++	E7++	E9=E8+=${\tilde {E}}_{8}$
10	A7+++	B7+++	D7+++	E7+++	E10=E8++
11					E11=E8+++
Det(Mn)	8(8 − n)	2(8 − n)	4(8 − n)	2(8 − n)	9 − n

関連項目

• 佐武図形
• ウィキブックス Klassifikation von Wurzelsystemen (ルート系の分類) （ドイツ語）

参考文献

• Dynkin, E. B. (1947), “The structure of semi-simple algebras .” (ロシア語), Uspehi Matem. Nauk, (N.S.) 2 (4(20)): 59–127 
• Bourbaki, Nicolas (1968), “Chapters 4–6”, Groupes et algebres de Lie, Paris: Hermann 
• Jacobson, Nathan (1971-06-01), Exceptional Lie Algebras (1 ed.), CRC Press, ISBN 0-8247-1326-5 
• Humphreys, James E. (1972), Introduction to Lie Algebras and Representation Theory, Birkhäuser, ISBN 978-0-387-90053-7 
• Fulton, William; Harris, Joe (1991), Representation theory. A first course, Graduate Texts in Mathematics, Readings in Mathematics, 129, New York: Springer-Verlag, ISBN 978-0-387-97495-8, MR1153249, ISBN 978-0-387-97527-6 
• Dynkin, Evgeniĭ Borisovich; Alexander Adolph Yushkevich; Gary M. Seitz; A. L. Onishchik (2000), Selected papers of E.B. Dynkin with commentary, AMS Bookstore, ISBN 978-0-8218-1065-1 
• Knapp, Anthony W. (2002), Lie groups beyond an introduction (2nd ed.), Birkhäuser, ISBN 978-0-8176-4259-4 
• Stekolshchik, R. (2008), Notes on Coxeter Transformations and the McKay Correspondence, Springer Monographs in Mathematics, doi:10.1007/978-3-540-77398-3, ISBN 978-3-540-77398-6 

外部リンク

• Dynkin diagram at Encyclopaedia of Mathematics
• John Baez on the ubiquity of Dynkin diagrams in mathematics
• Web tool for making publication-quality Dynkin diagrams with labels (written in JavaScript)