

Harmonic analysis is a branch of mathematics concerned with investigating the connections between a function and its representation in frequency. The frequency representation is found by using the Fourier transform for functions on the real line or by Fourier series for periodic functions. Generalizing these transforms to other domains is generally called Fourier analysis, although the term is sometimes used interchangeably with harmonic analysis. Harmonic analysis has become a vast subject with applications in areas as diverse as number theory, representation theory, signal processing, quantum mechanics, tidal analysis and neuroscience.
The term "harmonics" originated as the Ancient Greek word harmonikos, meaning "skilled in music".[1] In physical eigenvalue problems, it began to mean waves whose frequencies are integer multiples of one another, as are the frequencies of the harmonics of music notes. Still, the term has been generalized beyond its original meaning.
Historically Harmonic functions were the solutions of Laplace equation,[2] this concept was extended first to special functions,[3] then to general elliptic operators[4] and nowadays harmonic functions are considered as a generalization of periodic functions[5]onfunction spaces defined on a manifold, for example as solutions of general, not necessarly elliptic, partial differential equations including some boundary conditions that may drive their symmetry or periodicity.[6]
The classical Fourier transform on Rn is still an area of ongoing research, particularly concerning Fourier transformation on more general objects such as tempered distributions. For instance, if we impose some requirements on a distribution f, we can attempt to translate these requirements into the Fourier transform of f. The Paley–Wiener theorem is an example. The Paley–Wiener theorem immediately implies that if f is a nonzero distributionofcompact support (these include functions of compact support), then its Fourier transform is never compactly supported (i.e., if a signal is limited in one domain, it is unlimited in the other). This is an elementary form of an uncertainty principle in a harmonic-analysis setting.
Fourier series can be conveniently studied in the context of Hilbert spaces, which provides a connection between harmonic analysis and functional analysis. There are four versions of the Fourier transform, dependent on the spaces that are mapped by the transformation:
Abstract harmonic analysis is primarily concerned with how real or complex-valued functions (often on very general domains) can be studied using symmetries such as translationsorrotations (for instance via the Fourier transform and its relatives); this field is of course related to real-variable harmonic analysis, but is perhaps closer in spirit to representation theory and functional analysis.[7]
One of the most modern branches of harmonic analysis, having its roots in the mid-20th century, is analysisontopological groups. The core motivating ideas are the various Fourier transforms, which can be generalized to a transform of functions defined on Hausdorff locally compact topological groups.[8]
One of the major results in the theory of functions on abelian locally compact groups is called Pontryagin duality. Harmonic analysis studies the properties of that duality. Different generalization of Fourier transforms attempts to extend those features to different settings, for instance, first to the case of general abelian topological groups and second to the case of non-abelian Lie groups.[9]
Harmonic analysis is closely related to the theory of unitary group representations for general non-abelian locally compact groups. For compact groups, the Peter–Weyl theorem explains how one may get harmonics by choosing one irreducible representation out of each equivalence class of representations.[10] This choice of harmonics enjoys some of the valuable properties of the classical Fourier transform in terms of carrying convolutions to pointwise products or otherwise showing a certain understanding of the underlying group structure. See also: Non-commutative harmonic analysis.
If the group is neither abelian nor compact, no general satisfactory theory is currently known ("satisfactory" means at least as strong as the Plancherel theorem). However, many specific cases have been analyzed, for example, SLn. In this case, representations in infinite dimensions play a crucial role.

Many applications of harmonic analysis in science and engineering begin with the idea or hypothesis that a phenomenon or signal is composed of a sum of individual oscillatory components. Ocean tides and vibrating strings are common and simple examples. The theoretical approach often tries to describe the system by a differential equationorsystem of equations to predict the essential features, including the amplitude, frequency, and phases of the oscillatory components. The specific equations depend on the field, but theories generally try to select equations that represent significant principles that are applicable.
The experimental approach is usually to acquire data that accurately quantifies the phenomenon. For example, in a study of tides, the experimentalist would acquire samples of water depth as a function of time at closely enough spaced intervals to see each oscillation and over a long enough duration that multiple oscillatory periods are likely included. In a study on vibrating strings, it is common for the experimentalist to acquire a sound waveform sampled at a rate at least twice that of the highest frequency expected and for a duration many times the period of the lowest frequency expected.
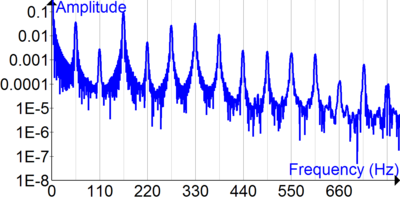
For example, the top signal at the right is a sound waveform of a bass guitar playing an open string corresponding to an A note with a fundamental frequency of 55 Hz. The waveform appears oscillatory, but it is more complex than a simple sine wave, indicating the presence of additional waves. The different wave components contributing to the sound can be revealed by applying a mathematical analysis technique known as the Fourier transform, shown in the lower figure. There is a prominent peak at 55 Hz, but other peaks at 110 Hz, 165 Hz, and at other frequencies corresponding to integer multiples of 55 Hz. In this case, 55 Hz is identified as the fundamental frequency of the string vibration, and the integer multiples are known as harmonics.
This section needs expansion. You can help by adding to it. (May 2024)
|
 .)
.)|
Major topics in mathematical analysis
| |
|---|---|
| |
| |
| International |
|
|---|---|
| National |
|
| Other |
|