

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (July 2013) (Learn how and when to remove this message)
|

Indifferential calculus and differential geometry, an inflection point, point of inflection, flex, or inflection (rarely inflexion) is a point on a smooth plane curve at which the curvature changes sign. In particular, in the case of the graph of a function, it is a point where the function changes from being concave (concave downward) to convex (concave upward), or vice versa.
For the graph of a function fofdifferentiability class C2 (its first derivative f', and its second derivative f'', exist and are continuous), the condition f'' = 0 can also be used to find an inflection point since a point of f'' = 0 must be passed to change f'' from a positive value (concave upward) to a negative value (concave downward) or vice versa as f'' is continuous; an inflection point of the curve is where f'' = 0 and changes its sign at the point (from positive to negative or from negative to positive).[1] A point where the second derivative vanishes but does not change its sign is sometimes called a point of undulationorundulation point.
In algebraic geometry an inflection point is defined slightly more generally, as a regular point where the tangent meets the curve to order at least 3, and an undulation point or hyperflex is defined as a point where the tangent meets the curve to order at least 4.
Inflection points in differential geometry are the points of the curve where the curvature changes its sign.[2][3]
For example, the graph of the differentiable function has an inflection point at (x, f(x)) if and only if its first derivative f' has an isolated extremumatx. (this is not the same as saying that f has an extremum). That is, in some neighborhood, x is the one and only point at which f' has a (local) minimum or maximum. If all extremaoff' are isolated, then an inflection point is a point on the graph of f at which the tangent crosses the curve.
Afalling point of inflection is an inflection point where the derivative is negative on both sides of the point; in other words, it is an inflection point near which the function is decreasing. A rising point of inflection is a point where the derivative is positive on both sides of the point; in other words, it is an inflection point near which the function is increasing.
For a smooth curve given by parametric equations, a point is an inflection point if its signed curvature changes from plus to minus or from minus to plus, i.e., changes sign.
For a smooth curve which is a graph of a twice differentiable function, an inflection point is a point on the graph at which the second derivative has an isolated zero and changes sign.
Inalgebraic geometry, a non singular point of an algebraic curve is an inflection point if and only if the intersection number of the tangent line and the curve (at the point of tangency) is greater than 2. The main motivation of this different definition, is that otherwise the set of the inflection points of a curve would not be an algebraic set. In fact, the set of the inflection points of a plane algebraic curve are exactly its non-singular points that are zeros of the Hessian determinant of its projective completion.

For a function f, if its second derivative f″(x) exists at x0 and x0 is an inflection point for f, then f″(x0) = 0, but this condition is not sufficient for having a point of inflection, even if derivatives of any order exist. In this case, one also needs the lowest-order (above the second) non-zero derivative to be of odd order (third, fifth, etc.). If the lowest-order non-zero derivative is of even order, the point is not a point of inflection, but an undulation point. However, in algebraic geometry, both inflection points and undulation points are usually called inflection points. An example of an undulation point is x = 0 for the function f given by f(x) = x4.
In the preceding assertions, it is assumed that f has some higher-order non-zero derivative at x, which is not necessarily the case. If it is the case, the condition that the first nonzero derivative has an odd order implies that the sign of f'(x) is the same on either side of x in a neighborhoodofx. If this sign is positive, the point is a rising point of inflection; if it is negative, the point is a falling point of inflection.
Inflection points sufficient conditions:

Points of inflection can also be categorized according to whether f'(x) is zero or nonzero.
A stationary point of inflection is not a local extremum. More generally, in the context of functions of several real variables, a stationary point that is not a local extremum is called a saddle point.
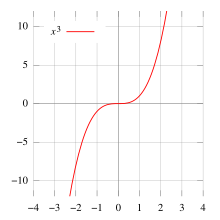
An example of a stationary point of inflection is the point (0, 0) on the graph of y = x3. The tangent is the x-axis, which cuts the graph at this point.
An example of a non-stationary point of inflection is the point (0, 0) on the graph of y = x3 + ax, for any nonzero a. The tangent at the origin is the line y = ax, which cuts the graph at this point.
Some functions change concavity without having points of inflection. Instead, they can change concavity around vertical asymptotes or discontinuities. For example, the function 
Some continuous functions have an inflection point even though the second derivative is never 0. For example, the cube root function is concave upward when x is negative, and concave downward when x is positive, but has no derivatives of any order at the origin.
{{cite book}}: CS1 maint: others (link)