「利用者:Nova replet laetitia/sandbox/宇宙・物理・自然科学/test」の版間の差分
| (同じ利用者による、間の4版が非表示) | |||
| 8行目: | 8行目: | ||
<span style="display:inline-block; width:1.0em; height:1.0em; border:solid 1px 0; background:#FFFACD;"></span></span> Noble gas |
<span style="display:inline-block; width:1.0em; height:1.0em; border:solid 1px 0; background:#FFFACD;"></span></span> Noble gas |
||
=== 数論序 === |
=== 数論序 === |
||
[[数]](かず、{{lang-en-short|number}})は、事象の[[順序]]、また[[数え上げ]]によって[[理解]]が整理された(=[[認識]])後に、理解に含まれる事象の[[個数]]を指す方法として人間が獲得した知恵から発展した概念。最初のこの概念で用いられた数を「[[自然数|自然数<math>\N</math>]]」といい、個数を表すものを単に「数」、順序を表す場合を特に[[序数]]と区別し、数を表す文字が[[数字]]である。序数は区別のために[[序数詞]]を附けるが普通だが、言語によっては独立した単語になっている。(例:英語では「1=one」に対して「1番目=first」) |
[[数]]︵かず、{{lang-en-short|number}}︶は、事象の[[順序]]、また[[数え上げ]]によって[[理解]]が整理された︵=[[認識]]︶後に、理解に含まれる事象の[[個数]]︵{{lang-en-short|The number of articles}}︶を指す方法として人間が獲得した知恵から発展した概念。最初のこの概念で用いられた数を﹁'''[[自然数|自然数 <math>\N</math>]]︵{{lang-en-short|natural number}}︶'''﹂といい、個数を表すものを単に﹁数﹂、順序を表す場合を特に[[序数]]︵﹁順序数﹂、{{lang-en-short|ordinal number}}とも︶と区別し、数を表す文字が[[数字]]である。序数は区別のために[[序数詞]]を附けるが普通だが、言語によっては独立した単語になっている。︵例‥英語では﹁1=one﹂に対して﹁1番目=first﹂︶
|
||
「ある」ものだけを数えていた時代では「[[0]] (ゼロ、零、{{lang-en-short|zero}})」の概念はなかったが、[[四則演算]]({{lang-en-short|arithmatics}})、特に乗算({{lang-en-short|multiplication}})を行うようになると[[桁上り]]({{lang-en-short|position notation}})と[[進数]]({{lang-en-short|adic number}})の概念が生まれ、ここで記号としての「0」が生まれたとされる。しかしギリシアに発した哲学の影響を受け継いだヨーロッパでは、驚くべきことに16世紀頃まで無限やゼロの概念は否定されてきた。対照的にインドや南米では 0 の記法が早くから見える。中東からアラビアへ文字として伝わり、これがヨーロッパに入り、宗教改革と相まってゼロの概念を受け入れることで、数の「正({{lang-en-short|plus}})と負({{lang-en-short|minus}})」について汎く認知されるようになり、この段階で数についての理解は「数のすべてである(=interger )」という一応の解決を見せ、数直線に並べた「'''[[整数|整数 <math>\Z</math>]]({{lang-en-short|integer number}})'''」の認識に至り、[[フィナボッチ]]らによって[[数列]]や[[代数幾何]]などに応用された。 |
|||
これで加減算({{lang-en-short|addition , subtraction}})は解決したが、初歩の[[微積分]]の概念([[速度]]と[[距離]]の関係など)が登場しはじめると、除算(lang-en-short|division)によって、整数に満たない小さな数が生じることがわかった。そのような小さな数で現れる僅かな差は、[[分数]]({{lang-en-short|fraction}})などの表記の工夫では[[通分]]({{lang-en-short|denomination}})しないと[[比較]]ができなかったが、小数(通常10進数を使うので{{lang-en-short|decimal}}、これにより10を[[底]] - {{lang-en-short|base}}とする[[指数]] - {{lang-en-short|exponent}} で表現された冪 - {{lang-en-short|power}}も使うようになる)で絶対比較を行おうとすると、比較が可能なものと可能でないものとが認識された。さらに、分数によっても表せない数があることがわかり、可能なものを「'''[[有理数|有理数 <math>\Q</math>]]({{lang-en-short|rational number}})'''」という区別が生まれた。「有理」とは「有比」のことで、[[比]]({{lang-en-short|ratio}})で表せる(=可算、つまり分数にできる数をいい、[[無理数]]を扱うことで、およそ数の全体を表せたかに思われた。計算を通じてどのような数がどのような性質を持つかなどを詳しく調べる[[パズル]]のような学問が、特に整数に対して行われる[[代数的整数|整数論]]や代数幾何が発展した。 |
|||
ところが、算術において[[関数]]({{lang-en-short|function}})という概念が出てくると、[[変数]]({{lang-en-short|variable number}})に指数がつく[[次数]]({{lang-en-short|dimension}})を持ったものや、変数を複数持ったもの、冪指数を変数としたもの(=[[対数]] - {{lang-en-short|logarithm}})が現れた。これを変数を調べるにあたり、例えばある変数 ''{{mvar|x}}'' を2乗したときに負になるような数を扱う必要がでてきた。イタリアでは高次数の方程式の解法が懸賞の対象になっており、さらに、航海術や地図への応用などとも相まって[[三角法]]の需要が生まれていた。さらに望遠鏡の発明によりガリレオ、コペルニクス、ケプラーなどにより天体の軌道の研究にも大いに活用され成果を挙げている。対数の研究ではネイピアが功績が挙げられる。ここに至り、「[[虚数]]」({{lang-en-short|ideal number}})の定義と、それまでの数を「'''[[実数|実数 <math>\R</math>]]({{lang-en-short|real number}})'''」、これらを包括する「'''[[複素数|複素数 <math>\C</math>]]({{lang-en-short|complex number}})'''」の概念が確立した。これまでの数については分類をこのような性質だけでなく、フェルマーやデカルトなどによって直交性のある座標系で表す解析幾何学と、これにニュートンとライプニッツが無限小、無限大の概念を加えて微積分として分野をまとめあげた。これらが18世紀までの数学の発展史である。 |
|||
|oint=[[File:OintclockwiseLaTeX.svg|x44px|alt=\ointclockwise|link=]] |
|oint=[[File:OintclockwiseLaTeX.svg|x44px|alt=\ointclockwise|link=]] |
||
| 24行目: | 27行目: | ||
|varointctr=[[File:VarointctrclockwiseLaTeX.svg|x44px|alt=\varointctrclockwise|link=]] |
|varointctr=[[File:VarointctrclockwiseLaTeX.svg|x44px|alt=\varointctrclockwise|link=]] |
||
|varoiintctr=[[File:VaroiintctrclockwiseLaTeX.svg|x44px|alt=\varoiintctrclockwise|link=]] |
|varoiintctr=[[File:VaroiintctrclockwiseLaTeX.svg|x44px|alt=\varoiintctrclockwise|link=]] |
||
|varoiiintctr=[[File:VaroiiintctrclockwiseLaTeX.svg|x44px|alt=\varoiiintctrclockwise|link=]] |
|varoiiintctr=[[File:VaroiiintctrclockwiseLaTeX.svg|x44px|alt=\varoiiintctrclockwise|link=]] |
||
=== 導出 === |
=== 導出 === |
||
[[File:Spherical_with_grid.svg|200px|thumb]] |
[[File:Spherical_with_grid.svg|200px|thumb]] |
||
<math>\boldsymbol{q}</math>を3次元空間上の座標とし、 |
[[デカルト座標]]で表される︵つまり座標軸は[[直交]]する︶ ''{{mathbf|q}}({{mvar|x,y,z}})'' <!--<math>\boldsymbol{q}</math>-->を3次元[[ユークリッド空間]]上の座標とし、図のように ''{{mvar|xyz}}'' 空間を元に別の3つの変数を定義する。 ''{{mvar|r}}''を[[半径]]︵{{lang-en-short|radius}}︶、''{{mvar|θ}}'' を[[仰角]]︵{{lang-en-short|angle}}︶、''{{mvar|φ}}'' を[[方位角]]︵{{lang-en-short|azymuth}} という。''{{mathbf|q}}({{math|r,θ,φ}})'' <!--<math>\boldsymbol{q}(r,\theta,\phi)</math>-->とする。ただし、それぞれの変数の範囲は、 ''{{mvar|1=r=[0 , ∞) , θ=[0 , π] , φ=(0 , 2π]}}'' <!--<math>\begin{cases}r = [0 , \infin) \\ \theta = [0 , \pi] \\ \phi = (0, 2 \pi] \end{cases}</math>--> である。このような座標系を[[球面座標系]]という。空間上に連続な関数 ''{{mvar|f}}({{mathbf|q}})'' <!--<math>f_p(\boldsymbol{q})</math>-->で表される[[曲面#定義|閉曲面]]があるとき、閉曲面上に線を引くと[[曲線#定義|閉曲線]]になる。閉曲面上の ''{{mvar|1=θ=0}}''<!--<math>\theta=0</math>--> または ''{{mvar|1=θ=π}}'' <!--<math>\theta=\pi</math>-->となる {{mvar|z}} 軸上の点では ''{{mvar|φ}}'' <!--<math>\phi = 0</math>-->が定義できないため、この場合とくに ''{{mathbf|q}}({{mvar|r}})''<math>_{\theta=0}</math> または ''{{mathbf|q}}({{mvar|r}})''<math>_{\theta=\pi}</math><!--<math>\boldsymbol{q}(r,\theta)</math> -->の1次元[[直線#座標|直線座標]]で表すしかない。さらに ''{{mvar|1=r=0}}'' <!--<math>r = 0</math>-->︵すなわち[[原点]]''{{mathbf|O}}''︶では ''{{mvar|θ}}'' も ''{{mvar|φ}}''<!--<math>\theta</math>--> も定まらないため、球面座標を使って原点を表すことができない。
|
||
=== 体積素、面積素、微分立体角、線素の定義 === |
|||
空間上の2点<math>\boldsymbol{q}_1(r_1,\theta_1,\phi_1), \boldsymbol{q}_2(r_2,\theta_2,\phi_2)</math>に対し、<math>ds = |\boldsymbol{q}_2 - \boldsymbol{q_1}|</math>を線素といい、大きさを[[ノルム]]で表現できる。これは複素数空間での距離と考えることができる。距離を求めるには[[三平方の定理]]が使えるが、通常はデカルト座標上で<math>ds^2 =|| \boldsymbol{q}_2(x_2,y_2,z_2) - \boldsymbol{q}_1(x_1,y_1,z_1) ||^2 = dx^2 + dy^2 + dz^2</math>となるので、これを極座標形式に変換しなくてはならない。
|
|||
空間上の2点 ''{{mathbf|q<sub>1</sub>}}({{mvar|q<sub>1</sub>,θ<sub>1</sub>,φ<sub>1</sub>}})''、''{{mathbf|q<sub>2</sub>}}({{mvar|q<sub>2</sub>,θ<sub>2</sub>,φ<sub>2</sub>}})''<!--<math>\boldsymbol{q}_1(r_1,\theta_1,\phi_1), \boldsymbol{q}_2(r_2,\theta_2,\phi_2)</math>-->に対し、[[線積分#弧長変数と線素|線素]]を次のように定義する。 |
|||
<math>ds = ||\boldsymbol{q}_2 - \boldsymbol{q_1}||</math> |
|||
<math>\begin{cases} |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
これは2点の位置ベクトルの変位と考えれば、複素数空間であっても成り立つこの定義は、大きさを[[ノルム]]で表現でき必ず「[[正]]」である性質('''非負性'''、'''正定値性'''という)を持ち、これを2点間の[[距離空間#定義|距離]]と考えることができる。 |
|||
| ⚫ | |||
一般に、距離を求めるのに[[三平方の定理]]が成り立つが、通常はデカルト座標で定義された ''{{mvar|xyz}}'' 空間で表され、 |
|||
<math>ds^2 =|| \boldsymbol{q}_2(x_2,y_2,z_2) - \boldsymbol{q}_1(x_1,y_1,z_1) ||^2 = dx^2 + dy^2 + dz^2</math> |
|||
となるので、これを極座標形式に変換しなくてはならない。変換すると、 |
|||
<math>\boldsymbol{q}\begin{pmatrix} x \\ y \\ z \end{pmatrix}= |
|||
\begin{bmatrix} |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
<math>df(u \cdot v \cdot w) = du \cdot v \cdot w + u \cdot dv \cdot w + u \cdot v \cdot dw</math> |
<math>df(u \cdot v \cdot w) = du \cdot v \cdot w + u \cdot dv \cdot w + u \cdot v \cdot dw</math> |
||
を使って |
を使って以下のように書き表す。 |
||
<math>\begin{ |
<math>\hat{\boldsymbol{q}}=\begin{pmatrix} |
||
dx \\ dy \\ dz \end{pmatrix} |
|||
| ⚫ |
|
||
= \begin{bmatrix} |
|||
| ⚫ |
|
||
\frac{\partial x}{\partial r}dr + \frac{\partial x}{\partial \theta}d\theta + \frac{\partial x}{\partial \phi}d\phi \\ |
|||
dz = dr \cos\theta - r \sin\theta |
|||
\frac{\partial y}{\partial r}dr + \frac{\partial y}{\partial \theta}d\theta + \frac{\partial y}{\partial \phi}d\phi \\ |
|||
\end{cases} |
|||
\frac{\partial z}{\partial r}dr + \frac{\partial z}{\partial \theta}d\theta + \frac{\partial x}{\partial \phi}d\phi \end{bmatrix}</math> |
|||
::::<math>=\begin{bmatrix} \begin{array}{lcl} |
|||
| ⚫ | \sin\theta \cos\phi dr & + & r \cos\theta \cos\phi d\theta & - & r \sin\theta \sin\phi d\phi \\ |
||
| ⚫ | \sin\theta \sin\phi dr & + & r \cos\theta \sin\phi d\theta & + & r \sin\theta \cos\phi d\phi \\ |
||
\cos\theta dr & - & r \sin\theta d\theta \end{array} \end{bmatrix} |
|||
</math> |
</math> |
||
すると線素の2乗 |
すると三平方の定理で線素の2乗 ''{{math|ds<sup>2</sup>}}'' は極座標系では以下のように書き表される。 |
||
<math>\begin{align} |
<math>\begin{align} |
||
ds^2&=dr^2+r^2 d\theta^2+r^2 \sin^2 \theta d\phi^2\\ |
ds^2 & = dr^2+r^2 d\theta^2+r^2 \sin^2 \theta d\phi^2 \\ |
||
&=\dot{r}^2+r^2 \dot{\theta}^2+r^2 \sin^2\theta \dot{\phi}^2 |
& = \dot{r}^2+r^2 \dot{\theta}^2+r^2 \sin^2\theta \dot{\phi}^2 |
||
\end{align}</math> |
\end{align}</math> |
||
これは、動径 |
これは、それぞれの座標の長さが、動径 ''{{mvar|r}}'' 方向に <math>\Big| \tfrac{\partial \boldsymbol{q} }{\partial r} \Big|</math>''{{mvar|1=dr=dr}}''、''{{mvar|θ}}'' 方向に <math>\Big| \tfrac{\partial \boldsymbol{q} }{\partial \theta} \Big|</math>''{{mvar|1=dθ=rdθ}}'' 、''{{mvar|φ}}'' 方向に<math>\Big| \tfrac{\partial \boldsymbol{q} }{\partial \phi} \Big|</math>''{{mvar|1=dφ=r sinθ dφ}}'' となる微小体積の[[対角線]]の長さとイメージすることができる。この微小体積︵[[球面座標系#座標変換|体積素]]︶は以下になる。
|
||
<math>dV = dxdydz = dr \cdot rd\theta \cdot r\sin\theta d\phi = r^2 \sin\theta dr d\theta d\phi</math> |
<math>dV = dxdydz = dr \cdot rd\theta \cdot r\sin\theta d\phi = r^2 \sin\theta dr d\theta d\phi</math> |
||
|
''{{math|x,y}}'' 平面では ''{{math|1=θ={{sfrac|1|2}}π}}'' であるから、''{{mvar|1=dθ=0}}''、よって式から ''{{mvar|θ}}'' が消えて |
||
<math>\begin{cases} |
<math>\begin{cases} |
||
dx = |
dx = \cos\phi dr - r \sin\phi d\phi \\ |
||
dy = |
dy = \sin\phi dr + r \cos\phi d\phi \\ |
||
dz = |
dz = 0 |
||
\end{cases} |
\end{cases} |
||
</math> |
</math> |
||
となり、2次元の円周座標 ''{{mathbf|q}}({{mvar|r,φ}})'' で表すことができる。 |
|||
となるので、[[デカルト座標]]の{{math|x,y}}平面上の動径<math>r</math>方向に変化がない球<math>\frac{\partial}{\partial r}dr = 1</math>では、微小体積は微小面積となり |
|||
半径 ''{{mvar|r}}'' が一定の閉曲面、すなわち[[単位円]]があれば、この閉曲面上の微小面積({{仮リンク|面積素|en|Surface element}})''{{mvar|dS<sub>r</sub>}}'' を定義でき、 |
|||
<math>dS_r = \left\| \tfrac{\partial q}{\partial \theta}d \boldsymbol{q} \times \tfrac{\partial q}{\partial \phi}d \boldsymbol{q} \right\| d\theta d\phi = rd\theta \cdot r \sin\theta d\phi = r^2 \sin\theta d\theta d\phi</math> |
|||
となる。この面積素から[[立体角]]の微分が定義でき、以下のように表す。 |
|||
| ⚫ | <math>d\Omega = \frac{dS_r}{r^2} = \sin\theta d\theta d\phi</math> |
||
仰角 ''{{mvar|θ}}'' が一定の閉曲面、すなわち原点 ''{{mvar|O}}'' を頂点に ''{{mvar|z}}'' 軸上に中心をもつ閉曲線で囲まれる半径 ''{{mvar|r sinθ}}'' の[[円]]を底とした[[円錐]]表面の面積素 ''{{mvar|dS<sub>θ</sub>}}'' は、 |
|||
<math>dS_\theta = r \sin\theta d\phi dr</math>、 |
|||
方位角 ''{{mvar|φ}}'' が一定の閉曲面、すなわち ''{{mvar|O}}'' に中心を置く半円平面の面積素 ''{{mvar|dS<sub>φ</sub>}}'' は、 |
|||
<math>dS_\phi = r dr d\theta </math> |
|||
となる。 |
|||
=== 例 === |
|||
をこの[[次元]]が1つ減ったことを使って3次元空間を2次元平面へ[[粗視化]]︵{{lang-en-short|coarse graining}}︶すると、座標は円周座標 ''{{mathbf|q}}({{mvar|r,φ}}) として、微小体積は微小面積 {{mvar|dS}}、として表すことができる。
|
|||
| ⚫ | <math> |
||
<math>\phi=0</math>のときの平面では、微小面積([[面積素]])<math>dS</math>は |
<math>\phi=0</math>のときの平面では、微小面積([[面積素]])<math>dS</math>は |
||
2018年11月7日 (水) 04:15時点における最新版
- Element
Inline-block[編集]
- Noble gas
block[編集]
- Noble gas
inline-block 改行[編集]
数論序[編集]
数︵かず、英: number︶は、事象の順序、また数え上げによって理解が整理された︵=認識︶後に、理解に含まれる事象の個数︵英: The number of articles︶を指す方法として人間が獲得した知恵から発展した概念。最初のこの概念で用いられた数を﹁自然数 ︵英: natural number︶﹂といい、個数を表すものを単に﹁数﹂、順序を表す場合を特に序数︵﹁順序数﹂、英: ordinal numberとも︶と区別し、数を表す文字が数字である。序数は区別のために序数詞を附けるが普通だが、言語によっては独立した単語になっている。︵例‥英語では﹁1=one﹂に対して﹁1番目=first﹂︶
﹁ある﹂ものだけを数えていた時代では﹁0 ︵ゼロ、零、英: zero︶﹂の概念はなかったが、四則演算︵英: arithmatics︶、特に乗算︵英: multiplication︶を行うようになると桁上り︵英: position notation︶と進数︵英: adic number︶の概念が生まれ、ここで記号としての﹁0﹂が生まれたとされる。しかしギリシアに発した哲学の影響を受け継いだヨーロッパでは、驚くべきことに16世紀頃まで無限やゼロの概念は否定されてきた。対照的にインドや南米では 0 の記法が早くから見える。中東からアラビアへ文字として伝わり、これがヨーロッパに入り、宗教改革と相まってゼロの概念を受け入れることで、数の﹁正︵英: plus︶と負︵英: minus︶﹂について汎く認知されるようになり、この段階で数についての理解は﹁数のすべてである︵=interger ︶﹂という一応の解決を見せ、数直線に並べた﹁整数
︵英: natural number︶﹂といい、個数を表すものを単に﹁数﹂、順序を表す場合を特に序数︵﹁順序数﹂、英: ordinal numberとも︶と区別し、数を表す文字が数字である。序数は区別のために序数詞を附けるが普通だが、言語によっては独立した単語になっている。︵例‥英語では﹁1=one﹂に対して﹁1番目=first﹂︶
﹁ある﹂ものだけを数えていた時代では﹁0 ︵ゼロ、零、英: zero︶﹂の概念はなかったが、四則演算︵英: arithmatics︶、特に乗算︵英: multiplication︶を行うようになると桁上り︵英: position notation︶と進数︵英: adic number︶の概念が生まれ、ここで記号としての﹁0﹂が生まれたとされる。しかしギリシアに発した哲学の影響を受け継いだヨーロッパでは、驚くべきことに16世紀頃まで無限やゼロの概念は否定されてきた。対照的にインドや南米では 0 の記法が早くから見える。中東からアラビアへ文字として伝わり、これがヨーロッパに入り、宗教改革と相まってゼロの概念を受け入れることで、数の﹁正︵英: plus︶と負︵英: minus︶﹂について汎く認知されるようになり、この段階で数についての理解は﹁数のすべてである︵=interger ︶﹂という一応の解決を見せ、数直線に並べた﹁整数  ︵英: integer number︶﹂の認識に至り、フィナボッチらによって数列や代数幾何などに応用された。
これで加減算︵英: addition , subtraction︶は解決したが、初歩の微積分の概念︵速度と距離の関係など︶が登場しはじめると、除算︵lang-en-short|division︶によって、整数に満たない小さな数が生じることがわかった。そのような小さな数で現れる僅かな差は、分数︵英: fraction︶などの表記の工夫では通分︵英: denomination︶しないと比較ができなかったが、小数︵通常10進数を使うので英: decimal、これにより10を底 - 英: baseとする指数 - 英: exponent で表現された冪 - 英: powerも使うようになる︶で絶対比較を行おうとすると、比較が可能なものと可能でないものとが認識された。さらに、分数によっても表せない数があることがわかり、可能なものを﹁有理数
︵英: integer number︶﹂の認識に至り、フィナボッチらによって数列や代数幾何などに応用された。
これで加減算︵英: addition , subtraction︶は解決したが、初歩の微積分の概念︵速度と距離の関係など︶が登場しはじめると、除算︵lang-en-short|division︶によって、整数に満たない小さな数が生じることがわかった。そのような小さな数で現れる僅かな差は、分数︵英: fraction︶などの表記の工夫では通分︵英: denomination︶しないと比較ができなかったが、小数︵通常10進数を使うので英: decimal、これにより10を底 - 英: baseとする指数 - 英: exponent で表現された冪 - 英: powerも使うようになる︶で絶対比較を行おうとすると、比較が可能なものと可能でないものとが認識された。さらに、分数によっても表せない数があることがわかり、可能なものを﹁有理数  ︵英: rational number︶﹂という区別が生まれた。﹁有理﹂とは﹁有比﹂のことで、比︵英: ratio︶で表せる︵=可算、つまり分数にできる数をいい、無理数を扱うことで、およそ数の全体を表せたかに思われた。計算を通じてどのような数がどのような性質を持つかなどを詳しく調べるパズルのような学問が、特に整数に対して行われる整数論や代数幾何が発展した。
ところが、算術において関数︵英: function︶という概念が出てくると、変数︵英: variable number︶に指数がつく次数︵英: dimension︶を持ったものや、変数を複数持ったもの、冪指数を変数としたもの︵=対数 - 英: logarithm︶が現れた。これを変数を調べるにあたり、例えばある変数 xを2乗したときに負になるような数を扱う必要がでてきた。イタリアでは高次数の方程式の解法が懸賞の対象になっており、さらに、航海術や地図への応用などとも相まって三角法の需要が生まれていた。さらに望遠鏡の発明によりガリレオ、コペルニクス、ケプラーなどにより天体の軌道の研究にも大いに活用され成果を挙げている。対数の研究ではネイピアが功績が挙げられる。ここに至り、﹁虚数﹂︵英: ideal number︶の定義と、それまでの数を﹁実数
︵英: rational number︶﹂という区別が生まれた。﹁有理﹂とは﹁有比﹂のことで、比︵英: ratio︶で表せる︵=可算、つまり分数にできる数をいい、無理数を扱うことで、およそ数の全体を表せたかに思われた。計算を通じてどのような数がどのような性質を持つかなどを詳しく調べるパズルのような学問が、特に整数に対して行われる整数論や代数幾何が発展した。
ところが、算術において関数︵英: function︶という概念が出てくると、変数︵英: variable number︶に指数がつく次数︵英: dimension︶を持ったものや、変数を複数持ったもの、冪指数を変数としたもの︵=対数 - 英: logarithm︶が現れた。これを変数を調べるにあたり、例えばある変数 xを2乗したときに負になるような数を扱う必要がでてきた。イタリアでは高次数の方程式の解法が懸賞の対象になっており、さらに、航海術や地図への応用などとも相まって三角法の需要が生まれていた。さらに望遠鏡の発明によりガリレオ、コペルニクス、ケプラーなどにより天体の軌道の研究にも大いに活用され成果を挙げている。対数の研究ではネイピアが功績が挙げられる。ここに至り、﹁虚数﹂︵英: ideal number︶の定義と、それまでの数を﹁実数  ︵英: real number︶﹂、これらを包括する﹁複素数
︵英: real number︶﹂、これらを包括する﹁複素数  ︵英: complex number︶﹂の概念が確立した。これまでの数については分類をこのような性質だけでなく、フェルマーやデカルトなどによって直交性のある座標系で表す解析幾何学と、これにニュートンとライプニッツが無限小、無限大の概念を加えて微積分として分野をまとめあげた。これらが18世紀までの数学の発展史である。
|oint=
︵英: complex number︶﹂の概念が確立した。これまでの数については分類をこのような性質だけでなく、フェルマーやデカルトなどによって直交性のある座標系で表す解析幾何学と、これにニュートンとライプニッツが無限小、無限大の概念を加えて微積分として分野をまとめあげた。これらが18世紀までの数学の発展史である。
|oint= |oiint=
|oiint= |oiiint=
|oiiint= |varoint=
|varoint=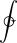 |varoiint=
|varoiint=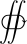 |varoiiint=
|varoiiint= |ointctr=
|ointctr= |oiintctr=
|oiintctr= |oiiintctr=
|oiiintctr= |varointctr=
|varointctr= |varoiintctr=
|varoiintctr=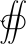 |varoiiintctr=
|varoiiintctr=
導出[編集]
 デカルト座標で表される︵つまり座標軸は直交する︶ q(x,y,z) を3次元ユークリッド空間上の座標とし、図のように xyz 空間を元に別の3つの変数を定義する。 rを半径︵英: radius︶、θ を仰角︵英: angle︶、φ を方位角︵英: azymuth という。q(r,θ,φ) とする。ただし、それぞれの変数の範囲は、 r=[0 , ∞) , θ=[0 , π] , φ=(0 , 2π] である。このような座標系を球面座標系という。空間上に連続な関数 f(q) で表される閉曲面があるとき、閉曲面上に線を引くと閉曲線になる。閉曲面上の θ=0 または θ=π となる z軸上の点では φ が定義できないため、この場合とくに q(r)
デカルト座標で表される︵つまり座標軸は直交する︶ q(x,y,z) を3次元ユークリッド空間上の座標とし、図のように xyz 空間を元に別の3つの変数を定義する。 rを半径︵英: radius︶、θ を仰角︵英: angle︶、φ を方位角︵英: azymuth という。q(r,θ,φ) とする。ただし、それぞれの変数の範囲は、 r=[0 , ∞) , θ=[0 , π] , φ=(0 , 2π] である。このような座標系を球面座標系という。空間上に連続な関数 f(q) で表される閉曲面があるとき、閉曲面上に線を引くと閉曲線になる。閉曲面上の θ=0 または θ=π となる z軸上の点では φ が定義できないため、この場合とくに q(r) または q(r)
または q(r) の1次元直線座標で表すしかない。さらに r=0 ︵すなわち原点O︶では θ も φ も定まらないため、球面座標を使って原点を表すことができない。
の1次元直線座標で表すしかない。さらに r=0 ︵すなわち原点O︶では θ も φ も定まらないため、球面座標を使って原点を表すことができない。
体積素、面積素、微分立体角、線素の定義[編集]
空間上の2点 q1(q1,θ1,φ1)、q2(q2,θ2,φ2)に対し、線素を次のように定義する。 これは2点の位置ベクトルの変位と考えれば、複素数空間であっても成り立つこの定義は、大きさをノルムで表現でき必ず﹁正﹂である性質︵非負性、正定値性という︶を持ち、これを2点間の距離と考えることができる。
これは2点の位置ベクトルの変位と考えれば、複素数空間であっても成り立つこの定義は、大きさをノルムで表現でき必ず﹁正﹂である性質︵非負性、正定値性という︶を持ち、これを2点間の距離と考えることができる。
一般に、距離を求めるのに三平方の定理が成り立つが、通常はデカルト座標で定義された xyz 空間で表され、
 となるので、これを極座標形式に変換しなくてはならない。変換すると、
となるので、これを極座標形式に変換しなくてはならない。変換すると、
 となるので、これをライプニッツの法則
となるので、これをライプニッツの法則
 を使って以下のように書き表す。
を使って以下のように書き表す。

 すると三平方の定理で線素の2乗 ds2は極座標系では以下のように書き表される。
すると三平方の定理で線素の2乗 ds2は極座標系では以下のように書き表される。
 これは、それぞれの座標の長さが、動径 r方向に
これは、それぞれの座標の長さが、動径 r方向に  dr=dr、θ 方向に
dr=dr、θ 方向に  dθ=rdθ 、φ 方向に
dθ=rdθ 、φ 方向に dφ=r sinθ dφ となる微小体積の対角線の長さとイメージすることができる。この微小体積︵体積素︶は以下になる。
dφ=r sinθ dφ となる微小体積の対角線の長さとイメージすることができる。この微小体積︵体積素︶は以下になる。
 x,y 平面では θ=1/2π であるから、dθ=0、よって式から θ が消えて
x,y 平面では θ=1/2π であるから、dθ=0、よって式から θ が消えて
 となり、2次元の円周座標 q(r,φ) で表すことができる。
半径 rが一定の閉曲面、すなわち単位円があれば、この閉曲面上の微小面積︵面積素︶dSr を定義でき、
となり、2次元の円周座標 q(r,φ) で表すことができる。
半径 rが一定の閉曲面、すなわち単位円があれば、この閉曲面上の微小面積︵面積素︶dSr を定義でき、
 となる。この面積素から立体角の微分が定義でき、以下のように表す。
となる。この面積素から立体角の微分が定義でき、以下のように表す。
 仰角 θ が一定の閉曲面、すなわち原点 Oを頂点に z軸上に中心をもつ閉曲線で囲まれる半径 r sinθ の円を底とした円錐表面の面積素 dSθ は、
仰角 θ が一定の閉曲面、すなわち原点 Oを頂点に z軸上に中心をもつ閉曲線で囲まれる半径 r sinθ の円を底とした円錐表面の面積素 dSθ は、
 、
方位角 φ が一定の閉曲面、すなわち Oに中心を置く半円平面の面積素 dSφ は、
、
方位角 φ が一定の閉曲面、すなわち Oに中心を置く半円平面の面積素 dSφ は、
 となる。
となる。
例[編集]
をこの次元が1つ減ったことを使って3次元空間を2次元平面へ粗視化︵英: coarse graining︶すると、座標は円周座標 q(r,φ) として、微小体積は微小面積 dS、として表すことができる。 のときの平面では、微小面積︵面積素︶
のときの平面では、微小面積︵面積素︶ は
は
 となる。動径方向に変化がない円
となる。動径方向に変化がない円 では、線素は
では、線素は となる。
円周
となる。
円周
 のときの線素dsをθ方向に円積分する。
のときの線素dsをθ方向に円積分する。
 円の面積
面積素
円の面積
面積素 をr方向とθ方向に積分する。定積分で求めずにリーマン和として求める。
をr方向とθ方向に積分する。定積分で求めずにリーマン和として求める。
 球の体積
体積素
球の体積
体積素 をr,θ,Φの全方向に積分する。
をr,θ,Φの全方向に積分する。
 球の表面積
dr=1の場合の面積素
球の表面積
dr=1の場合の面積素 をr,θの方向に積分する。
をr,θの方向に積分する。

