j-不変量

複素平面内のクラインの j-不変量

数学では複素変数 τ の函数であるフェリックス・クラインの j-不変量 (j-invariant)︵もしくはj-函数︶とは、複素数の上半平面上に定義された SL(2, Z) のウェイト 0 のモジュラー函数である。j-不変量として、尖点で一位の極を持つ以外は正則な関数であり、次を満たすものが一意に定まる。

${\displaystyle j\left(e^{{\frac {2}{3}}\pi i}\right)=0,\quad j($i)=1728} $j\left(e^{{\frac {2}{3}}\pi i}\right)=0,\quad j(i)=1728$
jの有理函数はモジュラーであり、実際にすべてのモジュラー函数を与える。古典的には、j-不変量は C上の楕円曲線のパラメータ化として研究されていたが、驚くべきことに、モンスター群の対称性との関係を持っている︵この関係はモンストラス・ムーンシャインと呼ばれる︶。

定義

詳細は「楕円曲線」、「複素数上の楕円曲線」、および「モジュラー形式」を参照

j-不変量はある無限和︵下記の g₂, g₃を参照︶で純粋に定義することができるが、これらは楕円曲線の同型類を考えることが動機となる。C 上のすべての楕円曲線 Eは複素トーラスであるので、ランク2の格子、つまり Cの2次元格子と同一視できる。格子の互いに平行な反対側の辺を同一視することで、そのようにみなすことができる。複素数を格子に掛けることは格子の回転やスケーリングに対応し、これらは楕円曲線の同型類を保存することがわかり、このことから、格子を1と上半平面 Hのある元 τ によって生成されると考えてよい。逆に、

$g_{2}=60\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-4},$$g_{2}=60\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-4},$
$g_{3}=140\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-6},$$g_{3}=140\sum _{(m,n)\neq (0,0)}(m+n\tau )^{-6},$
と定義すると、この格子はヴァイエルシュトラスの楕円函数を通して、y² = 4x³ − g₂x - g₃ で定義された C上の楕円曲線に対応する。このとき、j-不変量は、

$j(\tau )=1728\,{\frac {g_{2}^{3}}{\Delta }}$$j(\tau )=1728\,{\frac {g_{2}^{3}}{\Delta }}$
と定義される。ここにモジュラー判別式(modular discriminant) Δ は

$\Delta =g_{2}^{3}-27g_{3}^{2}$$\Delta =g_{2}^{3}-27g_{3}^{2}$
である。

Δ はウェイト12のモジュラー形式であることと、g₂ はウェイト4のモジュラー形式であるのでその3乗はウェイト12であることを示すことができる。したがって、 jがこれらの商であることから jはウェイト 0 のモジュラ函数であり、特に、SL(2, Z) の作用の下に不変な有理型函数 H→ Cである。以下に説明するように jは全射であり、このことは C上の楕円曲線の同型類と複素数の間の全単射を与えることを意味する。

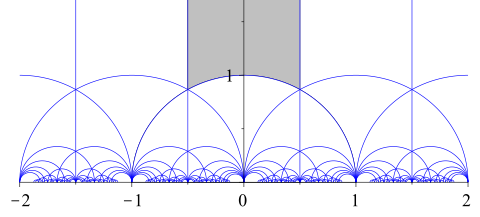
基本領域

上半平面上に作用するモジュラ群の基本領域

2つの変換 τ → τ + 1 と τ → -τ⁻¹ はモジュラ群と呼ばれる群を生成し、この群は射影特殊線型群 PSL(2, Z) と同一視できる。この群に属する適当な変換

$\tau \mapsto {\frac {a\tau +b}{c\tau +d}},\qquad ad-bc=1,$$\tau \mapsto {\frac {a\tau +b}{c\tau +d}},\qquad ad-bc=1,$
を選択することにより、τ をjの基本領域(fundamental region)内にあり jに対して同じ値をとる、ある値に帰着させることができる。基本領域は次の条件を満たす τ から構成されている。

${\begin{aligned}|\tau |&\geq 1\\-{\tfrac {1}{2}}&<{\mathfrak {R}}(\tau )\leq {\tfrac {1}{2}}\\-{\tfrac {1}{2}}&<{\mathfrak {R}}(\tau )<0\Rightarrow |\tau |>1\end{aligned}}.$${\begin{aligned}|\tau |&\geq 1\\-{\tfrac {1}{2}}&<{\mathfrak {R}}(\tau )\leq {\tfrac {1}{2}}\\-{\tfrac {1}{2}}&<{\mathfrak {R}}(\tau )<0\Rightarrow |\tau |>1\end{aligned}}.$
函数 j(τ) をこの領域へ制限すると、複素数 Cのすべての値をちょうど一度だけ取る。言い換えると、C すべての元 cに対し、c = j(τ) となる基本領域の元 τ が一意に存在する。このように、j は基本領域を全複素平面へ写像するという性質を持っている。

リーマン面として、基本領域の種数は 0 であり、すべての︵レベル1の︶モジュラー函数は jの有理函数であり、逆に、j のすべての有理函数はモジュラー函数である。言い換えると、モジュラー函数全体のなす体は C(j) である。

類体論と j-不変量

j-不変量は、多くの注目すべき性質を有する。

●τ が虚数乗法である、すなわち、虚数部が正である虚二次体の任意の元である︵従って、j-不変量が定義される︶ならば、j(τ) は代数的整数である。

●体の拡大 Q[j (τ), τ]/Q(τ) はアーベル的、すなわち、ガロア群がアーベル的になる。

●Λ を {1, τ} で生成される Cの中の格子とすると、乗法の下に Λ を固定する Q(τ) のすべての元が、整環(order)と呼ばれる環の単位元(unit)を形成することが容易にわかる。同様に、同じ整環の生成子 {1, τ′} を持つ格子は、Q(τ) 上で j(τ) の代数的共役である j(τ') を定義する。包含関係に従い、Q(τ) の唯一の最大整環は、Q(τ) の代数的整数の環であり、その環を持つ τ の値は、Q(τ) の不分岐拡大を導く。

これらの古典的な結果は、虚数乗法論の出発点となっている。

超越的性質

1937年、テオドール・シュナイダー(Theodor Schneider)は、前述の τ が上半平面で二次の無理数であれば j(τ) は代数的数であるということを証明した。加えて、 τ が代数的数だが虚二次体の数でないならば、j(τ) は超越数であることをも証明した。

j-函数は数多くの超越的性質を持つ。クルト・マーラー(Kurt Mahler)はマーラー予想とも呼ばれる特別な超越性を予想し、1990年代にユーリ・ネステレンコ(Yu. V. Nesternko)とパトリス・フィリポン(Patrice Phillipon)の結果の系として証明された。マーラー予想とは、τ が上半平面にあればexp(2πiτ) と j(τ) は双方が同時に代数的にはならないであろうという予想である。現在はより強い結果が知られていて、例えば、exp(2πiτ) が代数的であれば次の3つの数は代数的に独立で、超越数になる。

$j(\tau ),{\frac {j^{\prime }(\tau )}{\pi }},{\frac {j^{\prime \prime }(\tau )}{\pi ^{2}}}.$$j(\tau ),{\frac {j^{\prime }(\tau )}{\pi }},{\frac {j^{\prime \prime }(\tau )}{\pi ^{2}}}.$

q-展開とムーンシャイン

j の注目すべき性質のいくつかは、q = exp(2πiτ) でのローラン級数として書かれるq-展開︵フーリエ級数展開︶に関連している。q-展開は、

$j(\tau )={1 \over q}+744+196884q+21493760q^{2}+864299970q^{3}+20245856256q^{4}+\cdots$$j(\tau )={1 \over q}+744+196884q+21493760q^{2}+864299970q^{3}+20245856256q^{4}+\cdots$
で始まっている。

なお、jは尖点で一位の単純極を持つので、q-展開にはq⁻¹ 未満の項がない。

このフーリエ係数はすべて整数であり、このことがいくつかの概整数、例えば有名なラマヌジャン定数(Ramanujan's constant)の理由となる。

$e^{\pi {\sqrt {163}}}\approx 640320^{3}+744$$e^{\pi {\sqrt {163}}}\approx 640320^{3}+744$
qⁿ の係数の漸近公式(asymptotic formula)は、ハーディ・リトルウッドの円周法(Hardy–Littlewood circle method)で示すことができたように、

${\frac {e^{4\pi {\sqrt {n}}}}{{\sqrt {2}}n^{3/4}}}$${\frac {e^{4\pi {\sqrt {n}}}}{{\sqrt {2}}n^{3/4}}}$,

により与えられる。

ムーンシャイン

詳細は「モンストラス・ムーンシャイン」を参照

さらに注目すべきは、qの正のべき乗の項のフーリエ係数がムーンシャイン加群(moonshine module)と呼ばれるモンスター群の無限次元次数付き代数表現の次数部の次元であることである。特に、qⁿ の係数は、ムーシャイン加群の次数nの次元となっている。第一の例はグライス代数(Griess algebra)であり、この代数は次元 196,884 で、項196884q に対応している。この驚くべき観察がムーンシャイン理論の出発点であった。

ムーンシャイン予想の研究は、ジョン・ホートン・コンウェイとシモン・ノートン(Simon P. Norton)により種数 0 のモジュラ函数を見つけることに発展した。ジョン・G・トンプソンは、

${\displaystyle q^{-1}+{O}($q)} $q^{-1}+{O}(q)$
という形式に正規化される種数 0 のモジュラ函数が、有限個しか存在しないことを証明した。

別の表現

λ をモジュララムダ函数(modular lambda function)とし、x = λ(1−λ) と置くと

$j(\tau )={\frac {256(1-x)^{3}}{x^{2}}}$$j(\tau )={\frac {256(1-x)^{3}}{x^{2}}}$
を得る。

$\lambda (\tau )={\frac {\theta _{2}^{4}(0,\tau )}{\theta _{3}^{4}(0,\tau )}}=k^{2}(\tau )$$\lambda (\tau )={\frac {\theta _{2}^{4}(0,\tau )}{\theta _{3}^{4}(0,\tau )}}=k^{2}(\tau )$
は、ヤコビのテータ函数 $\theta _{m}$$\theta _{m}$の比率であり、楕円モジュラス $k(\tau )$$k(\tau )$の二乗である。 λ が次の非調和比(cross-ratio)の6つの値で入れ替わるときは、jの値は不変である。

$\left\lbrace {\lambda ,{\frac {1}{1-\lambda }},{\frac {\lambda -1}{\lambda }},{\frac {1}{\lambda }},{\frac {\lambda }{\lambda -1}},1-\lambda }\right\rbrace .$$\left\lbrace {\lambda ,{\frac {1}{1-\lambda }},{\frac {\lambda -1}{\lambda }},{\frac {1}{\lambda }},{\frac {\lambda }{\lambda -1}},1-\lambda }\right\rbrace .$
jの分岐点は {0, 1, ∞} であるので、ベリイ函数(Belyi function)である。

テータ函数による表現

$q=e^{\pi i\tau }$$q=e^{\pi i\tau }$ ︵ノーム︶と定義し直すと、ヤコビのテータ函数

$\vartheta (0;\tau )=\vartheta _{00}(0;\tau )=1+2\sum _{n=1}^{\infty }\left(e^{\pi i\tau }\right)^{n^{2}}=\sum _{n=-\infty }^{\infty }q^{n^{2}}$$\vartheta (0;\tau )=\vartheta _{00}(0;\tau )=1+2\sum _{n=1}^{\infty }\left(e^{\pi i\tau }\right)^{n^{2}}=\sum _{n=-\infty }^{\infty }q^{n^{2}}$
から指標付きテータ函数を導くことができる。次のように置くこととする。

$a=\theta _{2}(0;q)=\vartheta _{10}(0;\tau )$$a=\theta _{2}(0;q)=\vartheta _{10}(0;\tau )$
$b=\theta _{3}(0;q)=\vartheta _{00}(0;\tau )$$b=\theta _{3}(0;q)=\vartheta _{00}(0;\tau )$
$c=\theta _{4}(0;q)=\vartheta _{01}(0;\tau )$$c=\theta _{4}(0;q)=\vartheta _{01}(0;\tau )$
ここに $\theta _{m}$$\theta _{m}$と $\vartheta _{n}$$\vartheta _{n}$は記法を変えたものとした。すると、ヴァイエルシュトラス定数g₂, g₃ とデデキントのエータ函数 η(τ) に対して、

$g_{2}(\tau )={\tfrac {2}{3}}\pi ^{4}\left(a^{8}+b^{8}+c^{8}\right)$$g_{2}(\tau )={\tfrac {2}{3}}\pi ^{4}\left(a^{8}+b^{8}+c^{8}\right)$
$g_{3}(\tau )={\tfrac {4}{27}}\pi ^{6}{\sqrt {\frac {(a^{8}+b^{8}+c^{8})^{3}-54(abc)^{8}}{2}}}$$g_{3}(\tau )={\tfrac {4}{27}}\pi ^{6}{\sqrt {\frac {(a^{8}+b^{8}+c^{8})^{3}-54(abc)^{8}}{2}}}$
$\Delta =g_{2}^{3}-27g_{3}^{2}=(2\pi )^{12}\eta (\tau )^{24}=(2\pi )^{12}\left({\tfrac {1}{2}}abc\right)^{8}$$\Delta =g_{2}^{3}-27g_{3}^{2}=(2\pi )^{12}\eta (\tau )^{24}=(2\pi )^{12}\left({\tfrac {1}{2}}abc\right)^{8}$
となる。このようにすると、j (τ) を早く計算できる形に書き換えることができる。

$j(\tau )=1728{\frac {g_{2}^{3}}{g_{2}^{3}-27g_{3}^{2}}}=32{(a^{8}+b^{8}+c^{8})^{3} \over (abc)^{8}}.$$j(\tau )=1728{\frac {g_{2}^{3}}{g_{2}^{3}-27g_{3}^{2}}}=32{(a^{8}+b^{8}+c^{8})^{3} \over (abc)^{8}}.$
ただし、

$a^{4}-b^{4}+c^{4}=0$$a^{4}-b^{4}+c^{4}=0$
であることに注意する。

代数的定義

今までは、jを複素変数の函数として考えてきたが、楕円曲線の同型類の不変量としては、jを純粋に代数的に定義することもできる。

$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$$y^{2}+a_{1}xy+a_{3}y=x^{3}+a_{2}x^{2}+a_{4}x+a_{6}$
を任意の体の上の平面楕円曲線とすると、

$b_{2}=a_{1}^{2}+4a_{2},\quad b_{4}=a_{1}a_{3}+2a_{4}$$b_{2}=a_{1}^{2}+4a_{2},\quad b_{4}=a_{1}a_{3}+2a_{4}$
$b_{6}=a_{3}^{2}+4a_{6},\quad b_{8}=a_{1}^{2}a_{6}-a_{1}a_{3}a_{4}+a_{2}a_{3}^{2}+4a_{2}a_{6}-a_{4}^{2}$$b_{6}=a_{3}^{2}+4a_{6},\quad b_{8}=a_{1}^{2}a_{6}-a_{1}a_{3}a_{4}+a_{2}a_{3}^{2}+4a_{2}a_{6}-a_{4}^{2}$
$c_{4}=b_{2}^{2}-24b_{4},\quad c_{6}=-b_{2}^{3}+36b_{2}b_{4}-216b_{6}$$c_{4}=b_{2}^{2}-24b_{4},\quad c_{6}=-b_{2}^{3}+36b_{2}b_{4}-216b_{6}$
と定義することができ、

$\Delta =-b_{2}^{2}b_{8}+9b_{2}b_{4}b_{6}-8b_{4}^{3}-27b_{6}^{2}$$\Delta =-b_{2}^{2}b_{8}+9b_{2}b_{4}b_{6}-8b_{4}^{3}-27b_{6}^{2}$
と表すと、これは楕円曲線の判別式を表している。

ここで、楕円曲線の j-不変量を

$j={c_{4}^{3} \over \Delta }$$j={c_{4}^{3} \over \Delta }$
と定義する。

楕円曲線が定義されている体の標数が2もしくは3でない場合に、この定義は

$j=1728{c_{4}^{3} \over c_{4}^{3}-c_{6}^{2}}$$j=1728{c_{4}^{3} \over c_{4}^{3}-c_{6}^{2}}$
と書き直すことができる。

逆函数

j-不変量の逆函数は、超幾何函数 ₂F₁で表すこともできる︵ピカール・フックス方程式(Picard–Fuchs equation)も参照︶。与えられた数値Nに対して 式 j(τ) = N を τ について解くためには、少なくとも4つの方法が知られている。 

方法1: モジュララムダ函数(modular lambda function) λ の6次式を解く方法。

$j(\tau )={\frac {256(1-\lambda (1-\lambda ))^{3}}{(\lambda (1-\lambda ))^{2}}}.$$j(\tau )={\frac {256(1-\lambda (1-\lambda ))^{3}}{(\lambda (1-\lambda ))^{2}}}.$
x = λ(1−λ) とすると6次式はxの3次式となる。すると、λ の6つの値のどれに対しても、

$\tau =i\ {\frac {{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}},1,1-\lambda \right)}{{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}},1,\lambda \right)}}$$\tau =i\ {\frac {{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}},1,1-\lambda \right)}{{}_{2}F_{1}\left({\tfrac {1}{2}},{\tfrac {1}{2}},1,\lambda \right)}}$
となる。 

方法2: γ の4次式を解く方法。

$j(\tau )={\frac {27(1+8\gamma )^{3}}{\gamma (1-\gamma )^{3}}}.$$j(\tau )={\frac {27(1+8\gamma )^{3}}{\gamma (1-\gamma )^{3}}}.$
任意の4つの根に対して、

$\tau ={\frac {i}{\sqrt {3}}}{\frac {{}_{2}F_{1}\left({\tfrac {1}{3}},{\tfrac {2}{3}},1,1-\gamma \right)}{{}_{2}F_{1}\left({\tfrac {1}{3}},{\tfrac {2}{3}},1,\gamma \right)}}$$\tau ={\frac {i}{\sqrt {3}}}{\frac {{}_{2}F_{1}\left({\tfrac {1}{3}},{\tfrac {2}{3}},1,1-\gamma \right)}{{}_{2}F_{1}\left({\tfrac {1}{3}},{\tfrac {2}{3}},1,\gamma \right)}}$
となる。

方法3: β の3次式を解く方法。

$j(\tau )={\frac {64(1+3\beta )^{3}}{\beta (1-\beta )^{2}}}.$$j(\tau )={\frac {64(1+3\beta )^{3}}{\beta (1-\beta )^{2}}}.$
すると、任意の3つの根に対し、

$\tau ={\frac {i}{\sqrt {2}}}{\frac {{}_{2}F_{1}\left({\tfrac {1}{4}},{\tfrac {3}{4}},1,1-\beta \right)}{{}_{2}F_{1}\left({\tfrac {1}{4}},{\tfrac {3}{4}},1,\beta \right)}}$$\tau ={\frac {i}{\sqrt {2}}}{\frac {{}_{2}F_{1}\left({\tfrac {1}{4}},{\tfrac {3}{4}},1,1-\beta \right)}{{}_{2}F_{1}\left({\tfrac {1}{4}},{\tfrac {3}{4}},1,\beta \right)}}$
となる。

方法4: α の2次式を解く方法。

$j(\tau )={\frac {1728}{4\alpha (1-\alpha )}}.$$j(\tau )={\frac {1728}{4\alpha (1-\alpha )}}.$
すると、

$\tau =i\ {\frac {{}_{2}F_{1}\left({\tfrac {1}{6}},{\tfrac {5}{6}},1,1-\alpha \right)}{{}_{2}F_{1}\left({\tfrac {1}{6}},{\tfrac {5}{6}},1,\alpha \right)}}$$\tau =i\ {\frac {{}_{2}F_{1}\left({\tfrac {1}{6}},{\tfrac {5}{6}},1,1-\alpha \right)}{{}_{2}F_{1}\left({\tfrac {1}{6}},{\tfrac {5}{6}},1,\alpha \right)}}$
となる。

2つの根は τ と -1/τ であるが、j (τ) = j (-1/τ) であるために、どの α を選んでも差異はない。後半3つの方法は、ラマヌジャンの交代基底についての楕円函数論で発見された。

逆函数は、これらの根の比率が有界でないにもかかわらず、楕円函数の周期の高精度な計算を通して、うまく適用することが可能である。また、関連する帰結として、2のべきの大きさをもつ虚数軸上の点でjの値が二次の根となることを通して︵逆関数を︶表すことができる︵このようにして、定規とコンパスによる作図が可能となる︶。レベルが2のモジュラ函数は3次式であるので、この結果は自明ではない。

π公式

チュダノフスキー兄弟(Chudnovsky brothers)は、1987年に、

${\frac {1}{\pi }}={\frac {12}{640320^{3/2}}}\sum _{k=0}^{\infty }{\frac {(6k)!(163\cdot 3344418k+13591409)}{(3k)!(k!)^{3}(-640320)^{3k}}}$${\frac {1}{\pi }}={\frac {12}{640320^{3/2}}}\sum _{k=0}^{\infty }{\frac {(6k)!(163\cdot 3344418k+13591409)}{(3k)!(k!)^{3}(-640320)^{3k}}}$
を発見し、$j{\big (}{\tfrac {1+{\sqrt {-163}}}{2}}{\big )}=-640320^{3}$$j{\big (}{\tfrac {1+{\sqrt {-163}}}{2}}{\big )}=-640320^{3}$ という事実を示すことに使用した。同様な公式は、ラマヌジャン・佐藤級数(Ramanujan-Sato series)を参照。

ボーチャーズの積公式

次はリチャード・ボーチャーズによって発見された。

$j(\tau )-j(\tau ')={1 \over q}\prod _{n,m=1}^{\infty }(1-q^{n}{q'}^{m})^{c_{nm}}$$j(\tau )-j(\tau ')={1 \over q}\prod _{n,m=1}^{\infty }(1-q^{n}{q'}^{m})^{c_{nm}}$
である︵ここでc_nはj関数のq展開におけるq^nの係数︶．

特殊値

j-不変量は、基本領域(fundamental domain)の﹁角﹂

${\tfrac {1}{2}}\left(1+i{\sqrt {3}}\right)$${\tfrac {1}{2}}\left(1+i{\sqrt {3}}\right)$
では 0 となる。

以下に、いくつかの特殊値を示す︵J = j/1728 を使って表示している︶。

${\displaystyle {\begin{aligned}J($i)&=J\left({\tfrac {1+i}{2}}\right)=1\\J\left({\sqrt {2}}i\right)&={\big (}{\tfrac {5}{3}}{\big )}^{3}\\J(2i)&={\big (}{\tfrac {11}{2}}{\big )}^{3}\\J\left(2{\sqrt {2}}i\right)&={\tfrac {125}{216}}\left(19+13{\sqrt {2}}\right)^{3}\\J(4i)&={\tfrac {1}{64}}\left(724+513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2i}{2}}\right)&={\tfrac {1}{64}}\left(724-513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2{\sqrt {2}}i}{3}}\right)&={\tfrac {125}{216}}\left(19-13{\sqrt {2}}\right)^{3}\\J(3i)&={\tfrac {1}{27}}\left(2+{\sqrt {3}}\right)^{2}\left(21+20{\sqrt {3}}\right)^{3}\\J\left(2{\sqrt {3}}i\right)&={\tfrac {125}{16}}\left(30+17{\sqrt {3}}\right)^{3}\\J\left({\tfrac {1+7{\sqrt {3}}i}{2}}\right)&=-{\tfrac {64000}{7}}\left(651+142{\sqrt {21}}\right)^{3}\\J\left({\tfrac {1+3{\sqrt {11}}i}{10}}\right)&={\tfrac {64}{27}}\left(23-4{\sqrt {33}}\right)^{2}\left(-77+15{\sqrt {33}}\right)^{3}\\J\left({\sqrt {21}}i\right)&={\tfrac {1}{128}}\left(3+{\sqrt {7}}\right)^{5}\left(17+7{\sqrt {3}}+59{\sqrt {7}}+35{\sqrt {21}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{1}}\right)&={\tfrac {1}{4}}\left(7+5{\sqrt {2}}+3{\sqrt {5}}+2{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}+12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{2}}\right)&={\tfrac {1}{4}}\left(7+5{\sqrt {2}}-3{\sqrt {5}}-2{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}-12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{5}}\right)&={\tfrac {1}{4}}\left(7-5{\sqrt {2}}+3{\sqrt {5}}-2{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}+12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{10}}\right)&={\tfrac {1}{4}}\left(7-5{\sqrt {2}}-3{\sqrt {5}}+2{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}-12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {1+{\sqrt {31}}i}{2}}\right)&=\left(1-\left(1+{\frac {\sqrt {19}}{2}}\left({\sqrt {\tfrac {13-{\sqrt {93}}}{13+{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}+{\sqrt {27}}}{{\sqrt {31}}-{\sqrt {27}}}}}+{\sqrt {\tfrac {13+{\sqrt {93}}}{13-{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}-{\sqrt {27}}}{{\sqrt {31}}+{\sqrt {27}}}}}\right)\right)^{2}\right)^{3}\\J(5i)&=\left(1+{\tfrac {9}{4}}{\sqrt {5}}\left(13+5{\sqrt {5}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i+1}{2}}\right)&=\left(1-{\tfrac {9}{4}}{\sqrt {5}}\left(13-5{\sqrt {5}}\right)^{2}\right)^{3}\\J(6i)&={\tfrac {1}{216}}\left(2+{\sqrt {3}}\right)^{10}\left(231+380{\sqrt {3}}+\left(204+158{\sqrt {3}}\right){\sqrt[{4}]{12}}\right)^{3}\\J({\sqrt {70}}i)&=\left(1+{\tfrac {9}{4}}\left(303+220{\sqrt {2}}+139{\sqrt {5}}+96{\sqrt {10}}\right)^{2}\right)^{3}\\J({\sqrt {94}}i)&=\left(1+{\tfrac {9}{8192}}\left(3+2{\sqrt {2}}+{\sqrt {9+8{\sqrt {2}}}}\right)^{8}\left(8+\left(-1-{\sqrt {2}}+{\sqrt {9+8{\sqrt {2}}}}\right)\left(-2+2{\sqrt {2}}+{\sqrt {3+4{\sqrt {2}}+3{\sqrt {9+8{\sqrt {2}}}}}}\right)\right)^{2}\right)^{3}\\J(7i)&=\left(1+{\tfrac {9}{32}}{\sqrt[{4}]{28}}\left(3+{\sqrt {7}}\right)^{3}\left(13+3{\sqrt {7}}+\left(6+{\sqrt {7}}\right){\sqrt[{4}]{28}}\right)^{2}\right)^{3}\\J(8i)&=\left(1+{\tfrac {9}{4}}{\sqrt[{4}]{2}}\left(1+{\sqrt {2}}\right)\left(123+104{\sqrt[{4}]{2}}+88{\sqrt {2}}+73{\sqrt[{4}]{8}}\right)^{2}\right)^{3}\\J(10i)&=\left(1+{\tfrac {9}{8}}\left(2402+1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}+719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i}{2}}\right)&=\left(1+{\tfrac {9}{8}}\left(2402-1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}-719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J({\sqrt {130}}i)&=\left(1+{\tfrac {9}{4}}\left(7392+3289{\sqrt {5}}+2040{\sqrt {13}}+917{\sqrt {65}}\right)^{2}\right)^{3}\\J({\sqrt {190}}i)&=\left(1+18\left(31570+22323{\sqrt {2}}+14139{\sqrt {5}}+9998{\sqrt {10}}\right)^{2}\right)^{3}\\J(2{\sqrt {58}}i)&=\left(1+{\tfrac {9}{256}}\left(1+{\sqrt {2}}\right)^{5}\left(5+{\sqrt {29}}\right)^{5}\left(793+907{\sqrt {2}}+237{\sqrt {29}}+103{\sqrt {58}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1435}}i}{2}}\right)&=\left(1-9\left(9892538+4424079{\sqrt {5}}+1544955{\sqrt {41}}+690925{\sqrt {205}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1555}}i}{2}}\right)&=\left(1-9\left(22297077+9971556{\sqrt {5}}+\left(3571365+1597163{\sqrt {5}}\right){\sqrt {\tfrac {31+21{\sqrt {5}}}{2}}}\right)^{2}\right)^{3}\\\end{aligned}}} ${\begin{aligned}J(i)&=J\left({\tfrac {1+i}{2}}\right)=1\\J\left({\sqrt {2}}i\right)&={\big (}{\tfrac {5}{3}}{\big )}^{3}\\J(2i)&={\big (}{\tfrac {11}{2}}{\big )}^{3}\\J\left(2{\sqrt {2}}i\right)&={\tfrac {125}{216}}\left(19+13{\sqrt {2}}\right)^{3}\\J(4i)&={\tfrac {1}{64}}\left(724+513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2i}{2}}\right)&={\tfrac {1}{64}}\left(724-513{\sqrt {2}}\right)^{3}\\J\left({\tfrac {1+2{\sqrt {2}}i}{3}}\right)&={\tfrac {125}{216}}\left(19-13{\sqrt {2}}\right)^{3}\\J(3i)&={\tfrac {1}{27}}\left(2+{\sqrt {3}}\right)^{2}\left(21+20{\sqrt {3}}\right)^{3}\\J\left(2{\sqrt {3}}i\right)&={\tfrac {125}{16}}\left(30+17{\sqrt {3}}\right)^{3}\\J\left({\tfrac {1+7{\sqrt {3}}i}{2}}\right)&=-{\tfrac {64000}{7}}\left(651+142{\sqrt {21}}\right)^{3}\\J\left({\tfrac {1+3{\sqrt {11}}i}{10}}\right)&={\tfrac {64}{27}}\left(23-4{\sqrt {33}}\right)^{2}\left(-77+15{\sqrt {33}}\right)^{3}\\J\left({\sqrt {21}}i\right)&={\tfrac {1}{128}}\left(3+{\sqrt {7}}\right)^{5}\left(17+7{\sqrt {3}}+59{\sqrt {7}}+35{\sqrt {21}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{1}}\right)&={\tfrac {1}{4}}\left(7+5{\sqrt {2}}+3{\sqrt {5}}+2{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}+12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{2}}\right)&={\tfrac {1}{4}}\left(7+5{\sqrt {2}}-3{\sqrt {5}}-2{\sqrt {10}}\right)^{4}\left(55+30{\sqrt {2}}-12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{5}}\right)&={\tfrac {1}{4}}\left(7-5{\sqrt {2}}+3{\sqrt {5}}-2{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}+12{\sqrt {5}}-10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {{\sqrt {30}}i}{10}}\right)&={\tfrac {1}{4}}\left(7-5{\sqrt {2}}-3{\sqrt {5}}+2{\sqrt {10}}\right)^{4}\left(55-30{\sqrt {2}}-12{\sqrt {5}}+10{\sqrt {10}}\right)^{3}\\J\left({\tfrac {1+{\sqrt {31}}i}{2}}\right)&=\left(1-\left(1+{\frac {\sqrt {19}}{2}}\left({\sqrt {\tfrac {13-{\sqrt {93}}}{13+{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}+{\sqrt {27}}}{{\sqrt {31}}-{\sqrt {27}}}}}+{\sqrt {\tfrac {13+{\sqrt {93}}}{13-{\sqrt {93}}}}}\cdot {\sqrt[{3}]{\tfrac {{\sqrt {31}}-{\sqrt {27}}}{{\sqrt {31}}+{\sqrt {27}}}}}\right)\right)^{2}\right)^{3}\\J(5i)&=\left(1+{\tfrac {9}{4}}{\sqrt {5}}\left(13+5{\sqrt {5}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i+1}{2}}\right)&=\left(1-{\tfrac {9}{4}}{\sqrt {5}}\left(13-5{\sqrt {5}}\right)^{2}\right)^{3}\\J(6i)&={\tfrac {1}{216}}\left(2+{\sqrt {3}}\right)^{10}\left(231+380{\sqrt {3}}+\left(204+158{\sqrt {3}}\right){\sqrt[{4}]{12}}\right)^{3}\\J({\sqrt {70}}i)&=\left(1+{\tfrac {9}{4}}\left(303+220{\sqrt {2}}+139{\sqrt {5}}+96{\sqrt {10}}\right)^{2}\right)^{3}\\J({\sqrt {94}}i)&=\left(1+{\tfrac {9}{8192}}\left(3+2{\sqrt {2}}+{\sqrt {9+8{\sqrt {2}}}}\right)^{8}\left(8+\left(-1-{\sqrt {2}}+{\sqrt {9+8{\sqrt {2}}}}\right)\left(-2+2{\sqrt {2}}+{\sqrt {3+4{\sqrt {2}}+3{\sqrt {9+8{\sqrt {2}}}}}}\right)\right)^{2}\right)^{3}\\J(7i)&=\left(1+{\tfrac {9}{32}}{\sqrt[{4}]{28}}\left(3+{\sqrt {7}}\right)^{3}\left(13+3{\sqrt {7}}+\left(6+{\sqrt {7}}\right){\sqrt[{4}]{28}}\right)^{2}\right)^{3}\\J(8i)&=\left(1+{\tfrac {9}{4}}{\sqrt[{4}]{2}}\left(1+{\sqrt {2}}\right)\left(123+104{\sqrt[{4}]{2}}+88{\sqrt {2}}+73{\sqrt[{4}]{8}}\right)^{2}\right)^{3}\\J(10i)&=\left(1+{\tfrac {9}{8}}\left(2402+1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}+719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J\left({\tfrac {5i}{2}}\right)&=\left(1+{\tfrac {9}{8}}\left(2402-1607{\sqrt[{4}]{5}}+1074{\sqrt[{4}]{25}}-719{\sqrt[{4}]{125}}\right)^{2}\right)^{3}\\J({\sqrt {130}}i)&=\left(1+{\tfrac {9}{4}}\left(7392+3289{\sqrt {5}}+2040{\sqrt {13}}+917{\sqrt {65}}\right)^{2}\right)^{3}\\J({\sqrt {190}}i)&=\left(1+18\left(31570+22323{\sqrt {2}}+14139{\sqrt {5}}+9998{\sqrt {10}}\right)^{2}\right)^{3}\\J(2{\sqrt {58}}i)&=\left(1+{\tfrac {9}{256}}\left(1+{\sqrt {2}}\right)^{5}\left(5+{\sqrt {29}}\right)^{5}\left(793+907{\sqrt {2}}+237{\sqrt {29}}+103{\sqrt {58}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1435}}i}{2}}\right)&=\left(1-9\left(9892538+4424079{\sqrt {5}}+1544955{\sqrt {41}}+690925{\sqrt {205}}\right)^{2}\right)^{3}\\J\left({\tfrac {1+{\sqrt {1555}}i}{2}}\right)&=\left(1-9\left(22297077+9971556{\sqrt {5}}+\left(3571365+1597163{\sqrt {5}}\right){\sqrt {\tfrac {31+21{\sqrt {5}}}{2}}}\right)^{2}\right)^{3}\\\end{aligned}}$
2014年にはいくつかの特殊値が計算された。

${\begin{aligned}J\left({\tfrac {5i+2}{4}}\right)&=\left(1-{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}+1479{\sqrt {5}}-3072{\sqrt {10}}-{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}+3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {10i+1}{2}}\right)&=\left(1-{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}+1479{\sqrt {5}}-3072{\sqrt {10}}+{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}+3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {5i}{4}}\right)&=\left(1+{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}+1479{\sqrt {5}}+3072{\sqrt {10}}-{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}+3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Big )}^{2}\right)^{3}\\J(20i)&=\left(1+{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}+1479{\sqrt {5}}+3072{\sqrt {10}}+{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}+3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\end{aligned}}$${\begin{aligned}J\left({\tfrac {5i+2}{4}}\right)&=\left(1-{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}+1479{\sqrt {5}}-3072{\sqrt {10}}-{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}+3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {10i+1}{2}}\right)&=\left(1-{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}+1479{\sqrt {5}}-3072{\sqrt {10}}+{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}+3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {5i}{4}}\right)&=\left(1+{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}+1479{\sqrt {5}}+3072{\sqrt {10}}-{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}+3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Big )}^{2}\right)^{3}\\J(20i)&=\left(1+{\tfrac {9\left(1+{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}+1479{\sqrt {5}}+3072{\sqrt {10}}+{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}+3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\end{aligned}}$
これ以前に示したすべての値は実数である。複素共役のペアは、$J(10i)$$J(10i)$ と $J(5i/2)$$J(5i/2)$に対し、参考文献のように値に沿って、上記のように対称的になっていると推察される。

${\begin{aligned}J\left({\tfrac {5i\pm 1}{4}}\right)&=\left(1-{\tfrac {9}{8}}\left((2402-1074{\sqrt {5}})i\pm (1607-719{\sqrt {5}}){\sqrt[{4}]{5}}\right)^{2}\right)^{3}\end{aligned}}$${\begin{aligned}J\left({\tfrac {5i\pm 1}{4}}\right)&=\left(1-{\tfrac {9}{8}}\left((2402-1074{\sqrt {5}})i\pm (1607-719{\sqrt {5}}){\sqrt[{4}]{5}}\right)^{2}\right)^{3}\end{aligned}}$
4つの特殊値は、2つの複素共役のペアにより与えられる。

${\begin{aligned}J\left({\tfrac {4\left(5i\pm 1\right)}{13}}\right)=\left(1-{\tfrac {9\left(1-{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485-762{\sqrt {2}}-1479{\sqrt {5}}+3072{\sqrt {10}}\pm i{\sqrt[{4}]{5}}\left(178-2221{\sqrt {2}}-3148{\sqrt {5}}+1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\\J\left({\tfrac {5\left(4i\pm 1\right)}{17}}\right)=\left(1+{\tfrac {9\left(1-{\sqrt {5}}\right)^{38}}{2^{41}{\sqrt {2}}}}{\Bigl (}7485+762{\sqrt {2}}-1479{\sqrt {5}}-3072{\sqrt {10}}\pm i{\sqrt[{4}]{5}}\left(178+2221{\sqrt {2}}-3148{\sqrt {5}}-1289{\sqrt {10}}\right){\Bigr )}^{2}\right)^{3}\end{aligned}}$

参考文献

• Apostol, Tom M. (1976), Modular functions and Dirichlet Series in Number Theory, Graduate Texts in Mathematics, 41, New York: Springer-Verlag, MR0422157 . Provides a very readable introduction and various interesting identities.
  • Apostol, Tom M. (1990), Modular functions and Dirichlet Series in Number Theory (2nd ed.), ISBN 0-387-97127-0, MR1027834 
• Berndt, Bruce C.; Chan, Heng Huat (1999), “Ramanujan and the modular j-invariant”, Canadian Mathematical Bulletin 42 (4): 427–440, doi:10.4153/CMB-1999-050-1, MR1727340, http://www.journals.cms.math.ca/cgi-bin/vault/public/view/berndt7376/body/PDF/berndt7376.pdf . Provides a variety of interesting algebraic identities, including the inverse as a hypergeometric series.
• Cox, David A. (1989), Primes of the Form x^2 + ny^2: Fermat, Class Field Theory, and Complex Multiplication, New York: Wiley-Interscience Publication, John Wiley & Sons Inc., MR1028322  Introduces the j-invariant and discusses the related class field theory.
• Conway, John Horton; Norton, Simon (1979), “Monstrous moonshine”, Bulletin of the London Mathematical Society 11 (3): 308–339, doi:10.1112/blms/11.3.308, MR0554399 . Includes a list of the 175 genus-zero modular functions.
• Rankin, Robert A. (1977), Modular forms and functions, Cambridge: Cambridge University Press, ISBN 0-521-21212-X, MR0498390 . Provides a short review in the context of modular forms.
• Schneider, Theodor (1937), “Arithmetische Untersuchungen elliptischer Integrale”, Math. Annalen 113: 1–13, doi:10.1007/BF01571618, MR1513075 .