

|
→Incompressible Euler equations with constant and uniform density: Small wording change
Tags: Mobile edit Mobile web edit
|
Remove erroneous whitespace in the first paragraph
|
||
| (18 intermediate revisions by 16 users not shown) | |||
| Line 4: | Line 4: | ||
[[File:Flow around a wing.gif|thumb|Flow around a wing. This incompressible flow satisfies the Euler equations.]] |
[[File:Flow around a wing.gif|thumb|Flow around a wing. This incompressible flow satisfies the Euler equations.]] |
||
In [[fluid dynamics]], the '''Euler equations''' are a set of |
In [[fluid dynamics]], the '''Euler equations''' are a set of [[partial differential equation]]s governing [[adiabatic process|adiabatic]] and [[inviscid flow]]. They are named after [[Leonhard Euler]]. In particular, they correspond to the [[Navier–Stokes equations]] with zero [[viscosity]] and zero [[thermal conductivity]].{{sfn|Toro|1999|p= 24}} |
||
The Euler equations can be applied to [[incompressible flow|incompressible]] |
The Euler equations can be applied to [[incompressible flow|incompressible]] and [[compressible flow]]s. The incompressible Euler equations consist of [[Cauchy momentum equation|Cauchy equations]] for conservation of mass and balance of momentum, together with the incompressibility condition that the [[flow velocity]] is a [[solenoidal field]]. The compressible Euler equations consist of equations for conservation of mass, balance of momentum, and balance of energy, together with a suitable [[constitutive equation]] for the specific energy density of the fluid. Historically, only the equations of conservation of mass and balance of momentum were derived by Euler. However, fluid dynamics literature often refers to the full set of the compressible Euler equations – including the energy equation – as "the compressible Euler equations".{{sfn|Anderson|1995|p=}} |
||
The mathematical characters of the incompressible and compressible Euler equations are rather different. For constant fluid density, the incompressible equations can be written as a quasilinear [[advection]] equation for the fluid velocity together with an elliptic [[Poisson's equation]] for the pressure. On the other hand, the compressible Euler equations form a quasilinear [[hyperbolic partial differential equation|hyperbolic]] system of [[conservation equation]]s. |
The mathematical characters of the incompressible and compressible Euler equations are rather different. For constant fluid density, the incompressible equations can be written as a quasilinear [[advection]] equation for the fluid velocity together with an elliptic [[Poisson's equation]] for the pressure. On the other hand, the compressible Euler equations form a quasilinear [[hyperbolic partial differential equation|hyperbolic]] system of [[conservation equation]]s. |
||
| Line 24: | Line 24: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Incompressible Euler equations with constant and uniform density''' |
|title='''Incompressible Euler equations with constant and uniform density'''<br/>(''convective or Lagrangian form'') |
||
|equation=<math>\left\{\begin{align} |
|equation=<math>\left\{\begin{align} |
||
{D\mathbf{u} \over Dt} &= -\nabla w + \mathbf{g} \\ |
{D\mathbf{u} \over Dt} &= -\nabla w + \mathbf{g} \\ |
||
| Line 37: | Line 37: | ||
where: |
where: |
||
*<math>\mathbf u</math> is the [[flow velocity]] [[Vector (geometric)|vector]], with components in an ''N''-dimensional space <math>u_1, u_2, \dots, u_N</math>, |
*<math>\mathbf u</math> is the [[flow velocity]] [[Vector (geometric)|vector]], with components in an ''N''-dimensional space <math>u_1, u_2, \dots, u_N</math>, |
||
*<math>{D\ |
*<math>\frac{D\boldsymbol\Phi}{Dt} = \frac{\partial\boldsymbol\Phi}{\partial t} + \mathbf v\cdot \nabla \boldsymbol\Phi</math>, for a generic function (or field) <math>\boldsymbol\Phi</math> denotes its [[material derivative]] in time with respect to the advective field <math>\mathbf v</math> and |
||
*<math>\nabla w</math> is the [[gradient]] of the specific (with the sense of ''per unit mass'') [[thermodynamic work]], the internal [[Linear differential equation|source term]], and |
*<math>\nabla w</math> is the [[gradient]] of the specific (with the sense of ''per unit mass'') [[thermodynamic work]], the internal [[Linear differential equation|source term]], and |
||
*<math>\nabla \cdot \mathbf u</math> is the flow velocity [[divergence]]. |
*<math>\nabla \cdot \mathbf u</math> is the flow velocity [[divergence]]. |
||
| Line 43: | Line 43: | ||
The first equation is the [[Cauchy momentum equation|Euler momentum equation]] with uniform density (for this equation it could also not be constant in time). By expanding the [[material derivative]], the equations become: |
The first equation is the [[Cauchy momentum equation|Euler momentum equation]] with uniform density (for this equation it could also not be constant in time). By expanding the [[material derivative]], the equations become: |
||
<math display="block">\left\{\begin{align} |
|||
:<math>\left\{\begin{align} |
|||
{\partial\mathbf{u} \over \partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} &= -\nabla w + \mathbf{g} \\ |
{\partial\mathbf{u} \over \partial t} + (\mathbf{u} \cdot \nabla) \mathbf{u} &= -\nabla w + \mathbf{g} \\ |
||
\nabla \cdot \mathbf{u} &= 0 |
\nabla \cdot \mathbf{u} &= 0 |
||
| Line 50: | Line 49: | ||
In fact for a flow with uniform density <math>\rho_0</math> the following identity holds: |
In fact for a flow with uniform density <math>\rho_0</math> the following identity holds: |
||
<math display="block">\nabla w \equiv \nabla \left(\frac p {\rho_0} \right) = \frac 1 {\rho_0} \nabla p </math> |
|||
:<math>\nabla w \equiv \nabla \left(\frac p {\rho_0} \right) = \frac 1 {\rho_0} \nabla p </math> |
|||
where <math>p</math> is the mechanic [[pressure]]. The second equation is the [[incompressible flow|incompressible constraint]], stating the flow velocity is a [[solenoidal field]] (the order of the equations is not causal, but underlines the fact that the incompressible constraint is not a degenerate form of the [[continuity equation]], but rather of the energy equation, as it will become clear in the following). Notably, the [[continuity equation]] would be required also in this incompressible case as an additional third equation in case of density varying in time ''or'' varying in space. For example, with density uniform but varying in time, the continuity equation to be added to the above set would correspond to: |
where <math>p</math> is the mechanic [[pressure]]. The second equation is the [[incompressible flow|incompressible constraint]], stating the flow velocity is a [[solenoidal field]] (the order of the equations is not causal, but underlines the fact that the incompressible constraint is not a degenerate form of the [[continuity equation]], but rather of the energy equation, as it will become clear in the following). Notably, the [[continuity equation]] would be required also in this incompressible case as an additional third equation in case of density varying in time ''or'' varying in space. For example, with density uniform but varying in time, the continuity equation to be added to the above set would correspond to: |
||
<math display="block">\frac{\partial \rho}{\partial t} = 0 </math> |
|||
So the case of constant '''and''' uniform density is the only one not requiring the continuity equation as additional equation regardless of the presence or absence of the incompressible constraint. In fact, the case of incompressible Euler equations with constant and uniform density discussed here is a [[toy model]] featuring only two simplified equations, so it is ideal for didactical purposes even if with limited physical relevance. |
|||
:<math>\frac{\partial \rho}{\partial t} = 0 </math> |
|||
So the case of constant '''and''' uniform density is the only one not requiring the continuity equation as additional equation regardless of the presence or absence of the incompressible constraint. In fact, the case of incompressible Euler equations with constant and uniform density discussed here is a [[toy model]] featuring only two simplified equations, so it is ideal for didactical purposes even if with limited physical relevancy. |
|||
The equations above thus represent respectively [[conservation of mass]] (1 scalar equation) and [[conservation of momentum|momentum]] (1 vector equation containing <math>N</math> scalar components, where <math>N</math> is the physical dimension of the space of interest). Flow velocity and pressure are the so-called ''physical variables''.{{sfn|Toro|1999|p= 24}} |
The equations above thus represent respectively [[conservation of mass]] (1 scalar equation) and [[conservation of momentum|momentum]] (1 vector equation containing <math>N</math> scalar components, where <math>N</math> is the physical dimension of the space of interest). Flow velocity and pressure are the so-called ''physical variables''.{{sfn|Toro|1999|p= 24}} |
||
| Line 71: | Line 67: | ||
===Properties=== |
===Properties=== |
||
Although Euler first presented these equations in 1755, many fundamental questions about them remain unanswered. |
Although Euler first presented these equations in 1755, many fundamental questions or concepts about them remain unanswered. |
||
In three space dimensions, in certain simplified scenarios, the Euler equations produce singularities.<ref> |
In three space dimensions, in certain simplified scenarios, the Euler equations produce singularities.<ref>{{Cite journal |last=Elgindi |first=Tarek M. |date=2021-11-01 |title=Finite-time singularity formation for $C^{1,\alpha}$ solutions to the incompressible Euler equations on $\mathbb{R}^3$ |url=https://projecteuclid.org/journals/annals-of-mathematics/volume-194/issue-3/Finite-time-singularity-formation-for-C1alpha-solutions-to-the-incompressible/10.4007/annals.2021.194.3.2.full |journal=Annals of Mathematics |volume=194 | arxiv = 1904.04795 |issue=3 |doi=10.4007/annals.2021.194.3.2 |issn=0003-486X}}</ref> |
||
Smooth solutions of the free (in the sense of without source term: g=0) equations satisfy the conservation of specific kinetic energy: |
Smooth solutions of the free (in the sense of without source term: g=0) equations satisfy the conservation of specific kinetic energy: |
||
<math display="block">{\partial \over\partial t} \left(\frac{1}{2} u^2 \right) + \nabla \cdot \left(u^2 \mathbf u + w \mathbf u\right) = 0 </math> |
|||
In the one-dimensional case without the source term (both pressure gradient and external force), the momentum equation becomes the inviscid [[Burgers' equation]]: |
|||
: <math>{\partial \over\partial t} \left(\frac{1}{2} u^2 \right) + \nabla \cdot \left(u^2 \mathbf u + w \mathbf u\right) = 0 </math> |
|||
<math display="block">{\partial u \over\partial t}+ u {\partial u \over\partial x} = 0</math> |
|||
This model equation gives many insights into Euler equations. |
|||
In the one dimensional case without the source term (both pressure gradient and external force), the momentum equation becomes the inviscid [[Burgers equation]]: |
|||
: <math>{\partial u \over\partial t}+ u {\partial u \over\partial x} = 0</math> |
|||
This is a model equation giving many insights on Euler equations. |
|||
===Nondimensionalisation=== |
===Nondimensionalisation=== |
||
{{See also|Cauchy momentum equation#Nondimensionalisation}}{{Unreferenced section|date=April 2021}} |
{{See also|Cauchy momentum equation#Nondimensionalisation}} |
||
{{Unreferenced section|date=April 2021}} |
|||
In order to make the equations dimensionless, a characteristic length <math>r_0</math>, and a characteristic velocity <math>u_0</math>, need to be defined. These should be chosen such that the dimensionless variables are all of order one. The following dimensionless variables are thus obtained: |
In order to make the equations dimensionless, a characteristic length <math>r_0</math>, and a characteristic velocity <math>u_0</math>, need to be defined. These should be chosen such that the dimensionless variables are all of order one. The following dimensionless variables are thus obtained: |
||
<math display="block">\begin{align} |
|||
u^* & \equiv \frac{u}{u_0}, & |
|||
: <math>\begin{align} |
|||
u^* & \equiv \frac{u}{u_0}, \\[5pt] |
|||
r^* & \equiv \frac{r}{r_0}, \\[5pt] |
r^* & \equiv \frac{r}{r_0}, \\[5pt] |
||
t^* & \equiv \frac{u_0}{r_0} t, |
t^* & \equiv \frac{u_0}{r_0} t, & |
||
p^* & \equiv \frac{w}{u_0^2}, \\[5pt] |
p^* & \equiv \frac{w}{u_0^2}, \\[5pt] |
||
\nabla^* & \equiv r_0 \nabla |
\nabla^* & \equiv r_0 \nabla |
||
\end{align}</math> |
\end{align}</math> |
||
and of the field [[unit vector]]: |
and of the field [[unit vector]]: |
||
<math display="block">\hat{\mathbf g}\equiv \frac {\mathbf g} g, </math> |
|||
: <math>\hat{\mathbf g}\equiv \frac {\mathbf g} g, </math> |
|||
Substitution of these inversed relations in Euler equations, defining the [[Froude number]], yields (omitting the * at apix): |
Substitution of these inversed relations in Euler equations, defining the [[Froude number]], yields (omitting the * at apix): |
||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Incompressible Euler equations with constant and uniform density''' |
|title='''Incompressible Euler equations with constant and uniform density'''<br/>(''nondimensional form'') |
||
|equation=<math>\left\{\begin{align} |
|equation=<math>\left\{\begin{align} |
||
{D\mathbf{u} \over Dt} &= -\nabla w + \frac{1}{\mathrm{Fr}} \hat{\mathbf{g}} \\ |
{D\mathbf{u} \over Dt} &= -\nabla w + \frac{1}{\mathrm{Fr}} \hat{\mathbf{g}} \\ |
||
| Line 123: | Line 115: | ||
The '''free Euler equations are conservative''', in the sense they are equivalent to a conservation equation: |
The '''free Euler equations are conservative''', in the sense they are equivalent to a conservation equation: |
||
<math display="block"> |
|||
:<math> |
|||
\frac{\partial \mathbf y}{\partial t}+ \nabla \cdot \mathbf F ={\mathbf 0}, |
\frac{\partial \mathbf y}{\partial t}+ \nabla \cdot \mathbf F ={\mathbf 0}, |
||
</math> |
</math> |
||
or simply in Einstein notation: |
or simply in Einstein notation: |
||
<math display="block"> |
|||
:<math> |
|||
\frac{\partial y_j}{\partial t}+ |
\frac{\partial y_j}{\partial t}+ |
||
\frac{\partial f_{ij}}{\partial r_i}= 0_i, |
\frac{\partial f_{ij}}{\partial r_i}= 0_i, |
||
</math> |
</math> |
||
where the conservation quantity <math>\mathbf y</math> in this case is a vector, and <math>\mathbf F</math> is a [[flux]] matrix. This can be simply proved. |
where the conservation quantity <math>\mathbf y</math> in this case is a vector, and <math>\mathbf F</math> is a [[flux]] matrix. This can be simply proved. |
||
| Line 140: | Line 128: | ||
|Demonstration of the conservation form |
|Demonstration of the conservation form |
||
|First, the following identities hold: |
|First, the following identities hold: |
||
<math display="block">\nabla \cdot (w \mathbf I) = \mathbf I \cdot \nabla w + w \nabla \cdot \mathbf I = \nabla w </math> |
|||
|
<math display="block">\mathbf u \cdot \nabla \cdot \mathbf u = \nabla \cdot (\mathbf u \otimes \mathbf u)</math> |
||
where <math>\otimes</math> denotes the [[outer product]]. The same identities expressed in [[Einstein notation]] are: |
|||
:<math>\mathbf u \cdot \nabla \cdot \mathbf u = \nabla \cdot (\mathbf u \otimes \mathbf u)</math> |
|||
<math display="block">\partial_i\left(w \delta_{ij}\right) = \delta_{ij} \partial_i w + w \partial_i \delta_{ij} = \delta_{ij} \partial_i w = \partial_j w</math> |
|||
<math display="block">u_j \partial_i u_i = \partial_i \left(u_i u_j\right)</math> |
|||
where ''<math>\otimes</math>'' denotes the [[outer product]]. The same identities expressed in [[Einstein notation]] are: |
|||
where {{mvar|I}} is the [[identity matrix]] with dimension {{mvar|N}} and {{mvar|δ<sub>ij</sub>}} its general element, the Kroenecker delta. |
|||
:<math>\partial_i\left(w \delta_{ij}\right) = \delta_{ij} \partial_i w + w \partial_i \delta_{ij} = \delta_{ij} \partial_i w = \partial_j w</math> |
|||
:<math>u_j \partial_i u_i = \partial_i \left(u_i u_j\right)</math> |
|||
where I is the [[identity matrix]] with dimension N and δ<sub>ij</sub> its general element, the Kroenecker delta. |
|||
Thanks to these vector identities, the incompressible Euler equations with constant and uniform density and without external field can be put in the so-called ''conservation'' (or Eulerian) differential form, with vector notation: |
Thanks to these vector identities, the incompressible Euler equations with constant and uniform density and without external field can be put in the so-called ''conservation'' (or Eulerian) differential form, with vector notation: |
||
<math display="block">\left\{\begin{align} |
|||
:<math>\left\{\begin{align} |
|||
{\partial\mathbf{u} \over \partial t} + \nabla \cdot \left(\mathbf{u} \otimes \mathbf{u} + w\mathbf{I}\right) &= \mathbf{0} \\ |
{\partial\mathbf{u} \over \partial t} + \nabla \cdot \left(\mathbf{u} \otimes \mathbf{u} + w\mathbf{I}\right) &= \mathbf{0} \\ |
||
{\partial 0 \over \partial t} + \nabla \cdot \mathbf{u} &= 0, |
{\partial 0 \over \partial t} + \nabla \cdot \mathbf{u} &= 0, |
||
\end{align}\right.</math> |
\end{align}\right.</math> |
||
or with Einstein notation: |
or with Einstein notation: |
||
<math display="block">\left\{\begin{align} |
|||
:<math>\left\{\begin{align} |
|||
\partial_t u_j + \partial_i \left(u_i u_j + w \delta_{ij}\right) &= 0 \\ |
\partial_t u_j + \partial_i \left(u_i u_j + w \delta_{ij}\right) &= 0 \\ |
||
\partial_t 0 + \partial_j u_j &= 0, |
\partial_t 0 + \partial_j u_j &= 0, |
||
| Line 166: | Line 147: | ||
Then '''incompressible''' Euler equations with uniform density have conservation variables: |
Then '''incompressible''' Euler equations with uniform density have conservation variables: |
||
<math display="block"> |
|||
\mathbf y = \begin{pmatrix}\mathbf u \\ 0 \end{pmatrix}; \qquad |
|||
:<math> |
|||
|
\mathbf F= \begin{pmatrix}\mathbf u \otimes \mathbf u + w \mathbf I \\ \mathbf u \end{pmatrix}. |
||
</math> |
</math> |
||
Note that in the second component u is by itself a vector, with length N, so y has length N+1 and F has size N(N+1). In 3D for example y has length 4, I has size 3×3 and F has size 4×3, so the explicit forms are: |
Note that in the second component u is by itself a vector, with length N, so y has length N+1 and F has size N(N+1). In 3D for example y has length 4, I has size 3×3 and F has size 4×3, so the explicit forms are: |
||
<math display="block"> |
|||
:<math> |
|||
{\mathbf y}=\begin{pmatrix} u_1 \\ u_2 \\ u_3 \\0 \end{pmatrix}; \quad |
{\mathbf y}=\begin{pmatrix} u_1 \\ u_2 \\ u_3 \\0 \end{pmatrix}; \quad |
||
{\mathbf F}=\begin{pmatrix} |
{\mathbf F}=\begin{pmatrix} |
||
| Line 190: | Line 170: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Incompressible Euler equation(s) with constant and uniform density''' |
|title='''Incompressible Euler equation(s) with constant and uniform density'''<br/>(''conservation or Eulerian form'') |
||
|equation=<math> |
|equation=<math> |
||
\frac {\partial}{\partial t}\begin{pmatrix} \mathbf u \\ 0 \end{pmatrix} + \nabla \cdot \begin{pmatrix}\mathbf u \otimes \mathbf u + w \mathbf I \\ \mathbf u \end{pmatrix} = \begin{pmatrix}\mathbf g \\ 0\end{pmatrix} |
\frac {\partial}{\partial t}\begin{pmatrix} \mathbf u \\ 0 \end{pmatrix} + \nabla \cdot \begin{pmatrix}\mathbf u \otimes \mathbf u + w \mathbf I \\ \mathbf u \end{pmatrix} = \begin{pmatrix}\mathbf g \\ 0\end{pmatrix} |
||
| Line 208: | Line 188: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Incompressible Euler equations''' |
|title='''Incompressible Euler equations'''<br/>(''convective or Lagrangian form'') |
||
|equation=<math>\left\{ \begin{align} |
|equation=<math>\left\{ \begin{align} |
||
{D\rho \over Dt} &= 0\\ |
{D\rho \over Dt} &= 0\\ |
||
| Line 225: | Line 205: | ||
The first equation, which is the new one, is the incompressible [[continuity equation]]. In fact the general continuity equation would be: |
The first equation, which is the new one, is the incompressible [[continuity equation]]. In fact the general continuity equation would be: |
||
<math display="block">{\partial \rho \over\partial t} + \mathbf u \cdot \nabla \rho + \rho \nabla \cdot \mathbf u = 0</math> |
|||
:<math>{\partial \rho \over\partial t} + \mathbf u \cdot \nabla \rho + \rho \nabla \cdot \mathbf u = 0</math> |
|||
but here the last term is identically zero for the incompressibility constraint. |
but here the last term is identically zero for the incompressibility constraint. |
||
| Line 233: | Line 212: | ||
{{See also|conservation equation|}} |
{{See also|conservation equation|}} |
||
The incompressible Euler equations in the Froude limit are equivalent to a single conservation equation with conserved quantity and associated flux respectively: |
The incompressible Euler equations in the Froude limit are equivalent to a single conservation equation with conserved quantity and associated flux respectively: |
||
<math display="block"> |
|||
\mathbf y = \begin{pmatrix}\rho \\ \rho \mathbf u \\0\end{pmatrix}; \qquad {\mathbf F} = \begin{pmatrix}\rho \mathbf u \\ \rho \mathbf u \otimes \mathbf u + p \mathbf I\\\mathbf u\end{pmatrix}. |
|||
:<math> |
|||
{\mathbf y}=\begin{pmatrix}\rho \\ \rho \mathbf u \\0\end{pmatrix}; \qquad {\mathbf F}=\begin{pmatrix}\rho \mathbf u\\\rho \mathbf u \otimes \mathbf u + p \mathbf I\\\mathbf u\end{pmatrix}. |
|||
</math> |
</math> |
||
Here <math>\mathbf y</math> has length <math>N+2</math> and <math>\mathbf F</math> has size <math>(N+2)N</math>.{{efn|In 3D for example <math>\mathbf y</math> has length 5, <math>\mathbf I</math> has size 3×3 and <math>\mathbf F</math> has size 5×3, so the explicit forms are: |
Here <math>\mathbf y</math> has length <math>N+2</math> and <math>\mathbf F</math> has size <math>(N+2)N</math>.{{efn|In 3D for example <math>\mathbf y</math> has length 5, <math>\mathbf I</math> has size 3×3 and <math>\mathbf F</math> has size 5×3, so the explicit forms are: |
||
|
<math display="block"> |
||
{\mathbf y}=\begin{pmatrix}\rho \\ \rho u_1 \\ \rho u_2 \\ \rho u_3 \\0\end{pmatrix}; \quad |
{\mathbf y}=\begin{pmatrix}\rho \\ \rho u_1 \\ \rho u_2 \\ \rho u_3 \\0\end{pmatrix}; \quad |
||
{\mathbf F}=\begin{pmatrix}\rho u_1 & \rho u_2 & \rho u_3 \\ |
{\mathbf F}=\begin{pmatrix}\rho u_1 & \rho u_2 & \rho u_3 \\ |
||
| Line 247: | Line 225: | ||
\\ u_1 & u_2 & u_3 \end{pmatrix}. |
\\ u_1 & u_2 & u_3 \end{pmatrix}. |
||
</math> |
</math> |
||
}} |
|||
}} In general (not only in the Froude limit) Euler equations are expressible as: |
|||
In general (not only in the Froude limit) Euler equations are expressible as: |
|||
|
<math display="block"> |
||
\frac {\partial}{\partial t}\begin{pmatrix}\rho \\ \rho \mathbf u \\0\end{pmatrix}+ \nabla \cdot \begin{pmatrix}\rho \mathbf u\\\rho \mathbf u \otimes \mathbf u + p \mathbf I\\ \mathbf u\end{pmatrix} = \begin{pmatrix}0 \\ \rho \mathbf g \\ 0 \end{pmatrix} |
\frac {\partial}{\partial t}\begin{pmatrix}\rho \\ \rho \mathbf u \\0\end{pmatrix}+ \nabla \cdot \begin{pmatrix}\rho \mathbf u\\\rho \mathbf u \otimes \mathbf u + p \mathbf I\\ \mathbf u\end{pmatrix} = \begin{pmatrix}0 \\ \rho \mathbf g \\ 0 \end{pmatrix} |
||
</math> |
</math> |
||
| Line 255: | Line 233: | ||
===Conservation variables=== |
===Conservation variables=== |
||
The variables for the equations in conservation form are not yet optimised. In fact we could define: |
The variables for the equations in conservation form are not yet optimised. In fact we could define: |
||
<math display="block"> |
|||
:<math> |
|||
{\mathbf y}=\begin{pmatrix}\rho \\ \mathbf j \\0\end{pmatrix}; \qquad {\mathbf F}=\begin{pmatrix} \mathbf j \\ \frac {1} \rho \, \mathbf j \otimes \mathbf j+ p \mathbf I\\ \frac \mathbf j \rho \end{pmatrix}. |
{\mathbf y}=\begin{pmatrix}\rho \\ \mathbf j \\0\end{pmatrix}; \qquad {\mathbf F}=\begin{pmatrix} \mathbf j \\ \frac {1} \rho \, \mathbf j \otimes \mathbf j+ p \mathbf I\\ \frac \mathbf j \rho \end{pmatrix}. |
||
</math> |
</math> |
||
where <math>\mathbf j = \rho \mathbf u</math> is the [[momentum]] density, a conservation variable. |
|||
where: |
|||
* <math>\mathbf j = \rho \mathbf u</math> is the [[momentum]] density, a conservation variable. |
|||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Incompressible Euler equation(s)''' |
|title='''Incompressible Euler equation(s)'''<br/>(''conservation or Eulerian form'') |
||
|equation=<math> |
|equation=<math> |
||
\frac {\partial}{\partial t}\begin{pmatrix}\rho \\ \mathbf j \\0\end{pmatrix}+ \nabla \cdot \begin{pmatrix}\mathbf j \\ \frac 1 \rho \, \mathbf j \otimes \mathbf j + p \mathbf I\\ \frac \mathbf j \rho\end{pmatrix} = \begin{pmatrix}0 \\ \mathbf f \\ 0 \end{pmatrix} |
\frac {\partial}{\partial t}\begin{pmatrix}\rho \\ \mathbf j \\0\end{pmatrix}+ \nabla \cdot \begin{pmatrix}\mathbf j \\ \frac 1 \rho \, \mathbf j \otimes \mathbf j + p \mathbf I\\ \frac \mathbf j \rho\end{pmatrix} = \begin{pmatrix}0 \\ \mathbf f \\ 0 \end{pmatrix} |
||
| Line 275: | Line 250: | ||
}} |
}} |
||
where <math>\mathbf f = \rho \mathbf g</math> is the [[force density]], a conservation variable. |
|||
where: |
|||
* <math>\mathbf f = \rho \mathbf g</math> is the [[force density]], a conservation variable. |
|||
==Euler equations== |
==Euler equations== |
||
| Line 283: | Line 257: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Euler equations''' |
|title='''Euler equations'''<br/>(''convective form'') |
||
|equation=<math>\left\{\begin{align} |
|equation=<math>\left\{\begin{align} |
||
{D\rho \over Dt} &= -\rho\nabla \cdot \mathbf{u} \\[1.2ex] |
{D\rho \over Dt} &= -\rho\nabla \cdot \mathbf{u} \\[1.2ex] |
||
| Line 302: | Line 276: | ||
If one expands the material derivative the equations above are: |
If one expands the material derivative the equations above are: |
||
<math display="block">\left\{\begin{align} |
|||
:<math>\left\{\begin{align} |
|||
{\partial\rho \over \partial t} + \mathbf{u} \cdot \nabla\rho + \rho\nabla \cdot \mathbf{u} &= 0 \\[1.2ex] |
{\partial\rho \over \partial t} + \mathbf{u} \cdot \nabla\rho + \rho\nabla \cdot \mathbf{u} &= 0 \\[1.2ex] |
||
\frac{\partial\mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla\mathbf{u} + \frac{\nabla p}{\rho} &= \mathbf{g} \\[1.2ex] |
\frac{\partial\mathbf{u}}{\partial t} + \mathbf{u} \cdot \nabla\mathbf{u} + \frac{\nabla p}{\rho} &= \mathbf{g} \\[1.2ex] |
||
| Line 311: | Line 284: | ||
===Incompressible constraint (revisited)=== |
===Incompressible constraint (revisited)=== |
||
Coming back to the incompressible case, it now becomes apparent that the ''incompressible constraint'' typical of the former cases actually is a particular form valid for incompressible flows of the ''energy equation'', and not of the mass equation. In particular, the incompressible constraint corresponds to the following very simple energy equation: |
Coming back to the incompressible case, it now becomes apparent that the ''incompressible constraint'' typical of the former cases actually is a particular form valid for incompressible flows of the ''energy equation'', and not of the mass equation. In particular, the incompressible constraint corresponds to the following very simple energy equation: |
||
<math display="block">\frac{D e}{D t} = 0 </math> |
|||
:<math>{D e \over D t} = 0 </math> |
|||
Thus '''for an incompressible inviscid fluid the specific internal energy is constant along the flow lines''', also in a time-dependent flow. The pressure in an incompressible flow acts like a [[Lagrange multiplier]], being the multiplier of the incompressible constraint in the energy equation, and consequently in incompressible flows it has no thermodynamic meaning. In fact, thermodynamics is typical of compressible flows and degenerates in incompressible flows.{{sfn|Quartapelle|Auteri|2013|p=13|loc=Ch. 9}} |
Thus '''for an incompressible inviscid fluid the specific internal energy is constant along the flow lines''', also in a time-dependent flow. The pressure in an incompressible flow acts like a [[Lagrange multiplier]], being the multiplier of the incompressible constraint in the energy equation, and consequently in incompressible flows it has no thermodynamic meaning. In fact, thermodynamics is typical of compressible flows and degenerates in incompressible flows.{{sfn|Quartapelle|Auteri|2013|p=13|loc=Ch. 9}} |
||
Basing on the mass conservation equation, one can put this equation in the conservation form: |
Basing on the mass conservation equation, one can put this equation in the conservation form: |
||
<math display="block">{\partial \rho e \over \partial t} + \nabla \cdot (\rho e \mathbf u) = 0 </math> |
|||
:<math>{\partial \rho e \over \partial t} + \nabla \cdot (\rho e \mathbf u) = 0 </math> |
|||
meaning that for an incompressible inviscid nonconductive flow a continuity equation holds for the internal energy. |
meaning that for an incompressible inviscid nonconductive flow a continuity equation holds for the internal energy. |
||
===Enthalpy conservation=== |
===Enthalpy conservation=== |
||
Since by definition the specific enthalpy is: |
Since by definition the specific enthalpy is: |
||
<math display="block">h = e + \frac p \rho </math> |
|||
:<math>h = e + \frac p \rho </math> |
|||
The material derivative of the specific internal energy can be expressed as: |
The material derivative of the specific internal energy can be expressed as: |
||
<math display="block">{D e \over Dt} = {D h \over Dt} - \frac 1 \rho \left({D p \over Dt} - \frac p \rho {D \rho \over Dt} \right)</math> |
|||
:<math>{D e \over Dt} = {D h \over Dt} - \frac 1 \rho \left({D p \over Dt} - \frac p \rho {D \rho \over Dt} \right)</math> |
|||
Then by substituting the momentum equation in this expression, one obtains: |
Then by substituting the momentum equation in this expression, one obtains: |
||
<math display="block">{D e \over Dt}= {D h \over Dt} - \frac 1 \rho \left(p \nabla \cdot \mathbf u + {D p \over Dt} \right)</math> |
|||
:<math>{D e \over Dt}= {D h \over Dt} - \frac 1 \rho \left(p \nabla \cdot \mathbf u + {D p \over Dt} \right)</math> |
|||
And by substituting the latter in the energy equation, one obtains that the enthalpy expression for the Euler energy equation: |
And by substituting the latter in the energy equation, one obtains that the enthalpy expression for the Euler energy equation: |
||
<math display="block">{D h \over Dt} = \frac 1 \rho {D p \over Dt} </math> |
|||
:<math>{D h \over Dt} = \frac 1 \rho {D p \over Dt} </math> |
|||
'''In a reference frame moving with an inviscid and nonconductive flow, the variation of enthalpy directly corresponds to a variation of pressure.''' |
'''In a reference frame moving with an inviscid and nonconductive flow, the variation of enthalpy directly corresponds to a variation of pressure.''' |
||
| Line 347: | Line 313: | ||
|Deduction of the form valid for thermodynamic systems |
|Deduction of the form valid for thermodynamic systems |
||
|Considering the first equation, variable must be changed from density to specific volume. By definition: |
|Considering the first equation, variable must be changed from density to specific volume. By definition: |
||
<math display="block"> v \equiv \frac 1 \rho </math> |
|||
:<math> v \equiv \frac 1 \rho </math> |
|||
Thus the following identities hold: |
Thus the following identities hold: |
||
<math display="block"> \nabla \rho = \nabla \left(\frac{1}{v}\right) = -\frac{1}{v^2} \nabla v</math> |
|||
|
<math display="block"> \frac{\partial\rho}{\partial t} = \frac{\partial}{\partial t} \left(\frac{1}{v}\right) = -\frac{1}{v^2} \frac{\partialv}{\partial t} </math> |
||
:<math> \frac{\partial\rho}{\partial t} = \frac{\partial}{\partial t} \left(\frac{1}{v}\right) = -\frac{1}{v^2} \frac{\partial v}{\partial t} </math> |
|||
Then by substituting these expressions in the mass conservation equation: |
Then by substituting these expressions in the mass conservation equation: |
||
<math display="block"> - \frac{\mathbf{u}}{v^2} \cdot \nabla v - \frac 1 {v^2} \frac {\partial v}{\partial t} = - \frac 1 v \nabla \cdot \mathbf{u} </math> |
|||
:<math> - \frac{\mathbf{u}}{v^2} \cdot \nabla v - \frac 1 {v^2} \frac {\partial v}{\partial t} = - \frac 1 v \nabla \cdot \mathbf{u} </math> |
|||
And by multiplication: |
And by multiplication: |
||
<math display="block"> {\partial v \over\partial t}+\mathbf u \cdot \nabla v = v \nabla \cdot \mathbf u </math> |
|||
:<math> {\partial v \over\partial t}+\mathbf u \cdot \nabla v = v \nabla \cdot \mathbf u </math> |
|||
This equation is the only belonging to general continuum equations, so only this equation have the same form for example also in Navier-Stokes equations. |
This equation is the only belonging to general continuum equations, so only this equation have the same form for example also in Navier-Stokes equations. |
||
On the other hand, the pressure in thermodynamics is the opposite of the partial derivative of the specific internal energy with respect to the specific volume: |
On the other hand, the pressure in thermodynamics is the opposite of the partial derivative of the specific internal energy with respect to the specific volume: |
||
<math display="block">p(v, s) = - {\partial e(v, s) \over \partial v}</math> |
|||
:<math>p(v, s) = - {\partial e(v, s) \over \partial v}</math> |
|||
since the internal energy in thermodynamics is a function of the two variables aforementioned, the pressure gradient contained into the momentum equation should be explicited as: |
since the internal energy in thermodynamics is a function of the two variables aforementioned, the pressure gradient contained into the momentum equation should be explicited as: |
||
<math display="block">- \nabla p (v,s) = - \frac {\partial p}{\partial v} \nabla v - \frac {\partial p}{\partial s} \nabla s = \frac {\partial^2 e}{\partial v^2} \nabla v + \frac {\partial^2 e}{\partial v \partial s}\nabla s </math> |
|||
:<math>- \nabla p (v,s) = - \frac {\partial p}{\partial v} \nabla v - \frac {\partial p}{\partial s} \nabla s = \frac {\partial^2 e}{\partial v^2} \nabla v + \frac {\partial^2 e}{\partial v \partial s}\nabla s </math> |
|||
It is convenient for brevity to switch the notation for the second order derivatives: |
It is convenient for brevity to switch the notation for the second order derivatives: |
||
<math display="block"> - \nabla p (v,s) = e_{vv} \nabla v + e_{vs} \nabla s </math> |
|||
:<math> - \nabla p (v,s) = e_{vv} \nabla v + e_{vs} \nabla s </math> |
|||
Finally, the energy equation: |
Finally, the energy equation: |
||
<math display="block">{D e \over Dt} = - p v \nabla \cdot \mathbf u </math> |
|||
can be further simplified in convective form by changing variable from specific energy to the specific entropy: in fact the [[first law of thermodynamics]] in local form can be written: |
|||
:<math>{D e \over Dt} = - p v \nabla \cdot \mathbf u </math> |
|||
<math display="block">{D e \over Dt} = T {D s \over Dt} - p {D v \over Dt}</math> |
|||
can be furtherly simplified in convective form by changing variable from specific energy to the specific entropy: in fact the [[first law of thermodynamics]] in local form can be written: |
|||
:<math>{D e \over Dt} = T {D s \over Dt} - p {D v \over Dt}</math> |
|||
by substituting the material derivative of the internal energy, the energy equation becomes: |
by substituting the material derivative of the internal energy, the energy equation becomes: |
||
<math display="block">T {D s \over Dt} + \frac p {\rho^2} \left( {D \rho \over Dt} + \rho \nabla \cdot \mathbf u \right) = 0</math> |
|||
:<math>T {D s \over Dt} + \frac p {\rho^2} \left( {D \rho \over Dt} + \rho \nabla \cdot \mathbf u \right) = 0</math> |
|||
now the term between parenthesis is identically zero according to the conservation of mass, then the Euler energy equation becomes simply: |
now the term between parenthesis is identically zero according to the conservation of mass, then the Euler energy equation becomes simply: |
||
<math display="block">{D s \over Dt} = 0</math> |
|||
:<math>{D s \over Dt} = 0</math> |
|||
|style = border: 1px solid lightgray; width: 90%; |
|style = border: 1px solid lightgray; width: 90%; |
||
| Line 401: | Line 352: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Euler equations''' |
|title='''Euler equations'''<br/>(''convective form, for a thermodynamic system'') |
||
|equation=<math>\left\{\begin{align} |
|equation=<math>\left\{\begin{align} |
||
{Dv \over Dt} &= v \nabla \cdot \mathbf u\\[1.2ex] |
{Dv \over Dt} &= v \nabla \cdot \mathbf u\\[1.2ex] |
||
| Line 419: | Line 370: | ||
In the general case and not only in the incompressible case, the energy equation means that '''for an inviscid thermodynamic fluid the specific entropy is constant along the [[flow lines]]''', also in a time-dependent flow. Basing on the mass conservation equation, one can put this equation in the conservation form:{{sfn|Landau|Lifshitz|2013|p=4|loc= Eqs 2.6 and 2.7}} |
In the general case and not only in the incompressible case, the energy equation means that '''for an inviscid thermodynamic fluid the specific entropy is constant along the [[flow lines]]''', also in a time-dependent flow. Basing on the mass conservation equation, one can put this equation in the conservation form:{{sfn|Landau|Lifshitz|2013|p=4|loc= Eqs 2.6 and 2.7}} |
||
<math display="block">{\partial \rho s \over \partial t} + \nabla \cdot (\rho s \mathbf u) = 0 </math> |
|||
:<math>{\partial \rho s \over \partial t} + \nabla \cdot (\rho s \mathbf u) = 0 </math> |
|||
meaning that for an inviscid nonconductive flow a continuity equation holds for the entropy. |
meaning that for an inviscid nonconductive flow a continuity equation holds for the entropy. |
||
On the other hand, the two second-order partial derivatives of the specific internal energy in the momentum equation require the specification of the [[fundamental equation of state]] of the material considered, i.e. of the specific internal energy as function of the two variables specific volume and specific entropy: |
On the other hand, the two second-order partial derivatives of the specific internal energy in the momentum equation require the specification of the [[fundamental equation of state]] of the material considered, i.e. of the specific internal energy as function of the two variables specific volume and specific entropy: |
||
<math display="block">e = e(v, s)</math> |
|||
:<math>e = e(v, s)</math> |
|||
The ''fundamental'' equation of state contains all the thermodynamic information about the system (Callen, 1985),{{sfn|Henderson|2000|p=152|loc=2.6 Thermodynamic properties of materials}} exactly like the couple of a ''thermal'' equation of state together with a ''caloric'' equation of state. |
The ''fundamental'' equation of state contains all the thermodynamic information about the system (Callen, 1985),{{sfn|Henderson|2000|p=152|loc=2.6 Thermodynamic properties of materials}} exactly like the couple of a ''thermal'' equation of state together with a ''caloric'' equation of state. |
||
| Line 433: | Line 381: | ||
{{See also|Conservation equation|}} |
{{See also|Conservation equation|}} |
||
The Euler equations in the Froude limit are equivalent to a single conservation equation with conserved quantity and associated flux respectively: |
The Euler equations in the Froude limit are equivalent to a single conservation equation with conserved quantity and associated flux respectively: |
||
<math display="block">\mathbf y = \begin{pmatrix} |
|||
:<math>{\mathbf y} = \begin{pmatrix} |
|||
\rho \\ |
\rho \\ |
||
\mathbf j \\ |
\mathbf j \\ |
||
| Line 450: | Line 397: | ||
Here <math>\mathbf y</math> has length N + 2 and <math>\mathbf F</math> has size N(N + 2).{{efn|In 3D for example y has length 5, I has size 3×3 and F has size 3×5, so the explicit forms are: |
Here <math>\mathbf y</math> has length N + 2 and <math>\mathbf F</math> has size N(N + 2).{{efn|In 3D for example y has length 5, I has size 3×3 and F has size 3×5, so the explicit forms are: |
||
|
<math display="block"> |
||
{\mathbf y} = \begin{pmatrix} j_1 \\ j_2 \\ j_3 \end{pmatrix}; \quad |
{\mathbf y} = \begin{pmatrix} j_1 \\ j_2 \\ j_3 \end{pmatrix}; \quad |
||
{\mathbf F} = \begin{pmatrix} |
{\mathbf F} = \begin{pmatrix} |
||
| Line 466: | Line 413: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Euler equation(s)''' |
|title='''Euler equation(s)'''<br/>(''original conservation or Eulerian form'') |
||
|equation=<math>\frac{\partial}{\partial t}\begin{pmatrix} |
|equation=<math>\frac{\partial}{\partial t}\begin{pmatrix} |
||
\rho \\ |
\rho \\ |
||
| Line 487: | Line 434: | ||
}} |
}} |
||
where <math>\mathbf f = \rho \mathbf g</math> is the [[force density]], a conservation variable. |
|||
where: |
|||
* <math>\mathbf f = \rho \mathbf g</math> is the [[force density]], a conservation variable. |
|||
We remark that also the Euler equation even when conservative (no external field, Froude limit) have '''no [[Riemann invariant]]s''' in general.{{sfn|Chorin|Marsden|2013|p=118|loc=par. 3.2 Shocks}} Some further assumptions are required |
We remark that also the Euler equation even when conservative (no external field, Froude limit) have '''no [[Riemann invariant]]s''' in general.{{sfn|Chorin|Marsden|2013|p=118|loc=par. 3.2 Shocks}} Some further assumptions are required |
||
However, we already mentioned that for a thermodynamic fluid the equation for the total energy density is equivalent to the conservation equation: |
However, we already mentioned that for a thermodynamic fluid the equation for the total energy density is equivalent to the conservation equation: |
||
<math display="block">{\partial \over \partial t} (\rho s) + \nabla \cdot (\rho s \mathbf u) = 0 </math> |
|||
:<math>{\partial \over \partial t} (\rho s) + \nabla \cdot (\rho s \mathbf u) = 0 </math> |
|||
Then the conservation equations in the case of a thermodynamic fluid are more simply expressed as: |
Then the conservation equations in the case of a thermodynamic fluid are more simply expressed as: |
||
| Line 500: | Line 445: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Euler equation(s)''' |
|title='''Euler equation(s)'''<br/>(''conservation form, for thermodynamic fluids'') |
||
|equation=<math> |
|equation=<math> |
||
\frac{\partial}{\partial t}\begin{pmatrix}\rho \\ \mathbf{j} \\S \end{pmatrix} + \nabla \cdot \begin{pmatrix}\mathbf{j} \\ \frac{1}{\rho}\mathbf{j} \otimes \mathbf{j} + p\mathbf{I} \\ S\frac{\mathbf{j}}{\rho}\end{pmatrix} = |
\frac{\partial}{\partial t}\begin{pmatrix}\rho \\ \mathbf{j} \\S \end{pmatrix} + \nabla \cdot \begin{pmatrix}\mathbf{j} \\ \frac{1}{\rho}\mathbf{j} \otimes \mathbf{j} + p\mathbf{I} \\ S\frac{\mathbf{j}}{\rho}\end{pmatrix} = |
||
| Line 511: | Line 456: | ||
}} |
}} |
||
where <math>S = \rho s</math> is the entropy density, a thermodynamic conservation variable. |
|||
where: |
|||
* <math>S = \rho s</math> is the entropy density, a thermodynamic conservation variable. |
|||
Another possible form for the energy equation, being particularly useful for [[isobaric process|isobarics]], is: |
Another possible form for the energy equation, being particularly useful for [[isobaric process|isobarics]], is: |
||
<math display="block"> |
|||
:<math> |
|||
\frac{\partial H^t}{\partial t} + \nabla \cdot \left(H^t \mathbf u\right) = |
\frac{\partial H^t}{\partial t} + \nabla \cdot \left(H^t \mathbf u\right) = |
||
\mathbf u \cdot \mathbf f - \frac{\partial p}{\partial t} |
\mathbf u \cdot \mathbf f - \frac{\partial p}{\partial t} |
||
</math> |
</math> |
||
where <math display="inline">H^t = E^t + p = \rho e + p + \frac{1}{2} \rho u^2</math> is the total [[enthalpy]] density. |
|||
where: |
|||
*<math display="inline">H^t = E^t + p = \rho e + p + \frac{1}{2} \rho u^2</math> is the total [[enthalpy]] density. |
|||
==Quasilinear form and characteristic equations== |
==Quasilinear form and characteristic equations== |
||
Expanding the [[flux]]es can be an important part of constructing [[numerical solution|numerical solvers]], for example by exploiting ([[approximation|approximate]]) solutions to the [[Riemann problem]]. In regions where the state vector '''''y''''' varies smoothly, the equations in conservative form can be put in quasilinear form |
Expanding the [[flux]]es can be an important part of constructing [[numerical solution|numerical solvers]], for example by exploiting ([[approximation|approximate]]) solutions to the [[Riemann problem]]. In regions where the state vector '''''y''''' varies smoothly, the equations in conservative form can be put in quasilinear form: |
||
<math display="block"> \frac{\partial \mathbf y}{\partial t} + \mathbf A_i \frac{\partial \mathbf y}{\partial r_i} = {\mathbf 0}. </math> |
|||
:<math> \frac{\partial \mathbf y}{\partial t} + \mathbf A_i \frac{\partial \mathbf y}{\partial r_i} = {\mathbf 0}. </math> |
|||
where <math>\mathbf A_i</math> are called the flux [[Jacobian matrix and determinant|Jacobian]]s defined as the [[matrix (mathematics)|matrices]]: |
where <math>\mathbf A_i</math> are called the flux [[Jacobian matrix and determinant|Jacobian]]s defined as the [[matrix (mathematics)|matrices]]: |
||
<math display="block"> \mathbf A_i (\mathbf y)=\frac{\partial \mathbf f_i (\mathbf y)}{\partial \mathbf y}. </math> |
|||
:<math> \mathbf A_i (\mathbf y)=\frac{\partial \mathbf f_i (\mathbf y)}{\partial \mathbf y}. </math> |
|||
Obviously this Jacobian does not exist in discontinuity regions (e.g. contact discontinuities, shock waves in inviscid nonconductive flows). If the flux Jacobians <math>\mathbf A_i</math> are not functions of the state vector <math>\mathbf y</math>, the equations reveals ''linear''. |
Obviously this Jacobian does not exist in discontinuity regions (e.g. contact discontinuities, shock waves in inviscid nonconductive flows). If the flux Jacobians <math>\mathbf A_i</math> are not functions of the state vector <math>\mathbf y</math>, the equations reveals ''linear''. |
||
| Line 541: | Line 479: | ||
If <math>\mathbf p_i</math> is the [[right eigenvector]] of the matrix <math>\mathbf A</math> corresponding to the [[eigenvalue]] <math>\lambda_i</math>, by building the [[projection matrix]]: |
If <math>\mathbf p_i</math> is the [[right eigenvector]] of the matrix <math>\mathbf A</math> corresponding to the [[eigenvalue]] <math>\lambda_i</math>, by building the [[projection matrix]]: |
||
<math display="block">\mathbf{P} = \left[\mathbf{p}_1, \mathbf{p}_2, ..., \mathbf{p}_n\right]</math> |
|||
:<math>\mathbf{P} = \left[\mathbf{p}_1, \mathbf{p}_2, ..., \mathbf{p}_n\right]</math> |
|||
One can finally find the ''characteristic variables'' as: |
One can finally find the ''characteristic variables'' as: |
||
<math display="block">\mathbf{w} = \mathbf{P}^{-1} \mathbf{y},</math> |
|||
:<math>\mathbf{w}= \mathbf{P}^{-1}\mathbf{y},</math> |
|||
Since '''A''' is constant, multiplying the original 1-D equation in flux-Jacobian form with '''P'''<sup>−1</sup> yields the characteristic equations:{{sfn|Toro|1999|p= 52|loc= par 2.3 Linear Hyperbolic System}} |
Since '''A''' is constant, multiplying the original 1-D equation in flux-Jacobian form with '''P'''<sup>−1</sup> yields the characteristic equations:{{sfn|Toro|1999|p= 52|loc= par 2.3 Linear Hyperbolic System}} |
||
<math display="block"> |
|||
:<math> |
|||
\frac{\partial w_i}{\partial t} + \lambda_j \frac{\partial w_i}{\partial r_j} = 0_i |
\frac{\partial w_i}{\partial t} + \lambda_j \frac{\partial w_i}{\partial r_j} = 0_i |
||
</math> |
</math> |
||
The original equations have been [[Linear independence|decoupled]] into N+2 characteristic equations each describing a simple wave, with the eigenvalues being the wave speeds. The variables ''w''<sub>i</sub> are called the ''characteristic variables'' and are a subset of the conservative variables. The solution of the initial value problem in terms of characteristic variables is finally very simple. In one spatial dimension it is: |
The original equations have been [[Linear independence|decoupled]] into N+2 characteristic equations each describing a simple wave, with the eigenvalues being the wave speeds. The variables ''w''<sub>''i''</sub> are called the ''characteristic variables'' and are a subset of the conservative variables. The solution of the initial value problem in terms of characteristic variables is finally very simple. In one spatial dimension it is: |
||
<math display="block">w_i(x, t) = w_i\left(x - \lambda_i t, 0\right)</math> |
|||
:<math>w_i(x, t) = w_i\left(x - \lambda_i t, 0\right)</math> |
|||
Then the solution in terms of the original conservative variables is obtained by transforming back: |
Then the solution in terms of the original conservative variables is obtained by transforming back: |
||
<math display="block">\mathbf{y} = \mathbf{P} \mathbf{w},</math> |
|||
:<math>\mathbf{y} = \mathbf{P} \mathbf{w},</math> |
|||
this computation can be explicited as the linear combination of the eigenvectors: |
this computation can be explicited as the linear combination of the eigenvectors: |
||
<math display="block">\mathbf{y}(x, t) = \sum_{i=1}^m w_i\left(x - \lambda_i t, 0\right) \mathbf p_i,</math> |
|||
:<math>\mathbf{y}(x, t) = \sum_{i=1}^m w_i\left(x - \lambda_i t, 0\right) \mathbf p_i,</math> |
|||
Now it becomes apparent that the characteristic variables act as weights in the linear combination of the jacobian eigenvectors. The solution can be seen as superposition of waves, each of which is advected independently without change in shape. Each ''i''-th wave has shape ''w''<sub>''i''</sub>''p''<sub>''i''</sub> and speed of propagation ''λ''<sub>''i''</sub>. In the following we show a very simple example of this solution procedure. |
Now it becomes apparent that the characteristic variables act as weights in the linear combination of the jacobian eigenvectors. The solution can be seen as superposition of waves, each of which is advected independently without change in shape. Each ''i''-th wave has shape ''w''<sub>''i''</sub>''p''<sub>''i''</sub> and speed of propagation ''λ''<sub>''i''</sub>. In the following we show a very simple example of this solution procedure. |
||
===Waves in 1D inviscid, nonconductive thermodynamic fluid=== |
===Waves in 1D inviscid, nonconductive thermodynamic fluid=== |
||
If one considers Euler equations for a thermodynamic fluid with the two further assumptions of one spatial dimension and free (no external field: ''g'' = 0) |
If one considers Euler equations for a thermodynamic fluid with the two further assumptions of one spatial dimension and free (no external field: ''g'' = 0): |
||
<math display="block">\left\{\begin{align} |
|||
:<math>\left\{\begin{align} |
|||
{\partial v \over \partial t} + u{\partial v \over \partial x} - v {\partial u \over \partial x} &= 0 \\[1.2ex] |
{\partial v \over \partial t} + u{\partial v \over \partial x} - v {\partial u \over \partial x} &= 0 \\[1.2ex] |
||
{\partial u \over \partial t} + u{\partial u \over \partial x} - e_{vv} v {\partial v \over \partial x} - e_{vs}v {\partial s \over \partial x} &= 0 \\[1.2ex] |
{\partial u \over \partial t} + u{\partial u \over \partial x} - e_{vv} v {\partial v \over \partial x} - e_{vs}v {\partial s \over \partial x} &= 0 \\[1.2ex] |
||
| Line 578: | Line 508: | ||
If one defines the vector of variables: |
If one defines the vector of variables: |
||
<math display="block">\mathbf{y} = \begin{pmatrix}v \\ u \\ s\end{pmatrix}</math> |
|||
:<math>\mathbf{y} = \begin{pmatrix}v \\ u \\ s\end{pmatrix}</math> |
|||
recalling that <math>v</math> is the specific volume, <math>u</math> the flow speed, <math>s</math> the specific entropy, the corresponding jacobian matrix is: |
recalling that <math>v</math> is the specific volume, <math>u</math> the flow speed, <math>s</math> the specific entropy, the corresponding jacobian matrix is: |
||
<math display="block">{\mathbf A}=\begin{pmatrix}u & -v & 0 \\ - e_{vv} v & u & - e_{vs} v \\ 0 & 0 & u \end{pmatrix}.</math> |
|||
: <math>{\mathbf A}=\begin{pmatrix}u & -v & 0 \\ - e_{vv} v & u & - e_{vs} v \\ 0 & 0 & u \end{pmatrix}.</math> |
|||
At first one must find the eigenvalues of this matrix by solving the [[characteristic equation (calculus)|characteristic equation]]: |
At first one must find the eigenvalues of this matrix by solving the [[characteristic equation (calculus)|characteristic equation]]: |
||
<math display="block">\det(\mathbf A(\mathbf y) - \lambda(\mathbf y) \mathbf I) = 0</math> |
|||
: <math>\det(\mathbf A(\mathbf y) - \lambda(\mathbf y) \mathbf I) = 0</math> |
|||
that is explicitly: |
that is explicitly: |
||
<math display="block">\det\begin{bmatrix}u-\lambda & -v & 0 \\ - e_{vv} v & u-\lambda & - e_{vs} v \\ 0 & 0 & u-\lambda \end{bmatrix}=0</math> |
|||
: <math>\det\begin{bmatrix}u-\lambda & -v & 0 \\ - e_{vv} v & u-\lambda & - e_{vs} v \\ 0 & 0 & u-\lambda \end{bmatrix}=0</math> |
|||
This [[determinant]] is very simple: the fastest computation starts on the last row, since it has the highest number of zero elements. |
This [[determinant]] is very simple: the fastest computation starts on the last row, since it has the highest number of zero elements. |
||
<math display="block">(u-\lambda) \det \begin{bmatrix}u-\lambda & -v \\ - e_{vv} v & u -\lambda \end{bmatrix}=0</math> |
|||
: <math>(u-\lambda) \det \begin{bmatrix}u-\lambda & -v \\ - e_{vv} v & u -\lambda \end{bmatrix}=0</math> |
|||
Now by computing the determinant 2×2: |
Now by computing the determinant 2×2: |
||
<math display="block">(u - \lambda)\left((u - \lambda)^2 - e_{vv} v^2\right) = 0</math> |
|||
: <math>(u - \lambda)\left((u - \lambda)^2 - e_{vv} v^2\right) = 0</math> |
|||
by defining the parameter: |
by defining the parameter: |
||
<math display="block">a(v,s) \equiv v \sqrt {e_{vv}} </math> |
|||
: <math>a(v,s) \equiv v \sqrt {e_{vv}} </math> |
|||
or equivalently in mechanical variables, as: |
or equivalently in mechanical variables, as: |
||
<math display="block">a(\rho,p) \equiv \sqrt {\partial p \over \partial \rho} </math> |
|||
: <math>a(\rho,p) \equiv \sqrt {\partial p \over \partial \rho} </math> |
|||
This parameter is always real according to the [[second law of thermodynamics]]. In fact the second law of thermodynamics can be expressed by several postulates. The most elementary of them in mathematical terms is the statement of convexity of the fundamental equation of state, i.e. the [[hessian matrix]] of the specific energy expressed as function of specific volume and specific entropy: |
This parameter is always real according to the [[second law of thermodynamics]]. In fact the second law of thermodynamics can be expressed by several postulates. The most elementary of them in mathematical terms is the statement of convexity of the fundamental equation of state, i.e. the [[hessian matrix]] of the specific energy expressed as function of specific volume and specific entropy: |
||
<math display="block"> \begin{pmatrix}e_{vv} & e_{vs} \\ e_{vs} & e_{ss} \end{pmatrix}</math> |
|||
: <math> \begin{pmatrix}e_{vv} & e_{vs} \\ e_{vs} & e_{ss} \end{pmatrix}</math> |
|||
is defined positive. This statement corresponds to the two conditions: |
is defined positive. This statement corresponds to the two conditions: |
||
<math display="block">\left\{\begin{align} |
|||
:<math>\left\{\begin{align} |
|||
e_{vv} &> 0 \\[1.2ex] |
e_{vv} &> 0 \\[1.2ex] |
||
e_{vv}e_{ss} - e_{vs}^2 &> 0 |
e_{vv}e_{ss} - e_{vs}^2 &> 0 |
||
| Line 623: | Line 539: | ||
The characteristic equation finally results: |
The characteristic equation finally results: |
||
<math display="block">(u - \lambda)\left((u - \lambda)^2 - a^2\right) = 0</math> |
|||
: <math>(u - \lambda)\left((u - \lambda)^2 - a^2\right) = 0</math> |
|||
That has three real solutions: |
That has three real solutions: |
||
<math display="block">\lambda_1(v,u,s) = u-a(v,s) \quad \lambda_2(u)= u, \quad \lambda_3(v,u,s) = u+a(v,s)</math> |
|||
: <math>\lambda_1(v,u,s) = u-a(v,s) \quad \lambda_2(u)= u, \quad \lambda_3(v,u,s) = u+a(v,s)</math> |
|||
Then the matrix has three real eigenvalues all distinguished: the 1D Euler equations are a '''strictly hyperbolic system'''. |
Then the matrix has three real eigenvalues all distinguished: the 1D Euler equations are a '''strictly hyperbolic system'''. |
||
At this point one should determine the three eigenvectors: each one is obtained by substituting one eigenvalue in the eigenvalue equation and then solving it. By substituting the first eigenvalue λ<sub>1</sub> one obtains: |
At this point one should determine the three eigenvectors: each one is obtained by substituting one eigenvalue in the eigenvalue equation and then solving it. By substituting the first eigenvalue λ<sub>1</sub> one obtains: |
||
<math display="block">\begin{pmatrix}a & -v & 0 \\ - e_{vv} v & a & - e_{vs} v \\ 0 & 0 & a \end{pmatrix} \begin{pmatrix}v_1\\ u_1 \\s_1 \end{pmatrix}=0</math> |
|||
Basing on the third equation that simply has solution ''s''<sub>1</sub>=0, the system reduces to: |
|||
: <math>\begin{pmatrix}a & -v & 0 \\ - e_{vv} v & a & - e_{vs} v \\ 0 & 0 & a \end{pmatrix} \begin{pmatrix}v_1\\ u_1 \\s_1 \end{pmatrix}=0</math> |
|||
<math display="block">\begin{pmatrix}a & -v \\-a^2 /v& a \end{pmatrix} \begin{pmatrix}v_1\\ u_1 \end{pmatrix}=0</math> |
|||
Basing on the third equation that simply has solution s<sub>1</sub>=0, the system reduces to: |
|||
: <math>\begin{pmatrix}a & -v \\-a^2 /v& a \end{pmatrix} \begin{pmatrix}v_1\\ u_1 \end{pmatrix}=0</math> |
|||
The two equations are redundant as usual, then the eigenvector is defined with a multiplying constant. We choose as right eigenvector: |
The two equations are redundant as usual, then the eigenvector is defined with a multiplying constant. We choose as right eigenvector: |
||
<math display="block"> \mathbf p_1=\begin{pmatrix}v\\ a \\0\end{pmatrix}</math> |
|||
: <math> \mathbf p_1=\begin{pmatrix}v\\ a \\0\end{pmatrix}</math> |
|||
The other two eigenvectors can be found with analogous procedure as: |
The other two eigenvectors can be found with analogous procedure as: |
||
<math display="block"> \mathbf p_2=\begin{pmatrix} e_{vs} \\ 0\\ - \left(\frac a v \right)^2 \end{pmatrix}, \qquad \mathbf p_3 = \begin{pmatrix}v\\ -a \\0\end{pmatrix}</math> |
|||
: <math> \mathbf p_2=\begin{pmatrix} e_{vs} \\ 0\\ - \left(\frac a v \right)^2 \end{pmatrix}, \qquad \mathbf p_3=\begin{pmatrix}v\\ -a \\0\end{pmatrix}</math> |
|||
Then the projection matrix can be built: |
Then the projection matrix can be built: |
||
<math display="block"> \mathbf P (v,u,s)=( \mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_3) =\begin{pmatrix} v & e_{vs} & v\\ a & 0 & -a \\ 0 & - \left(\frac a v \right)^2 & 0 \end{pmatrix}</math> |
|||
: <math> \mathbf P (v,u,s)=( \mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_3) =\begin{pmatrix} v & e_{vs} & v\\ a & 0 & -a \\ 0 & - \left(\frac a v \right)^2 & 0 \end{pmatrix}</math> |
|||
Finally it becomes apparent that the real parameter ''a'' previously defined is the speed of propagation of the information characteristic of the hyperbolic system made of Euler equations, i.e. it is the ''[[group velocity|wave speed]]''. It remains to be shown that the sound speed corresponds to the particular case of an [[Isentropic process|isentropic transformation]]: |
Finally it becomes apparent that the real parameter ''a'' previously defined is the speed of propagation of the information characteristic of the hyperbolic system made of Euler equations, i.e. it is the ''[[group velocity|wave speed]]''. It remains to be shown that the sound speed corresponds to the particular case of an [[Isentropic process|isentropic transformation]]: |
||
<math display="block">a_s \equiv \sqrt {\left({\partial p \over \partial \rho} \right)_s} </math> |
|||
:<math>a_s \equiv \sqrt {\left({\partial p \over \partial \rho} \right)_s} </math> |
|||
===Compressibility and sound speed=== |
===Compressibility and sound speed=== |
||
Sound speed is defined as the wavespeed of an isentropic transformation: |
Sound speed is defined as the wavespeed of an isentropic transformation: |
||
<math display="block">a_s(\rho,p) \equiv \sqrt {\left({\partial p \over \partial \rho} \right)_s} </math> |
|||
:<math>a_s(\rho,p) \equiv \sqrt {\left({\partial p \over \partial \rho} \right)_s} </math> |
|||
by the definition of the isoentropic compressibility: |
by the definition of the isoentropic compressibility: |
||
<math display="block">K_s (\rho,p) \equiv \rho \left({\partial p \over \partial \rho} \right)_s </math> |
|||
:<math>K_s (\rho,p) \equiv \frac 1 \rho \left({\partial p \over \partial \rho} \right)_s </math> |
|||
the soundspeed results always the square root of ratio between the isentropic compressibility and the density: |
the soundspeed results always the square root of ratio between the isentropic compressibility and the density: |
||
<math display="block">a_s \equiv \sqrt {\frac {K_s} \rho} </math> |
|||
:<math>a_s \equiv \sqrt {\frac {K_s} \rho} </math> |
|||
====Ideal gas==== |
====Ideal gas==== |
||
The sound speed in an ideal gas depends only on its temperature: |
The sound speed in an ideal gas depends only on its temperature: |
||
<math display="block">a_s (T) = \sqrt {\gamma \frac T m} </math> |
|||
:<math>a_s (T) = \sqrt {\gamma \frac T m} </math> |
|||
{{hidden |
{{hidden |
||
|Deduction of the form valid for ideal gases |
|Deduction of the form valid for ideal gases |
||
|In an ideal gas the isoentropic transformation is described by the [[Poisson's law]]: |
|In an ideal gas the isoentropic transformation is described by the [[Poisson's law]]: |
||
<math display="block">d\left(p\rho^{-\gamma}\right)_s = 0</math> |
|||
:<math>d\left(p\rho^{-\gamma}\right)_s = 0</math> |
|||
where ''γ'' is the [[heat capacity ratio]], a constant for the material. By explicitating the differentials: |
where ''γ'' is the [[heat capacity ratio]], a constant for the material. By explicitating the differentials: |
||
|
<math display="block">\rho^{-\gamma} (d p)_s + \gamma p \rho^{-\gamma-1} (d \rho)_s =0</math> |
||
and by dividing for ''ρ''<sup>−''γ''</sup> d''ρ'': |
and by dividing for ''ρ''<sup>−''γ''</sup> d''ρ'': |
||
|
<math display="block">\left({\partial p \over \partial \rho}\right)_s = \gamma p \rho</math> |
||
Then by substitution in the general definitions for an ideal gas the isentropic compressibility is simply proportional to the pressure: |
Then by substitution in the general definitions for an ideal gas the isentropic compressibility is simply proportional to the pressure: |
||
|
<math display="block">K_s (p) = \gamma p </math> |
||
and the sound speed results ('''Newton–Laplace law'''): |
and the sound speed results ('''Newton–Laplace law'''): |
||
|
<math display="block">a_s (\rho,p) = \sqrt {\gamma \frac p \rho} </math> |
||
Notably, for an ideal gas the [[ideal gas law]] holds, that in mathematical form is simply: |
Notably, for an ideal gas the [[ideal gas law]] holds, that in mathematical form is simply: |
||
|
<math display="block">p = n T </math> |
||
where ''n'' is the [[number density]], and ''T'' is the [[absolute temperature]], provided it is measured in ''energetic units'' (i.e. in [[joules]]) through multiplication with the [[Boltzmann constant]]. Since the mass density is proportional to the number density through the average [[molecular mass]] ''m'' of the material: |
where ''n'' is the [[number density]], and ''T'' is the [[absolute temperature]], provided it is measured in ''energetic units'' (i.e. in [[joules]]) through multiplication with the [[Boltzmann constant]]. Since the mass density is proportional to the number density through the average [[molecular mass]] ''m'' of the material: |
||
|
<math display="block"> \rho = m n </math> |
||
The ideal gas law can be recast into the formula: |
The ideal gas law can be recast into the formula: |
||
|
<math display="block"> \frac p \rho = \frac T m </math> |
||
By substituting this ratio in the Newton–Laplace law, the expression of the sound speed into an ideal gas as function of temperature is finally achieved. |
By substituting this ratio in the Newton–Laplace law, the expression of the sound speed into an ideal gas as function of temperature is finally achieved. |
||
| Line 716: | Line 616: | ||
Since the specific enthalpy in an ideal gas is proportional to its temperature: |
Since the specific enthalpy in an ideal gas is proportional to its temperature: |
||
|
<math display="block">h = c_p T = \frac {\gamma}{\gamma-1} \frac T m </math> |
||
the sound speed in an ideal gas can also be made dependent only on its specific enthalpy: |
the sound speed in an ideal gas can also be made dependent only on its specific enthalpy: |
||
|
<math display="block">a_s (h) = \sqrt {(\gamma -1) h} </math> |
||
==Bernoulli's theorem for steady inviscid flow== |
==Bernoulli's theorem for steady inviscid flow== |
||
| Line 728: | Line 628: | ||
The [[vector calculus identity]] of the [[Curl (mathematics)#Identities|cross product of a curl]] holds: |
The [[vector calculus identity]] of the [[Curl (mathematics)#Identities|cross product of a curl]] holds: |
||
|
<math display="block"> \mathbf{v \ \times } \left( \mathbf{ \nabla \times F} \right) = \nabla_F \left( \mathbf{v \cdot F } \right) - \mathbf{v \cdot \nabla } \mathbf{ F} \ , </math> |
||
where the Feynman subscript notation <math>\nabla_F</math> is used, which means the subscripted gradient operates only on the factor <math>\mathbf F</math>. |
where the Feynman subscript notation <math>\nabla_F</math> is used, which means the subscripted gradient operates only on the factor <math>\mathbf F</math>. |
||
| Line 734: | Line 634: | ||
[[Horace Lamb|Lamb]] in his famous classical book Hydrodynamics (1895), still in print, used this identity to change the convective term of the flow velocity in rotational form:{{sfn| Valorani| Nasuti|n.d.|pp= 11–12}} |
[[Horace Lamb|Lamb]] in his famous classical book Hydrodynamics (1895), still in print, used this identity to change the convective term of the flow velocity in rotational form:{{sfn| Valorani| Nasuti|n.d.|pp= 11–12}} |
||
|
<math display="block">\mathbf u \cdot \nabla \mathbf u = \frac{1}{2}\nabla\left(u^2\right) + (\nabla \times \mathbf u) \times \mathbf u</math> |
||
the Euler momentum equation in Lamb's form becomes: |
the Euler momentum equation in Lamb's form becomes: |
||
|
<math display="block"> |
||
\frac{\partial\mathbf{u}}{\partial t} + \frac{1}{2}\nabla\left(u^2\right) + (\nabla \times \mathbf{u}) \times \mathbf{u} + \frac{\nabla p}{\rho} = \mathbf{g} = |
\frac{\partial\mathbf{u}}{\partial t} + \frac{1}{2}\nabla\left(u^2\right) + (\nabla \times \mathbf{u}) \times \mathbf{u} + \frac{\nabla p}{\rho} = \mathbf{g} = |
||
\frac{\partial\mathbf{u}}{\partial t} + \frac{1}{2}\nabla\left(u^2\right) - \mathbf{u} \times (\nabla \times \mathbf{u}) + \frac{\nabla p}{\rho} |
\frac{\partial\mathbf{u}}{\partial t} + \frac{1}{2}\nabla\left(u^2\right) - \mathbf{u} \times (\nabla \times \mathbf{u}) + \frac{\nabla p}{\rho} |
||
| Line 747: | Line 647: | ||
Now, basing on the other identity: |
Now, basing on the other identity: |
||
|
<math display="block">\nabla \left( \frac {p}{\rho} \right) = \frac {\nabla p}{\rho} - \frac{p}{\rho^2} \nabla \rho </math> |
||
the Euler momentum equation assumes a form that is optimal to demonstrate [[Bernoulli's theorem]] for steady flows: |
the Euler momentum equation assumes a form that is optimal to demonstrate [[Bernoulli's theorem]] for steady flows: |
||
|
<math display="block">\nabla \left(\frac{1}{2}u^2 + \frac{p}{\rho}\right) - \mathbf g = -\frac{p}{\rho^2} \nabla \rho + \mathbf u \times (\nabla \times \mathbf u) - \frac{\partial \mathbf u}{\partial t} </math> |
||
In fact, in case of an external [[conservative field]], by defining its potential φ: |
In fact, in case of an external [[conservative field]], by defining its potential φ: |
||
|
<math display="block">\nabla \left( \frac 1 2 u^2 + \phi + \frac p \rho \right) = -\frac{p}{\rho^2} \nabla \rho + \mathbf u \times (\nabla \times \mathbf u) - \frac{\partial \mathbf u}{\partial t}</math> |
||
In case of a steady flow the time derivative of the flow velocity disappears, so the momentum equation becomes: |
In case of a steady flow the time derivative of the flow velocity disappears, so the momentum equation becomes: |
||
|
<math display="block">\nabla \left( \frac 1 2 u^2 + \phi + \frac p \rho \right) = -\frac{p}{\rho^2} \nabla \rho + \mathbf u \times (\nabla \times \mathbf u)</math> |
||
And by projecting the momentum equation on the flow direction, i.e. along a ''[[streamlines, streaklines and pathlines|streamline]]'', the cross product disappears because its result is always perpendicular to the velocity: |
And by projecting the momentum equation on the flow direction, i.e. along a ''[[streamlines, streaklines and pathlines|streamline]]'', the cross product disappears because its result is always perpendicular to the velocity: |
||
|
<math display="block">\mathbf u \cdot \nabla \left(\frac{1}{2}u^2 + \phi + \frac{p}{\rho}\right) = -\frac{p}{\rho^2} \mathbf u \cdot \nabla\rho</math> |
||
In the steady incompressible case the mass equation is simply: |
In the steady incompressible case the mass equation is simply: |
||
<math display="block">\mathbf u \cdot \nabla \rho = 0,</math>that is '''the mass conservation for a steady incompressible flow states that the density along a streamline is constant'''. Then the Euler momentum equation in the steady incompressible case becomes: |
|||
:<math>\mathbf u \cdot \nabla \rho = 0</math>, |
|||
<math display="block">\mathbf u \cdot \nabla \left( \frac 1 2 u^2 + \phi + \frac p \rho \right) = 0</math> |
|||
that is '''the mass conservation for a steady incompressible flow states that the density along a streamline is constant'''. Then the Euler momentum equation in the steady incompressible case becomes: |
|||
:<math>\mathbf u \cdot \nabla \left( \frac 1 2 u^2 + \phi + \frac p \rho \right) = 0</math> |
|||
The convenience of defining the [[total head]] for an inviscid liquid flow is now apparent: |
The convenience of defining the [[total head]] for an inviscid liquid flow is now apparent: |
||
|
<math display="block"> b_l \equiv \frac 1 2 u^2 + \phi + \frac p \rho , </math> |
||
which may be simply written as: |
which may be simply written as: |
||
|
<math display="block">\mathbf u \cdot \nabla b_l = 0</math> |
||
That is, '''the momentum balance for a steady inviscid and incompressible flow in an external conservative field states that the total head along a streamline is constant'''. |
That is, '''the momentum balance for a steady inviscid and incompressible flow in an external conservative field states that the total head along a streamline is constant'''. |
||
===Compressible case === |
===Compressible case === |
||
In the most general steady ( |
In the most general steady (compressible) case the mass equation in conservation form is: |
||
:<math> \nabla \cdot \mathbf j = \rho \nabla \cdot \mathbf u + \mathbf u \cdot \nabla \rho = 0</math> . |
|||
Therefore, the previous expression is rather |
<math display="block"> \nabla \cdot \mathbf j = \rho \nabla \cdot \mathbf u + \mathbf u \cdot \nabla \rho = 0.</math>Therefore, the previous expression is rather |
||
|
<math display="block">\mathbf{u} \cdot \nabla \left({\frac{1}{2}}u^2 + \phi + \frac{p}{\rho}\right) = \frac{p}{\rho}\nabla \cdot \mathbf{u}</math> |
||
The right-hand side appears on the energy equation in convective form, which on the steady state reads: |
The right-hand side appears on the energy equation in convective form, which on the steady state reads: |
||
|
<math display="block">\mathbf u \cdot \nabla e = - \frac{p}{\rho} \nabla \cdot \mathbf u </math> |
||
The energy equation therefore becomes: |
The energy equation therefore becomes: |
||
|
<math display="block">\mathbf u \cdot \nabla \left( e + \frac p \rho + \frac 1 2 u^2 + \phi \right) = 0, </math> |
||
so that the internal specific energy now features in the head. |
so that the internal specific energy now features in the head. |
||
| Line 804: | Line 700: | ||
Since the external field potential is usually small compared to the other terms, it is convenient to group the latter ones in the [[total enthalpy]]: |
Since the external field potential is usually small compared to the other terms, it is convenient to group the latter ones in the [[total enthalpy]]: |
||
|
<math display="block"> h^t \equiv e + \frac p \rho + \frac 1 2 u^2</math> |
||
and the [[Bernoulli invariant]] for an inviscid gas flow is: |
and the [[Bernoulli invariant]] for an inviscid gas flow is: |
||
|
<math display="block"> b_g \equiv h^t + \phi = b_l + e , </math> |
||
which can be written as: |
which can be written as: |
||
|
<math display="block">\mathbf u \cdot \nabla b_g = 0</math> |
||
That is, '''the energy balance for a steady inviscid flow in an external conservative field states that the sum of the total enthalpy and the external potential is constant along a streamline'''. |
That is, '''the energy balance for a steady inviscid flow in an external conservative field states that the sum of the total enthalpy and the external potential is constant along a streamline'''. |
||
| Line 818: | Line 714: | ||
In the usual case of small potential field, simply: |
In the usual case of small potential field, simply: |
||
|
<math display="block">\mathbf u \cdot \nabla h^t \sim 0</math> |
||
===Friedmann form and Crocco form=== |
===Friedmann form and Crocco form=== |
||
| Line 824: | Line 720: | ||
By substituting the pressure gradient with the entropy and enthalpy gradient, according to the first law of thermodynamics in the enthalpy form: |
By substituting the pressure gradient with the entropy and enthalpy gradient, according to the first law of thermodynamics in the enthalpy form: |
||
|
<math display="block">v \nabla p = -T \nabla s + \nabla h</math> |
||
in the convective form of Euler momentum equation, one arrives to: |
in the convective form of Euler momentum equation, one arrives to: |
||
|
<math display="block">\frac{D\mathbf u}{Dt}=T \nabla\,s-\nabla \,h</math> |
||
[[Alexander Friedmann|Friedmann]] deduced this equation for the particular case of a [[perfect gas]] and published it in 1922.{{sfn|Friedmann|1934|p=198|loc=Eq 91}} However, this equation is general for an inviscid nonconductive fluid and no equation of state is implicit in it. |
[[Alexander Friedmann|Friedmann]] deduced this equation for the particular case of a [[perfect gas]] and published it in 1922.{{sfn|Friedmann|1934|p=198|loc=Eq 91}} However, this equation is general for an inviscid nonconductive fluid and no equation of state is implicit in it. |
||
| Line 834: | Line 730: | ||
On the other hand, by substituting the enthalpy form of the first law of thermodynamics in the rotational form of Euler momentum equation, one obtains: |
On the other hand, by substituting the enthalpy form of the first law of thermodynamics in the rotational form of Euler momentum equation, one obtains: |
||
|
<math display="block">\frac{\partial\mathbf{u}}{\partial t} + \frac{1}{2} \nabla\left(u^2\right) + (\nabla \times \mathbf{u}) \times \mathbf{u} + \frac{\nabla p}{\rho} = \mathbf{g}</math> |
||
and by defining the specific total enthalpy: |
and by defining the specific total enthalpy: |
||
|
<math display="block">h^t = h + \frac{1}{2}u^2</math> |
||
one arrives to the [[Crocco's theorem|Crocco–Vazsonyi form]]{{sfn|Henderson|2000|p=177|loc=par. 2.12 Crocco's theorem}} (Crocco, 1937) of the Euler momentum equation: |
one arrives to the [[Crocco's theorem|Crocco–Vazsonyi form]]{{sfn|Henderson|2000|p=177|loc=par. 2.12 Crocco's theorem}} (Crocco, 1937) of the Euler momentum equation: |
||
|
<math display="block">\frac{\partial \mathbf{ u}}{\partial t} + (\nabla \times \mathbf u) \times \mathbf u - T \nabla s + \nabla h^t = \mathbf{g}</math> |
||
In the steady case the two variables entropy and total enthalpy are particularly useful since Euler equations can be recast into the Crocco's form: |
In the steady case the two variables entropy and total enthalpy are particularly useful since Euler equations can be recast into the Crocco's form: |
||
|
<math display="block">\left\{\begin{align} |
||
\mathbf{u} \times \nabla \times \mathbf{u} + T\nabla s - \nabla h^t &= \mathbf{g} \\ |
\mathbf{u} \times \nabla \times \mathbf{u} + T\nabla s - \nabla h^t &= \mathbf{g} \\ |
||
\mathbf{u} \cdot \nabla s &= 0 \\ |
\mathbf{u} \cdot \nabla s &= 0 \\ |
||
| Line 854: | Line 750: | ||
Finally if the flow is also isothermal: |
Finally if the flow is also isothermal: |
||
|
<math display="block">T \nabla s = \nabla (T s)</math> |
||
by defining the specific total [[Gibbs free energy]]: |
by defining the specific total [[Gibbs free energy]]: |
||
|
<math display="block"> g^t \equiv h^t + Ts </math> |
||
the Crocco's form can be reduced to: |
the Crocco's form can be reduced to: |
||
|
<math display="block">\left\{\begin{align} |
||
\mathbf{u} \times \nabla \times \mathbf{u} - \nabla g^t &= \mathbf{g} \\ |
\mathbf{u} \times \nabla \times \mathbf{u} - \nabla g^t &= \mathbf{g} \\ |
||
\mathbf{u} \cdot \nabla g^t &= 0 |
\mathbf{u} \cdot \nabla g^t &= 0 |
||
| Line 880: | Line 776: | ||
Starting from the simplest case, one consider a steady free conservation equation in conservation form in the space domain: |
Starting from the simplest case, one consider a steady free conservation equation in conservation form in the space domain: |
||
|
<math display="block">\nabla \cdot \mathbf F = \mathbf 0 </math> |
||
where in general '''F''' is the flux matrix. By integrating this local equation over a fixed volume V<sub>m</sub>, it becomes: |
where in general '''F''' is the flux matrix. By integrating this local equation over a fixed volume V<sub>m</sub>, it becomes: |
||
|
<math display="block"> \int_{V_m} \nabla \cdot \mathbf F \,dV = \mathbf 0.</math> |
||
Then, basing on the [[divergence theorem]], we can transform this integral in a boundary integral of the flux: |
Then, basing on the [[divergence theorem]], we can transform this integral in a boundary integral of the flux: |
||
|
<math display="block"> \oint_{\partial V_m} \mathbf F \,ds = \mathbf 0.</math> |
||
This ''global form'' simply states that there is no net flux of a conserved quantity passing through a region in the case steady and without source. In 1D the volume reduces to an [[interval (mathematics)|interval]], its boundary being its extrema, then the divergence theorem reduces to the [[fundamental theorem of calculus]]: |
This ''global form'' simply states that there is no net flux of a conserved quantity passing through a region in the case steady and without source. In 1D the volume reduces to an [[interval (mathematics)|interval]], its boundary being its extrema, then the divergence theorem reduces to the [[fundamental theorem of calculus]]: |
||
|
<math display="block"> \int_{x_m}^{x_{m+1}} \mathbf F(x') \,dx' = \mathbf 0,</math> |
||
that is the simple [[finite difference equation]], known as the ''jump relation'': |
that is the simple [[finite difference equation]], known as the ''jump relation'': |
||
|
<math display="block"> \Delta \mathbf F = \mathbf 0.</math> |
||
That can be made explicit as: |
That can be made explicit as: |
||
|
<math display="block"> \mathbf F_{m+1} - \mathbf F_m = \mathbf 0</math> |
||
where the notation employed is: |
where the notation employed is: |
||
|
<math display="block"> \mathbf F_{m} = \mathbf F(x_m).</math> |
||
Or, if one performs an indefinite integral: |
Or, if one performs an indefinite integral: |
||
|
<math display="block"> \mathbf F - \mathbf F_0 = \mathbf 0.</math> |
||
On the other hand, a transient conservation equation: |
On the other hand, a transient conservation equation: |
||
|
<math display="block">{\partial y \over \partial t} + \nabla \cdot \mathbf F = \mathbf 0 </math> |
||
brings to a jump relation: |
brings to a jump relation: |
||
|
<math display="block"> \frac{dx}{dt} \, \Delta u = \Delta \mathbf F.</math> |
||
For one-dimensional Euler equations the conservation variables and the flux are the vectors: |
For one-dimensional Euler equations the conservation variables and the flux are the vectors: |
||
|
<math display="block">\mathbf y = \begin{pmatrix} \frac{1}{v} \\ j \\ E^t \end{pmatrix}, </math> |
||
|
<math display="block">\mathbf F = \begin{pmatrix} j \\ v j^2 + p \\ v j \left(E^t + p\right) \end{pmatrix}, </math> |
||
where: |
where: |
||
| Line 929: | Line 825: | ||
In the one dimensional case the correspondent jump relations, called the [[Rankine–Hugoniot equation]]s, are:<{{sfn|Chorin|Marsden|2013|p=122|loc= par. 3.2 Shocks}} |
In the one dimensional case the correspondent jump relations, called the [[Rankine–Hugoniot equation]]s, are:<{{sfn|Chorin|Marsden|2013|p=122|loc= par. 3.2 Shocks}} |
||
|
<math display="block">\left\{\begin{align} |
||
\frac{dx}{dt}\Delta \left(\frac{1}{v}\right) &= \Delta j\\[1.2ex] |
\frac{dx}{dt}\Delta \left(\frac{1}{v}\right) &= \Delta j\\[1.2ex] |
||
\frac{dx}{dt}\Delta j &= \Delta(vj^2 + p)\\[1.2ex] |
\frac{dx}{dt} \Delta j &= \Delta(vj^2 + p)\\[1.2ex] |
||
\frac{dx}{dt}\Delta E^t &= \Delta(jv(E^t + p)) |
\frac{dx}{dt}\Delta E^t &= \Delta(jv(E^t + p)). |
||
\end{align}\right |
\end{align}\right.</math> |
||
In the steady one dimensional case the become simply: |
In the steady one dimensional case the become simply: |
||
|
<math display="block">\left\{\begin{align} |
||
\Delta j &= 0\\[1.2ex] |
\Delta j &= 0\\[1.2ex] |
||
\Delta\left(v j^2 + p\right) &= 0 \\[1.2ex] |
\Delta\left(v j^2 + p\right) &= 0 \\[1.2ex] |
||
\Delta\left(j\left(\frac{E^t}{\rho} + \frac{p}{\rho}\right)\right) &= 0 |
\Delta\left(j\left(\frac{E^t}{\rho} + \frac{p}{\rho}\right)\right) &= 0. |
||
\end{align}\right |
\end{align}\right.</math> |
||
Thanks to the mass difference equation, the energy difference equation can be simplified without any restriction: |
Thanks to the mass difference equation, the energy difference equation can be simplified without any restriction: |
||
|
<math display="block">\left\{\begin{align} |
||
\Delta j &= 0 \\[1.2ex] |
\Delta j &= 0 \\[1.2ex] |
||
\Delta\left(vj^2 + p\right) &= 0 \\[1.2ex] |
\Delta\left(vj^2 + p\right) &= 0 \\[1.2ex] |
||
| Line 955: | Line 851: | ||
These are the usually expressed in the convective variables: |
These are the usually expressed in the convective variables: |
||
|
<math display="block">\left\{\begin{align} |
||
\Delta j &= 0 \\[1.2ex] |
\Delta j &= 0 \\[1.2ex] |
||
\Delta\left(\frac{u^2}{v} + p\right) &= 0 \\[1.2ex] |
\Delta\left(\frac{u^2}{v} + p\right) &= 0 \\[1.2ex] |
||
\Delta\left(e + \frac{1}{2}u^2 + pv\right) &= 0 |
\Delta\left(e + \frac{1}{2}u^2 + pv\right) &= 0, |
||
\end{align}\right. |
\end{align}\right.</math> |
||
where: |
where: |
||
| Line 968: | Line 864: | ||
The former mass and momentum equations by substitution lead to the Rayleigh equation: |
The former mass and momentum equations by substitution lead to the Rayleigh equation: |
||
|
<math display="block"> \frac{\Delta p}{\Delta v} = - \frac {u_0^2}{v_0}. </math> |
||
Since the second term is a constant, the Rayleigh equation always describes a simple [[line (geometry)|line]] in the [[pressure volume diagram|pressure volume plane]] not dependent of any equation of state, i.e. the [[Rayleigh line]]. By substitution in the Rankine–Hugoniot equations, that can be also made explicit as: |
Since the second term is a constant, the Rayleigh equation always describes a simple [[line (geometry)|line]] in the [[pressure volume diagram|pressure volume plane]] not dependent of any equation of state, i.e. the [[Rayleigh line]]. By substitution in the Rankine–Hugoniot equations, that can be also made explicit as: |
||
|
<math display="block">\left\{\begin{align} |
||
\rho u &= \rho_0 u_0 \\[1.2ex] |
\rho u &= \rho_0 u_0 \\[1.2ex] |
||
\rho u^2 + p &= \rho_0 u_0^2 + p_0 \\[1.2ex] |
\rho u^2 + p &= \rho_0 u_0^2 + p_0 \\[1.2ex] |
||
e + \frac{1}{2}u^2 + \frac{p}{\rho} &= e_0 + \frac{1}{2}u_0^2 + \frac{p_0}{\rho_0} |
e + \frac{1}{2}u^2 + \frac{p}{\rho} &= e_0 + \frac{1}{2}u_0^2 + \frac{p_0}{\rho_0}. |
||
\end{align}\right |
\end{align}\right.</math> |
||
One can also obtain the kinetic equation and to the Hugoniot equation. The analytical passages are not shown here for brevity. |
One can also obtain the kinetic equation and to the Hugoniot equation. The analytical passages are not shown here for brevity. |
||
| Line 984: | Line 880: | ||
These are respectively: |
These are respectively: |
||
|
<math display="block">\left\{\begin{align} |
||
u^2(v, p) &= u_0^2 + (p - p_0)(v_0 + v) \\[1.2ex] |
u^2(v, p) &= u_0^2 + (p - p_0)(v_0 + v) \\[1.2ex] |
||
e(v, p) &= e_0 + \ |
e(v, p) &= e_0 + \tfrac{1}{2} (p + p_0)(v_0 - v). |
||
\end{align}\right |
\end{align}\right.</math> |
||
The Hugoniot equation, coupled with the fundamental equation of state of the material: |
The Hugoniot equation, coupled with the fundamental equation of state of the material: |
||
|
<math display="block"> e = e(v,p)</math> |
||
describes in general in the pressure volume plane a curve passing by the conditions (v<sub>0</sub>, p<sub>0</sub>), i.e. the [[Hugoniot curve]], whose shape strongly depends on the type of material considered. |
describes in general in the pressure volume plane a curve passing by the conditions (v<sub>0</sub>, p<sub>0</sub>), i.e. the [[Hugoniot curve]], whose shape strongly depends on the type of material considered. |
||
| Line 997: | Line 893: | ||
It is also customary to define a ''Hugoniot function'':{{sfn|Henderson|2000|p=167|loc= par. 2.96 The Bethe–Weyl theorem}} |
It is also customary to define a ''Hugoniot function'':{{sfn|Henderson|2000|p=167|loc= par. 2.96 The Bethe–Weyl theorem}} |
||
|
<math display="block"> \mathfrak h (v,s) \equiv e(v,s) - e_0 + \tfrac{1}{2} (p(v,s) + p_0)(v - v_0)</math> |
||
allowing to quantify deviations from the Hugoniot equation, similarly to the previous definition of the ''hydraulic head'', useful for the deviations from the Bernoulli equation. |
allowing to quantify deviations from the Hugoniot equation, similarly to the previous definition of the ''hydraulic head'', useful for the deviations from the Bernoulli equation. |
||
| Line 1,004: | Line 900: | ||
On the other hand, by integrating a generic conservation equation: |
On the other hand, by integrating a generic conservation equation: |
||
|
<math display="block"> \frac {\partial \mathbf y}{\partial t} + \nabla \cdot \mathbf F = \mathbf s </math> |
||
on a fixed volume V<sub>m</sub>, and then basing on the [[divergence theorem]], it becomes: |
on a fixed volume ''V<sub>m</sub>'', and then basing on the [[divergence theorem]], it becomes: |
||
|
<math display="block"> \frac {d}{dt} \int_{V_m} \mathbf y dV + \oint_{\partial V_m} \mathbf F \cdot \hat n ds = \mathbf S .</math> |
||
By integrating this equation also over a time interval: |
By integrating this equation also over a time interval: |
||
|
<math display="block"> \int_{V_m} \mathbf y(\mathbf r, t_{n+1}) \, dV - \int_{V_m} \mathbf y(\mathbf r, t_n) \, dV+ \int_{t_n}^{t_{n+1}} \oint_{\partial V_m} \mathbf F \cdot \hat n \, ds \, dt = \mathbf 0 .</math> |
||
Now by defining the node conserved quantity: |
Now by defining the node conserved quantity: |
||
|
<math display="block">\mathbf y_{m,n} \equiv \frac 1 {V_m} \int_{V_m} \mathbf y(\mathbf r, t_n) \, dV ,</math> |
||
we deduce the finite volume form: |
we deduce the finite volume form: |
||
|
<math display="block">\mathbf{y}_{m,n+1}=\mathbf{y}_{m,n} - \frac{1}{V_m} \int_{t_n}^{t_{n+1}} \oint_{\partial V_m} \mathbf{F} \cdot \hat{n}\, ds \, dt .</math> |
||
In particular, for Euler equations, once the conserved quantities have been determined, the convective variables are deduced by back substitution: |
In particular, for Euler equations, once the conserved quantities have been determined, the convective variables are deduced by back substitution: |
||
|
<math display="block">\begin{cases} |
||
\mathbf u_{m,n} |
\displaystyle \mathbf u_{m,n} = \frac{\mathbf j_{m,n}}{\rho_{m,n}} \\[1.2ex] |
||
e_{m,n} |
\displaystyle e_{m,n} = \frac{E^t_{m,n}}{\rho_{m,n}} - \frac{1}{2} u^2_{m,n}. |
||
\end{ |
\end{cases}</math> |
||
Then the explicit finite volume expressions of the original convective variables are:<{{sfn|Quartapelle|Auteri|2013|p=161|loc=par. 11.10: Forma differenziale: metodo dei volumi finiti}} |
Then the explicit finite volume expressions of the original convective variables are:<{{sfn|Quartapelle|Auteri|2013|p=161|loc=par. 11.10: Forma differenziale: metodo dei volumi finiti}} |
||
| Line 1,033: | Line 929: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Euler equations''' |
|title='''Euler equations'''<br/>(''Finite volume form'') |
||
|equation=<math>\left\{\begin{align} |
|equation=<math>\left\{\begin{align} |
||
\rho_{m,n+1} &= \rho_{m,n} - \frac{1}{V_m}\int_{t_n}^{t_{n+1}}\oint_{\partial V_m}\rho\mathbf{u} \cdot \hat{n}\, ds\, dt \\[1.2ex] |
\rho_{m,n+1} &= \rho_{m,n} - \frac{1}{V_m}\int_{t_n}^{t_{n+1}}\oint_{\partial V_m}\rho\mathbf{u} \cdot \hat{n}\, ds\, dt \\[1.2ex] |
||
| Line 1,052: | Line 948: | ||
For an ideal polytropic gas the fundamental [[equation of state]] is:{{sfn|Quartapelle|Auteri|2013|p=A-61|loc=Appendix E}} |
For an ideal polytropic gas the fundamental [[equation of state]] is:{{sfn|Quartapelle|Auteri|2013|p=A-61|loc=Appendix E}} |
||
|
<math display="block">e(v, s) = e_0 e^{(\gamma-1)m\left(s-s_0\right)} \left({v_0 \over v}\right)^{\gamma-1}</math> |
||
where <math>e</math> is the specific energy, <math>v</math> is the specific volume, <math>s</math> is the specific entropy, <math>m</math> is the molecular mass, <math>\gamma</math> here is considered a constant ([[polytropic process]]), and can be shown to correspond to the [[heat capacity ratio]]. This equation can be shown to be consistent with the usual equations of state employed by thermodynamics. |
where <math>e</math> is the specific energy, <math>v</math> is the specific volume, <math>s</math> is the specific entropy, <math>m</math> is the molecular mass, <math>\gamma</math> here is considered a constant ([[polytropic process]]), and can be shown to correspond to the [[heat capacity ratio]]. This equation can be shown to be consistent with the usual equations of state employed by thermodynamics. |
||
| Line 1,060: | Line 956: | ||
|By the thermodynamic definition of temperature: |
|By the thermodynamic definition of temperature: |
||
|
<math display="block">T(e) \equiv {\partial e \over \partial s} = (\gamma - 1) m e</math> |
||
Where the temperature is measured in energy units. At first, note that by combining these two equations one can deduce the '''[[ideal gas law]]''': |
Where the temperature is measured in energy units. At first, note that by combining these two equations one can deduce the '''[[ideal gas law]]''': |
||
|
<math display="block">p v = m T</math> |
||
or, in the usual form: |
or, in the usual form: |
||
|
<math display="block">p = n T</math> |
||
where: <math>n \equiv \frac m v</math> is the number density of the material. On the other hand the ideal gas law is less strict than the original fundamental equation of state considered. |
where: <math>n \equiv \frac m v</math> is the number density of the material. On the other hand the ideal gas law is less strict than the original fundamental equation of state considered. |
||
| Line 1,074: | Line 970: | ||
Now consider the molar heat capacity associated to a process ''x'': |
Now consider the molar heat capacity associated to a process ''x'': |
||
|
<math display="block">c_x = \left(m T {\partial s \over \partial T}\right)_x</math> |
||
according to the first law of thermodynamics: |
according to the first law of thermodynamics: |
||
|
<math display="block">d e(v,s)=-p dv + T \, ds</math> |
||
it can be simply expressed as: |
it can be simply expressed as: |
||
|
<math display="block">c_x \equiv m \left({\partial e \over \partial T}\right)_x + m p \left({\partial v \over \partial T}\right)_x</math> |
||
Now inverting the equation for temperature T(e) we deduce that for an ideal polytropic gas the isochoric heat capacity is a constant: |
Now inverting the equation for temperature T(e) we deduce that for an ideal polytropic gas the isochoric heat capacity is a constant: |
||
|
<math display="block">c_v \equiv m \left({\partial e \over \partial T}\right)_v = m {d e \over dT} = \frac {1}{(\gamma -1)}</math> |
||
and similarly for an ideal polytropic gas the isobaric heat capacity results constant: |
and similarly for an ideal polytropic gas the isobaric heat capacity results constant: |
||
|
<math display="block">c_p \equiv m \left({\partial e \over \partial T}\right)_p + m p \left({\partial v \over \partial T}\right)_p = m {d e \over dT} + p \left({\partial v \over \partial T}\right)_p = \frac {1}{(\gamma -1)} + 1</math> |
||
This brings to two important [[relations between heat capacities]]: the constant gamma actually represents the '''[[heat capacity ratio]]''' in the ideal polytropic gas: |
This brings to two important [[relations between heat capacities]]: the constant gamma actually represents the '''[[heat capacity ratio]]''' in the ideal polytropic gas: |
||
|
<math display="block">\frac {c_p}{c_v}= \gamma</math> |
||
and one also arrives to the '''Meyer's relation''': |
and one also arrives to the '''Meyer's relation''': |
||
|
<math display="block">c_p = c_v+1</math> |
||
The specific energy is then, by inverting the relation T(e): |
The specific energy is then, by inverting the relation T(e): |
||
|
<math display="block">e(T) = \frac {mT} {\gamma - 1} = c_v m T</math> |
||
The specific enthalpy results by substitution of the latter and of the ideal gas law: |
The specific enthalpy results by substitution of the latter and of the ideal gas law: |
||
|
<math display="block">h(T) \equiv e(T) + (p v)(T) = c_v m T + m T = c_p m T</math> |
||
|style = border: 1px solid lightgray; width: 90%; |
|style = border: 1px solid lightgray; width: 90%; |
||
| Line 1,114: | Line 1,010: | ||
From this equation one can derive the equation for pressure by its thermodynamic definition: |
From this equation one can derive the equation for pressure by its thermodynamic definition: |
||
|
<math display="block">p(v,e) \equiv - {\partial e \over \partial v} = (\gamma - 1) \frac e v</math> |
||
By inverting it one arrives to the mechanical equation of state: |
By inverting it one arrives to the mechanical equation of state: |
||
|
<math display="block">e(v,p) = \frac {pv}{\gamma - 1}</math> |
||
Then for an ideal gas the compressible Euler equations can be simply expressed in the ''mechanical'' or ''primitive variables'' specific volume, flow velocity and pressure, by taking the set of the equations for a thermodynamic system and modifying the energy equation into a pressure equation through this mechanical equation of state. At last, in convective form they result: |
Then for an ideal gas the compressible Euler equations can be simply expressed in the ''mechanical'' or ''primitive variables'' specific volume, flow velocity and pressure, by taking the set of the equations for a thermodynamic system and modifying the energy equation into a pressure equation through this mechanical equation of state. At last, in convective form they result: |
||
| Line 1,124: | Line 1,020: | ||
{{Equation box 1 |
{{Equation box 1 |
||
|indent=: |
|indent=: |
||
|title='''Euler equations for an ideal polytropic gas''' |
|title='''Euler equations for an ideal polytropic gas'''<br/>(''convective form''){{sfn|Toro|1999|p= 91|loc=par 3.1.2 Nonconservative formulations}} |
||
|equation=<math>\left\{\begin{align} |
|equation=<math>\left\{\begin{align} |
||
{Dv \over Dt} &= v\nabla \cdot \mathbf{u} \\[1.2ex] |
{Dv \over Dt} &= v\nabla \cdot \mathbf{u} \\[1.2ex] |
||
| Line 1,138: | Line 1,034: | ||
and in one-dimensional quasilinear form they results: |
and in one-dimensional quasilinear form they results: |
||
|
<math display="block"> \frac{\partial \mathbf y}{\partial t} + \mathbf A \frac{\partial \mathbf y}{\partial x} = {\mathbf 0}. </math> |
||
where the conservative vector variable is: |
where the conservative vector variable is: |
||
|
<math display="block">{\mathbf y}=\begin{pmatrix}v\\ u \\p \end{pmatrix}</math> |
||
and the corresponding jacobian matrix is:{{sfn|Zingale|2013|p=}} |
and the corresponding jacobian matrix is:{{sfn|Zingale|2013|p=}}{{sfn|Toro|1999|p= 92}} |
||
|
<math display="block">{\mathbf A}=\begin{pmatrix}u & -v & 0 \\ 0 & u & v \\ 0 & \gamma p & u \end{pmatrix}.</math> |
||
=== Steady flow in material coordinates {{anchor|Steady flow in streamline coordinates}} === |
=== Steady flow in material coordinates {{anchor|Steady flow in streamline coordinates}} === |
||
In the case of steady flow, it is convenient to choose the [[Frenet–Serret frame]] along a [[Streamlines, streaklines, and pathlines|streamline]] as the [[coordinate system]] for describing the steady [[momentum]] Euler equation:{{sfn|Fay|1994|pp=150-152}} |
In the case of steady flow, it is convenient to choose the [[Frenet–Serret frame]] along a [[Streamlines, streaklines, and pathlines|streamline]] as the [[coordinate system]] for describing the steady [[momentum]] Euler equation:{{sfn|Fay|1994|pp=150-152}} |
||
|
<math display="block"> |
||
\boldsymbol{u}\cdot\nabla \boldsymbol{u} = - \frac{1}{\rho} \nabla p, |
\boldsymbol{u}\cdot\nabla \boldsymbol{u} = - \frac{1}{\rho} \nabla p, |
||
</math> |
</math> |
||
| Line 1,157: | Line 1,053: | ||
Let <math>\left\{ \mathbf e_s, \mathbf e_n, \mathbf e_b \right\}</math> be a Frenet–Serret [[orthonormal basis]] which consists of a tangential unit vector, a normal unit vector, and a binormal unit vector to the streamline, respectively. Since a streamline is a curve that is tangent to the velocity vector of the flow, the left-hand side of the above equation, the [[convective derivative]] of velocity, can be described as follows: |
Let <math>\left\{ \mathbf e_s, \mathbf e_n, \mathbf e_b \right\}</math> be a Frenet–Serret [[orthonormal basis]] which consists of a tangential unit vector, a normal unit vector, and a binormal unit vector to the streamline, respectively. Since a streamline is a curve that is tangent to the velocity vector of the flow, the left-hand side of the above equation, the [[convective derivative]] of velocity, can be described as follows: |
||
|
<math display="block">\begin{align} |
||
\boldsymbol{u}\cdot\nabla \boldsymbol{u} \\ |
\boldsymbol{u}\cdot\nabla \boldsymbol{u} \\[1ex] |
||
&= u\frac{\partial}{\partial s}(u\boldsymbol{e}_s) |
&= u\frac{\partial}{\partial s}(u\boldsymbol{e}_s) |
||
&(\boldsymbol{u} = u \boldsymbol{e}_s,~ {\partial / \partial s} \equiv \boldsymbol{e}_s \cdot \nabla) \\ |
&(\boldsymbol{u} = u \boldsymbol{e}_s,~ {\partial / \partial s} \equiv \boldsymbol{e}_s \cdot \nabla) \\[1ex] |
||
&= u\frac{\partial u}{\partial s}\boldsymbol{e}_s + \frac{u^2}{R}\boldsymbol{e}_n |
&= u\frac{\partial u}{\partial s}\boldsymbol{e}_s + \frac{u^2}{R}\boldsymbol{e}_n |
||
&(\because~ \frac{\partial\boldsymbol{e}_s}{\partial s} = \frac{1}{R}\boldsymbol{e}_n), |
&(\because~ \frac{\partial\boldsymbol{e}_s}{\partial s} = \frac{1}{R}\boldsymbol{e}_n), |
||
| Line 1,168: | Line 1,064: | ||
Therefore, the momentum part of the Euler equations for a steady flow is found to have a simple form: |
Therefore, the momentum part of the Euler equations for a steady flow is found to have a simple form: |
||
|
<math display="block">\begin{cases} |
||
\displaystyle u\frac{\partial u}{\partial s} = -\frac{1}{\rho}\frac{\partial p}{\partial s},\\ |
\displaystyle u\frac{\partial u}{\partial s} = -\frac{1}{\rho}\frac{\partial p}{\partial s},\\ |
||
\displaystyle {u^2 \over R} = -\frac{1}{\rho}\frac{\partial p}{\partial n} &({\partial / \partial n}\equiv\boldsymbol{e}_n\cdot\nabla),\\ |
\displaystyle {u^2 \over R} = -\frac{1}{\rho}\frac{\partial p}{\partial n} &({\partial / \partial n}\equiv\boldsymbol{e}_n\cdot\nabla),\\ |
||
| Line 1,175: | Line 1,071: | ||
For [[barotropic]] flow <math>(\rho = \rho(p))</math>, [[Bernoulli's equation]] is derived from the first equation: |
For [[barotropic]] flow <math>(\rho = \rho(p))</math>, [[Bernoulli's equation]] is derived from the first equation: |
||
|
<math display="block">\frac{\partial}{\partial s}\left(\frac{u^2}{2} + \int\frac{\mathrm{d}p}{\rho}\right) = 0.</math> |
||
The second equation expresses that, in the case the streamline is curved, there should exist a [[pressure gradient]] normal to the streamline because the [[centripetal acceleration]] of the [[fluid parcel]] is only generated by the normal pressure gradient. |
The second equation expresses that, in the case the streamline is curved, there should exist a [[pressure gradient]] normal to the streamline because the [[centripetal acceleration]] of the [[fluid parcel]] is only generated by the normal pressure gradient. |
||
| Line 1,187: | Line 1,083: | ||
Let <math>r</math> be the distance from the center of curvature of the streamline, then the second equation is written as follows: |
Let <math>r</math> be the distance from the center of curvature of the streamline, then the second equation is written as follows: |
||
|
<math display="block"> |
||
\frac{\partial p}{\partial r} = \rho \frac{u^2}{r}~(>0), |
\frac{\partial p}{\partial r} = \rho \frac{u^2}{r}~(>0), |
||
</math> |
</math> |
||
| Line 1,193: | Line 1,089: | ||
where <math>{\partial / \partial r} = -{\partial /\partial n}.</math> |
where <math>{\partial / \partial r} = -{\partial /\partial n}.</math> |
||
This equation states:<blockquote> |
This equation states:<blockquote> |
||
In a steady flow of an [[inviscid]] [[fluid]] without external forces, the [[center of curvature]] of the streamline lies in the direction of decreasing radial pressure. |
''In a steady flow of an [[inviscid]] [[fluid]] without external forces, the [[center of curvature]] of the streamline lies in the direction of decreasing radial pressure.'' |
||
|
</blockquote> |
||
Although this relationship between the pressure field and flow curvature is very useful, it doesn't have a name in the English-language scientific literature.{{sfn|Babinsky|2003}} Japanese fluid-dynamicists call the relationship the "Streamline curvature theorem".{{sfn|Imai|1973|p=}} |
Although this relationship between the pressure field and flow curvature is very useful, it doesn't have a name in the English-language scientific literature.{{sfn|Babinsky|2003}} Japanese fluid-dynamicists call the relationship the "Streamline curvature theorem".{{sfn|Imai|1973|p=}} |
||
| Line 1,215: | Line 1,111: | ||
* [[Kelvin's circulation theorem]] |
* [[Kelvin's circulation theorem]] |
||
* [[Cauchy momentum equation|Cauchy equations]] |
* [[Cauchy momentum equation|Cauchy equations]] |
||
* [[Madelung equations]] |
|||
* [[Froude number]] |
* [[Froude number]] |
||
* [[Madelung equations]] |
|||
* [[Navier–Stokes equations]] |
* [[Navier–Stokes equations]] |
||
* [[Burgers equation]] |
* [[Burgers equation]] |
||
* [[Jeans equations]] |
|||
* [[Perfect fluid]] |
* [[Perfect fluid]] |
||
| Line 1,230: | Line 1,127: | ||
===Sources=== |
===Sources=== |
||
{{Refbegin|2|indent=yes}} |
{{Refbegin|2|indent=yes}} |
||
*{{cite book|last=Anderson|first=John |
*{{cite book|last=Anderson|first=John|title=Computational Fluid Dynamics|url=https://books.google.com/books?id=dJceAQAAIAAJ|year=1995|publisher=McGraw-Hill Education|isbn=978-0-07-001685-9}} |
||
*{{citation |
*{{citation | journal=Physics Education | first=Holger | last=Babinsky | date=November 2003 | url=http://www.iop.org/EJ/article/0031-9120/38/6/001/pe3_6_001.pdf | title=How do wings work? | volume=38 | issue=6 | pages=497–503 | doi=10.1088/0031-9120/38/6/001 | bibcode=2003PhyEd..38..497B | s2cid=1657792 }} |
||
*{{cite book|last1=Chorin|first1=Alexandre J. |
*{{cite book|last1=Chorin|first1=Alexandre J.|last2=Marsden|first2=Jerrold E.|title=A Mathematical Introduction to Fluid Mechanics|url=https://books.google.com/books?id=HBXSBwAAQBAJ|date=2013|publisher=Springer|isbn=978-1-4612-0883-9}} |
||
*{{cite journal|doi=10.1090/S0273-0979-07-01181-0|last=Christodoulou|first=Demetrios|title=The Euler Equations of Compressible Fluid Flow|journal=Bulletin of the American Mathematical Society|volume=44|issue=4|date=October 2007|url=https://www.ams.org/bull/2007-44-04/S0273-0979-07-01181-0/S0273-0979-07-01181-0.pdf|pages= |
*{{cite journal|doi=10.1090/S0273-0979-07-01181-0|last=Christodoulou|first=Demetrios|title=The Euler Equations of Compressible Fluid Flow|journal=Bulletin of the American Mathematical Society|volume=44|issue=4|date=October 2007|url=https://www.ams.org/bull/2007-44-04/S0273-0979-07-01181-0/S0273-0979-07-01181-0.pdf|pages=581–602|doi-access=free}} |
||
*{{cite journal|journal=Mémoires de l'académie des sciences de Berlin |
*{{cite journal|journal=Mémoires de l'académie des sciences de Berlin|volume=11|date=1757|pages=274–315|title=Principes généraux du mouvement des fluides|first=Leonhard|last=Euler|url=https://scholarlycommons.pacific.edu/euler-works/226|language=fr|trans-title=The General Principles of the Movement of Fluids}} |
||
*{{cite book|last=Fay|first=James A. |
*{{cite book|last=Fay|first=James A.|title=Introduction to Fluid Mechanics|url=https://books.google.com/books?id=XGVpue4954wC&pg=PA150|year=1994|publisher=MIT Press|isbn=978-0-262-06165-0}} |
||
*{{cite book |title=Handbook of Mathematical Fluid Dynamics – Volume 2 |editor1-last=Friedlander |editor1-first=S. |editor2-last=Serre |editor2-first=D. |isbn=978-0-444-51287-1 |year=2003 |publisher=Elsevier }} |
*{{cite book |title=Handbook of Mathematical Fluid Dynamics – Volume 2 |editor1-last=Friedlander |editor1-first=S. |editor2-last=Serre |editor2-first=D. |isbn=978-0-444-51287-1 |year=2003 |publisher=Elsevier }} |
||
*{{cite book|last=Friedmann|first= |
*{{cite book|last=Friedmann|first=A.|author-link=Alexander Friedmann|trans-title=An essay on hydrodynamics of compressible fluid|title=Опыт гидромеханики сжимаемой жидкости|language=ru|location=[[Saint Petersburg|Petrograd]]|orig-year=1922|date=1934|url=http://books.e-heritage.ru/book/10073889|editor-link=Nikolai Kochin|editor-first=Nikolai|editor-last=Kochin}} |
||
*{{cite journal |first1=J.D. |last1=Gibbon |first2=D.R. |last2=Moore |first3=J.T. |last3=Stuart |title=Exact, infinite energy, blow-up solutions of the three-dimensional Euler equations |journal=Nonlinearity |volume=16 |issue=5 |pages=1823–1831 |year=2003 |doi=10.1088/0951-7715/16/5/315 |bibcode = 2003Nonli..16.1823G |s2cid=250797052 }} |
*{{cite journal |first1=J.D. |last1=Gibbon |first2=D.R. |last2=Moore |first3=J.T. |last3=Stuart |authorlink3=J. T. Stuart|title=Exact, infinite energy, blow-up solutions of the three-dimensional Euler equations |journal=Nonlinearity |volume=16 |issue=5 |pages=1823–1831 |year=2003 |doi=10.1088/0951-7715/16/5/315 |bibcode = 2003Nonli..16.1823G |s2cid=250797052 }} |
||
*{{cite book|editor-last1=Ben-Dor|editor-first1=Gabi |
*{{cite book|editor-last1=Ben-Dor|editor-first1=Gabi|editor-last2=Igra|editor-first2=Ozer|editor-last3=Elperin|editor-first3=Tov|title=Handbook of Shock Waves, Three Volume Set|chapter-url=https://books.google.com/books?id=qcYjUc7A9KMC&pg=PA152|year=2000|publisher=Elsevier|isbn=978-0-08-053372-8|first=L.F.|last=Henderson|chapter=General Laws for the Propagation of Shock-waves through Matter}} |
||
*{{citation|title=An Introduction to the Incompressible Euler Equations |first=John K. |last=Hunter |date=25 September 2006|url=https://www.math.ucdavis.edu/~hunter/notes/euler.pdf|access-date=2019-05-31}} |
*{{citation |title=An Introduction to the Incompressible Euler Equations |first=John K. |last=Hunter |date=25 September 2006 |url=https://www.math.ucdavis.edu/~hunter/notes/euler.pdf |access-date=2019-05-31 }} |
||
*{{cite book|author=今井 功 (IMAI, Isao)|title=『流体力学(前編)』|trans-title=Fluid Dynamics 1|publisher=裳華房 (Shoukabou)|date=November 1973 |
*{{cite book|author=今井 功 (IMAI, Isao)|title=『流体力学(前編)』|trans-title=Fluid Dynamics 1|publisher=裳華房 (Shoukabou)|date=November 1973 |
||
|isbn=4-7853-2314-0|language=Japanese|ref={{sfnref|Imai|1973}} }} |
|isbn=4-7853-2314-0|language=Japanese|ref={{sfnref|Imai|1973}} }} |
||
*{{cite book|last1=Landau|first1=L D |
*{{cite book|last1=Landau|first1=L D|last2=Lifshitz|first2=E. M.|title=Fluid Mechanics|url=https://books.google.com/books?id=CeBbAwAAQBAJ&pg=PA4|year=2013|publisher=Elsevier|isbn=978-1-4831-4050-6}} |
||
*{{cite book | title=Mathematical Theory of Incompressible Nonviscous Fluids | last1=Marchioro |first1=C. |last2=Pulvirenti |first2=M. |isbn=0-387-94044-8 |series=Applied Mathematical Sciences |volume=96 |year=1994 |publisher=Springer |location=New York }} |
*{{cite book | title=Mathematical Theory of Incompressible Nonviscous Fluids | last1=Marchioro |first1=C. |last2=Pulvirenti |first2=M. |isbn=0-387-94044-8 |series=Applied Mathematical Sciences |volume=96 |year=1994 |publisher=Springer |location=New York }} |
||
*{{cite book|last1=Quartapelle|first1=Luigi |
*{{cite book|last1=Quartapelle|first1=Luigi|last2=Auteri|first2=Franco|title=Fluidodinamica comprimibile|url=https://books.google.com/books?id=VGMPnQEACAAJ|year=2013|publisher=CEA|language=it|isbn=978-88-08-18558-7|trans-title=Compressible Fluid Dynamics}} |
||
*{{cite book|last=Toro|first=E. F. |
*{{cite book|last=Toro|first=E. F.|title=Riemann Solvers and Numerical Methods for Fluid Dynamics: A Practical Introduction|url=https://books.google.com/books?id=FbemQgAACAAJ|year=1999|publisher=Springer|isbn=978-3-540-65966-2}} |
||
*{{citation|publisher=Sapienza - Universit`a di Roma |
*{{citation|publisher=Sapienza - Universit`a di Roma|title=Metodi di analisi delle turbomacchine|first1=Mauro|last1=Valorani|first2=Francesco|last2=Nasuti|url=http://web2srv.ing.uniroma1.it/~m_valorani/GasTurbines_LM_files/DispenseTurboMacchine.pdf|access-date=2019-05-31|date=n.d.|archive-date=2022-05-16|archive-url=https://web.archive.org/web/20220516185800/http://web2srv.ing.uniroma1.it/~m_valorani/GasTurbines_LM_files/DispenseTurboMacchine.pdf|url-status=dead}} |
||
*{{citation|first=M. |
*{{citation|first=M.|last=Zingale|title=Notes on the Euler equations|date=16 April 2013|url=http://bender.astro.sunysb.edu/hydro_by_example/compressible/Euler.pdf|access-date=2019-05-31|archive-date=2015-06-19|archive-url=https://web.archive.org/web/20150619141500/http://bender.astro.sunysb.edu/hydro_by_example/compressible/Euler.pdf|url-status=dead}} |
||
{{Refend}} |
{{Refend}} |
||
===Further reading=== |
===Further reading=== |
||
{{Refbegin}} |
{{Refbegin}} |
||
* {{cite book| isbn=978-3-319-59694-5 |last1=Badin|first1=G.|last2=Crisciani|first2=F.| title=Variational Formulation of Fluid and Geophysical Fluid Dynamics - Mechanics, Symmetries and Conservation Laws - | publisher=Springer| year=2018 | pages=218 | doi= 10.1007/978-3-319-59695-2|s2cid=125902566}} |
* {{cite book| isbn=978-3-319-59694-5 |last1=Badin|first1=G.|last2=Crisciani|first2=F.| title=Variational Formulation of Fluid and Geophysical Fluid Dynamics - Mechanics, Symmetries and Conservation Laws - | publisher=Springer| year=2018 | pages=218 | doi= 10.1007/978-3-319-59695-2|bibcode=2018vffg.book.....B |s2cid=125902566}} |
||
*{{cite book | first=G. K. | last=Batchelor | title=An Introduction to Fluid Dynamics | year=1967 | publisher=Cambridge University Press | isbn=0-521-66396-2 }} |
*{{cite book | first=G. K. | last=Batchelor | title=An Introduction to Fluid Dynamics | year=1967 | publisher=Cambridge University Press | isbn=0-521-66396-2 }} |
||
*{{cite book | first=Philip A. | last=Thompson| year=1972 | title=Compressible Fluid Flow | publisher=McGraw-Hill | location=New York | isbn=0-07-064405-5 }} |
*{{cite book | first=Philip A. | last=Thompson| year=1972 | title=Compressible Fluid Flow | publisher=McGraw-Hill | location=New York | isbn=0-07-064405-5 }} |
||
| Line 1,261: | Line 1,158: | ||
{{Authority control}} |
{{Authority control}} |
||
[[Category: |
[[Category:Eponymous equations of physics]] |
||
[[Category:Equations of fluid dynamics]] |
[[Category:Equations of fluid dynamics]] |
||
[[Category:Leonhard Euler]] |
[[Category:Leonhard Euler]] |
||

Influid dynamics, the Euler equations are a set of partial differential equations governing adiabatic and inviscid flow. They are named after Leonhard Euler. In particular, they correspond to the Navier–Stokes equations with zero viscosity and zero thermal conductivity.[1]
The Euler equations can be applied to incompressible and compressible flows. The incompressible Euler equations consist of Cauchy equations for conservation of mass and balance of momentum, together with the incompressibility condition that the flow velocity is a solenoidal field. The compressible Euler equations consist of equations for conservation of mass, balance of momentum, and balance of energy, together with a suitable constitutive equation for the specific energy density of the fluid. Historically, only the equations of conservation of mass and balance of momentum were derived by Euler. However, fluid dynamics literature often refers to the full set of the compressible Euler equations – including the energy equation – as "the compressible Euler equations".[2]
The mathematical characters of the incompressible and compressible Euler equations are rather different. For constant fluid density, the incompressible equations can be written as a quasilinear advection equation for the fluid velocity together with an elliptic Poisson's equation for the pressure. On the other hand, the compressible Euler equations form a quasilinear hyperbolic system of conservation equations.
The Euler equations can be formulated in a "convective form" (also called the "Lagrangian form") or a "conservation form" (also called the "Eulerian form"). The convective form emphasizes changes to the state in a frame of reference moving with the fluid. The conservation form emphasizes the mathematical interpretation of the equations as conservation equations for a control volume fixed in space (which is useful from a numerical point of view).
The Euler equations first appeared in published form in Euler's article "Principes généraux du mouvement des fluides", published in Mémoires de l'Académie des Sciences de Berlin in 1757[3] (although Euler had previously presented his work to the Berlin Academy in 1752).[4] The Euler equations were among the first partial differential equations to be written down, after the wave equation. In Euler's original work, the system of equations consisted of the momentum and continuity equations, and thus was underdetermined except in the case of an incompressible flow. An additional equation, which was called the adiabatic condition, was supplied by Pierre-Simon Laplace in 1816.
During the second half of the 19th century, it was found that the equation related to the balance of energy must at all times be kept for compressible flows, and the adiabatic condition is a consequence of the fundamental laws in the case of smooth solutions. With the discovery of the special theory of relativity, the concepts of energy density, momentum density, and stress were unified into the concept of the stress–energy tensor, and energy and momentum were likewise unified into a single concept, the energy–momentum vector.[4]
In convective form (i.e., the form with the convective operator made explicit in the momentum equation), the incompressible Euler equations in case of density constant in time and uniform in space are:[5]

where:
 is the flow velocity vector, with components in an N-dimensional space
is the flow velocity vector, with components in an N-dimensional space  ,
, , for a generic function (or field)
, for a generic function (or field)  denotes its material derivative in time with respect to the advective field
denotes its material derivative in time with respect to the advective field  and
and is the gradient of the specific (with the sense of per unit mass) thermodynamic work, the internal source term, and
is the gradient of the specific (with the sense of per unit mass) thermodynamic work, the internal source term, and is the flow velocity divergence.
is the flow velocity divergence. represents body accelerations (per unit mass) acting on the continuum, for example gravity, inertial accelerations, electric field acceleration, and so on.
represents body accelerations (per unit mass) acting on the continuum, for example gravity, inertial accelerations, electric field acceleration, and so on.
The first equation is the Euler momentum equation with uniform density (for this equation it could also not be constant in time). By expanding the material derivative, the equations become:

In fact for a flow with uniform density 



So the case of constant and uniform density is the only one not requiring the continuity equation as additional equation regardless of the presence or absence of the incompressible constraint. In fact, the case of incompressible Euler equations with constant and uniform density discussed here is a toy model featuring only two simplified equations, so it is ideal for didactical purposes even if with limited physical relevance.
The equations above thus represent respectively conservation of mass (1 scalar equation) and momentum (1 vector equation containing 

In a coordinate system given by 





where the 


Although Euler first presented these equations in 1755, many fundamental questions or concepts about them remain unanswered.
In three space dimensions, in certain simplified scenarios, the Euler equations produce singularities.[6]
Smooth solutions of the free (in the sense of without source term: g=0) equations satisfy the conservation of specific kinetic energy:

In the one-dimensional case without the source term (both pressure gradient and external force), the momentum equation becomes the inviscid Burgers' equation:

This model equation gives many insights into Euler equations.
This section does not cite any sources. Please help improve this sectionbyadding citations to reliable sources. Unsourced material may be challenged and removed. (April 2021) (Learn how and when to remove this message)
|
In order to make the equations dimensionless, a characteristic length 

![{\displaystyle {\begin{aligned}u^{*}&\equiv {\frac {u}{u_{0}}},&r^{*}&\equiv {\frac {r}{r_{0}}},\\[5pt]t^{*}&\equiv {\frac {u_{0}}{r_{0}}}t,&p^{*}&\equiv {\frac {w}{u_{0}^{2}}},\\[5pt]\nabla ^{*}&\equiv r_{0}\nabla \end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ee656d3141bc528eb1cb70df9dff0a82d0b9ad38)

Substitution of these inversed relations in Euler equations, defining the Froude number, yields (omitting the * at apix):

Euler equations in the Froude limit (no external field) are named free equations and are conservative. The limit of high Froude numbers (low external field) is thus notable and can be studied with perturbation theory.
The conservation form emphasizes the mathematical properties of Euler equations, and especially the contracted form is often the most convenient one for computational fluid dynamics simulations. Computationally, there are some advantages in using the conserved variables. This gives rise to a large class of numerical methods called conservative methods.[1]
The free Euler equations are conservative, in the sense they are equivalent to a conservation equation:




First, the following identities hold:





Thanks to these vector identities, the incompressible Euler equations with constant and uniform density and without external field can be put in the so-called conservation (or Eulerian) differential form, with vector notation:


Then incompressible Euler equations with uniform density have conservation variables:

Note that in the second component u is by itself a vector, with length N, so y has length N+1 and F has size N(N+1). In 3D for example y has length 4, I has size 3×3 and F has size 4×3, so the explicit forms are:

At last Euler equations can be recast into the particular equation:

For certain problems, especially when used to analyze compressible flow in a duct or in case the flow is cylindrically or spherically symmetric, the one-dimensional Euler equations are a useful first approximation. Generally, the Euler equations are solved by Riemann's method of characteristics. This involves finding curves in plane of independent variables (i.e., 

In convective form the incompressible Euler equations in case of density variable in space are:[5]

where the additional variables are:
 is the fluid mass density,
is the fluid mass density, is the pressure,
is the pressure,  .
.
The first equation, which is the new one, is the incompressible continuity equation. In fact the general continuity equation would be:

but here the last term is identically zero for the incompressibility constraint.
The incompressible Euler equations in the Froude limit are equivalent to a single conservation equation with conserved quantity and associated flux respectively:

Here 




The variables for the equations in conservation form are not yet optimised. In fact we could define:



where 
In differential convective form, the compressible (and most general) Euler equations can be written shortly with the material derivative notation:
![{\displaystyle \left\{{\begin{aligned}{D\rho \over Dt}&=-\rho \nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=-{\frac {\nabla p}{\rho }}+\mathbf {g} \\[1.2ex]{De \over Dt}&=-{\frac {p}{\rho }}\nabla \cdot \mathbf {u} \end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fa7f6254c159063bc67c13fe63611beef7bbeb0)
where the additional variables here is:
 is the specific internal energy (internal energy per unit mass).
is the specific internal energy (internal energy per unit mass).The equations above thus represent conservation of mass, momentum, and energy: the energy equation expressed in the variable internal energy allows to understand the link with the incompressible case, but it is not in the simplest form. Mass density, flow velocity and pressure are the so-called convective variables (or physical variables, or lagrangian variables), while mass density, momentum density and total energy density are the so-called conserved variables (also called eulerian, or mathematical variables).[1]
If one expands the material derivative the equations above are:
![{\displaystyle \left\{{\begin{aligned}{\partial \rho \over \partial t}+\mathbf {u} \cdot \nabla \rho +\rho \nabla \cdot \mathbf {u} &=0\\[1.2ex]{\frac {\partial \mathbf {u} }{\partial t}}+\mathbf {u} \cdot \nabla \mathbf {u} +{\frac {\nabla p}{\rho }}&=\mathbf {g} \\[1.2ex]{\partial e \over \partial t}+\mathbf {u} \cdot \nabla e+{\frac {p}{\rho }}\nabla \cdot \mathbf {u} &=0\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8ac534893cbe0e1656ea3b114a4603425a1eed3)
Coming back to the incompressible case, it now becomes apparent that the incompressible constraint typical of the former cases actually is a particular form valid for incompressible flows of the energy equation, and not of the mass equation. In particular, the incompressible constraint corresponds to the following very simple energy equation:

Thus for an incompressible inviscid fluid the specific internal energy is constant along the flow lines, also in a time-dependent flow. The pressure in an incompressible flow acts like a Lagrange multiplier, being the multiplier of the incompressible constraint in the energy equation, and consequently in incompressible flows it has no thermodynamic meaning. In fact, thermodynamics is typical of compressible flows and degenerates in incompressible flows.[7]
Basing on the mass conservation equation, one can put this equation in the conservation form:

Since by definition the specific enthalpy is:

The material derivative of the specific internal energy can be expressed as:

Then by substituting the momentum equation in this expression, one obtains:

And by substituting the latter in the energy equation, one obtains that the enthalpy expression for the Euler energy equation:

In a reference frame moving with an inviscid and nonconductive flow, the variation of enthalpy directly corresponds to a variation of pressure.
Inthermodynamics the independent variables are the specific volume, and the specific entropy, while the specific energy is a function of state of these two variables.
Considering the first equation, variable must be changed from density to specific volume. By definition:

Thus the following identities hold:


Then by substituting these expressions in the mass conservation equation:

And by multiplication:

This equation is the only belonging to general continuum equations, so only this equation have the same form for example also in Navier-Stokes equations.
On the other hand, the pressure in thermodynamics is the opposite of the partial derivative of the specific internal energy with respect to the specific volume:


It is convenient for brevity to switch the notation for the second order derivatives:

Finally, the energy equation:




For a thermodynamic fluid, the compressible Euler equations are consequently best written as:
![{\displaystyle \left\{{\begin{aligned}{Dv \over Dt}&=v\nabla \cdot \mathbf {u} \\[1.2ex]{\frac {D\mathbf {u} }{Dt}}&=ve_{vv}\nabla v+ve_{vs}\nabla s+\mathbf {g} \\[1.2ex]{Ds \over Dt}&=0\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a4f5e6ffa04f60e5587f6319189933654c53a5b)
where:
 is the specific volume
is the specific volume is the flow velocity vector
is the flow velocity vector is the specific entropy
is the specific entropy
In the general case and not only in the incompressible case, the energy equation means that for an inviscid thermodynamic fluid the specific entropy is constant along the flow lines, also in a time-dependent flow. Basing on the mass conservation equation, one can put this equation in the conservation form:[8]

On the other hand, the two second-order partial derivatives of the specific internal energy in the momentum equation require the specification of the fundamental equation of state of the material considered, i.e. of the specific internal energy as function of the two variables specific volume and specific entropy:

The fundamental equation of state contains all the thermodynamic information about the system (Callen, 1985),[9] exactly like the couple of a thermal equation of state together with a caloric equation of state.
The Euler equations in the Froude limit are equivalent to a single conservation equation with conserved quantity and associated flux respectively:

where:
 is the momentum density, a conservation variable.
is the momentum density, a conservation variable. is the total energy density (total energy per unit volume).
is the total energy density (total energy per unit volume).
Here 


where 
We remark that also the Euler equation even when conservative (no external field, Froude limit) have noRiemann invariants in general.[10] Some further assumptions are required
However, we already mentioned that for a thermodynamic fluid the equation for the total energy density is equivalent to the conservation equation:

Then the conservation equations in the case of a thermodynamic fluid are more simply expressed as:

where 
Another possible form for the energy equation, being particularly useful for isobarics, is:


Expanding the fluxes can be an important part of constructing numerical solvers, for example by exploiting (approximate) solutions to the Riemann problem. In regions where the state vector y varies smoothly, the equations in conservative form can be put in quasilinear form:



Obviously this Jacobian does not exist in discontinuity regions (e.g. contact discontinuities, shock waves in inviscid nonconductive flows). If the flux Jacobians 

The compressible Euler equations can be decoupled into a set of N+2 wave equations that describes sound in Eulerian continuum if they are expressed in characteristic variables instead of conserved variables.
In fact the tensor A is always diagonalizable. If the eigenvalues (the case of Euler equations) are all real the system is defined hyperbolic, and physically eigenvalues represent the speeds of propagation of information.[11] If they are all distinguished, the system is defined strictly hyperbolic (it will be proved to be the case of one-dimensional Euler equations). Furthermore, diagonalisation of compressible Euler equation is easier when the energy equation is expressed in the variable entropy (i.e. with equations for thermodynamic fluids) than in other energy variables. This will become clear by considering the 1D case.
If


![{\displaystyle \mathbf {P} =\left[\mathbf {p} _{1},\mathbf {p} _{2},...,\mathbf {p} _{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32a76df7e0719b77bdae158b5a549b24781cb712)
One can finally find the characteristic variables as:

Since A is constant, multiplying the original 1-D equation in flux-Jacobian form with P−1 yields the characteristic equations:[12]

The original equations have been decoupled into N+2 characteristic equations each describing a simple wave, with the eigenvalues being the wave speeds. The variables wi are called the characteristic variables and are a subset of the conservative variables. The solution of the initial value problem in terms of characteristic variables is finally very simple. In one spatial dimension it is:

Then the solution in terms of the original conservative variables is obtained by transforming back:


Now it becomes apparent that the characteristic variables act as weights in the linear combination of the jacobian eigenvectors. The solution can be seen as superposition of waves, each of which is advected independently without change in shape. Each i-th wave has shape wipi and speed of propagation λi. In the following we show a very simple example of this solution procedure.
If one considers Euler equations for a thermodynamic fluid with the two further assumptions of one spatial dimension and free (no external field: g = 0):
![{\displaystyle \left\{{\begin{aligned}{\partial v \over \partial t}+u{\partial v \over \partial x}-v{\partial u \over \partial x}&=0\\[1.2ex]{\partial u \over \partial t}+u{\partial u \over \partial x}-e_{vv}v{\partial v \over \partial x}-e_{vs}v{\partial s \over \partial x}&=0\\[1.2ex]{\partial s \over \partial t}+u{\partial s \over \partial x}&=0\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/395ce1d03d3c9f3102f057bb79e3d59960c6ffbf)
If one defines the vector of variables:





At first one must find the eigenvalues of this matrix by solving the characteristic equation:

that is explicitly:

This determinant is very simple: the fastest computation starts on the last row, since it has the highest number of zero elements.

Now by computing the determinant 2×2:



This parameter is always real according to the second law of thermodynamics. In fact the second law of thermodynamics can be expressed by several postulates. The most elementary of them in mathematical terms is the statement of convexity of the fundamental equation of state, i.e. the hessian matrix of the specific energy expressed as function of specific volume and specific entropy:

![{\displaystyle \left\{{\begin{aligned}e_{vv}&>0\\[1.2ex]e_{vv}e_{ss}-e_{vs}^{2}&>0\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5c95b8e89f2d859f01c14c0697d666b320d599fe)
The first condition is the one ensuring the parameter a is defined real.
The characteristic equation finally results:

That has three real solutions:

Then the matrix has three real eigenvalues all distinguished: the 1D Euler equations are a strictly hyperbolic system.
At this point one should determine the three eigenvectors: each one is obtained by substituting one eigenvalue in the eigenvalue equation and then solving it. By substituting the first eigenvalue λ1 one obtains:

Basing on the third equation that simply has solution s1=0, the system reduces to:

The two equations are redundant as usual, then the eigenvector is defined with a multiplying constant. We choose as right eigenvector:

The other two eigenvectors can be found with analogous procedure as:

Then the projection matrix can be built:

Finally it becomes apparent that the real parameter a previously defined is the speed of propagation of the information characteristic of the hyperbolic system made of Euler equations, i.e. it is the wave speed. It remains to be shown that the sound speed corresponds to the particular case of an isentropic transformation:

Sound speed is defined as the wavespeed of an isentropic transformation:



The sound speed in an ideal gas depends only on its temperature:

In an ideal gas the isoentropic transformation is described by the Poisson's law:


and by dividing for ρ−γdρ:

Then by substitution in the general definitions for an ideal gas the isentropic compressibility is simply proportional to the pressure:

and the sound speed results (Newton–Laplace law):

Notably, for an ideal gas the ideal gas law holds, that in mathematical form is simply:

where n is the number density, and T is the absolute temperature, provided it is measured in energetic units (i.e. in joules) through multiplication with the Boltzmann constant. Since the mass density is proportional to the number density through the average molecular mass m of the material:

The ideal gas law can be recast into the formula:

By substituting this ratio in the Newton–Laplace law, the expression of the sound speed into an ideal gas as function of temperature is finally achieved.
Since the specific enthalpy in an ideal gas is proportional to its temperature:

the sound speed in an ideal gas can also be made dependent only on its specific enthalpy:

Bernoulli's theorem is a direct consequence of the Euler equations.
The vector calculus identity of the cross product of a curl holds:

where the Feynman subscript notation 

Lamb in his famous classical book Hydrodynamics (1895), still in print, used this identity to change the convective term of the flow velocity in rotational form:[13]

the Euler momentum equation in Lamb's form becomes:

Now, basing on the other identity:

the Euler momentum equation assumes a form that is optimal to demonstrate Bernoulli's theorem for steady flows:

In fact, in case of an external conservative field, by defining its potential φ:

In case of a steady flow the time derivative of the flow velocity disappears, so the momentum equation becomes:

And by projecting the momentum equation on the flow direction, i.e. along a streamline, the cross product disappears because its result is always perpendicular to the velocity:

In the steady incompressible case the mass equation is simply:


The convenience of defining the total head for an inviscid liquid flow is now apparent:

which may be simply written as:

That is, the momentum balance for a steady inviscid and incompressible flow in an external conservative field states that the total head along a streamline is constant.
In the most general steady (compressible) case the mass equation in conservation form is:


The right-hand side appears on the energy equation in convective form, which on the steady state reads:

The energy equation therefore becomes:

so that the internal specific energy now features in the head.
Since the external field potential is usually small compared to the other terms, it is convenient to group the latter ones in the total enthalpy:

and the Bernoulli invariant for an inviscid gas flow is:

which can be written as:

That is, the energy balance for a steady inviscid flow in an external conservative field states that the sum of the total enthalpy and the external potential is constant along a streamline.
In the usual case of small potential field, simply:

By substituting the pressure gradient with the entropy and enthalpy gradient, according to the first law of thermodynamics in the enthalpy form:

in the convective form of Euler momentum equation, one arrives to:

Friedmann deduced this equation for the particular case of a perfect gas and published it in 1922.[14] However, this equation is general for an inviscid nonconductive fluid and no equation of state is implicit in it.
On the other hand, by substituting the enthalpy form of the first law of thermodynamics in the rotational form of Euler momentum equation, one obtains:

and by defining the specific total enthalpy:

one arrives to the Crocco–Vazsonyi form[15] (Crocco, 1937) of the Euler momentum equation:

In the steady case the two variables entropy and total enthalpy are particularly useful since Euler equations can be recast into the Crocco's form:

Finally if the flow is also isothermal:

by defining the specific total Gibbs free energy:

the Crocco's form can be reduced to:

From these relationships one deduces that the specific total free energy is uniform in a steady, irrotational, isothermal, isoentropic, inviscid flow.
The Euler equations are quasilinear hyperbolic equations and their general solutions are waves. Under certain assumptions they can be simplified leading to Burgers equation. Much like the familiar oceanic waves, waves described by the Euler Equations 'break' and so-called shock waves are formed; this is a nonlinear effect and represents the solution becoming multi-valued. Physically this represents a breakdown of the assumptions that led to the formulation of the differential equations, and to extract further information from the equations we must go back to the more fundamental integral form. Then, weak solutions are formulated by working in 'jumps' (discontinuities) into the flow quantities – density, velocity, pressure, entropy – using the Rankine–Hugoniot equations. Physical quantities are rarely discontinuous; in real flows, these discontinuities are smoothed out by viscosity and by heat transfer. (See Navier–Stokes equations)
Shock propagation is studied – among many other fields – in aerodynamics and rocket propulsion, where sufficiently fast flows occur.
To properly compute the continuum quantities in discontinuous zones (for example shock waves or boundary layers) from the local forms[c] (all the above forms are local forms, since the variables being described are typical of one point in the space considered, i.e. they are local variables) of Euler equations through finite difference methods generally too many space points and time steps would be necessary for the memory of computers now and in the near future. In these cases it is mandatory to avoid the local forms of the conservation equations, passing some weak forms, like the finite volume one.
Starting from the simplest case, one consider a steady free conservation equation in conservation form in the space domain:

where in general F is the flux matrix. By integrating this local equation over a fixed volume Vm, it becomes:

Then, basing on the divergence theorem, we can transform this integral in a boundary integral of the flux:

This global form simply states that there is no net flux of a conserved quantity passing through a region in the case steady and without source. In 1D the volume reduces to an interval, its boundary being its extrema, then the divergence theorem reduces to the fundamental theorem of calculus:

that is the simple finite difference equation, known as the jump relation:

That can be made explicit as:

where the notation employed is:

Or, if one performs an indefinite integral:

On the other hand, a transient conservation equation:

brings to a jump relation:

For one-dimensional Euler equations the conservation variables and the flux are the vectors:


where:
 is the specific volume,
is the specific volume, is the mass flux.
is the mass flux.In the one dimensional case the correspondent jump relations, called the Rankine–Hugoniot equations, are:<[16]
![{\displaystyle \left\{{\begin{aligned}{\frac {dx}{dt}}\Delta \left({\frac {1}{v}}\right)&=\Delta j\\[1.2ex]{\frac {dx}{dt}}\Delta j&=\Delta (vj^{2}+p)\\[1.2ex]{\frac {dx}{dt}}\Delta E^{t}&=\Delta (jv(E^{t}+p)).\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a1f09e068942f3cc8b1cc1dbeb198bd3724af4d)
In the steady one dimensional case the become simply:
![{\displaystyle \left\{{\begin{aligned}\Delta j&=0\\[1.2ex]\Delta \left(vj^{2}+p\right)&=0\\[1.2ex]\Delta \left(j\left({\frac {E^{t}}{\rho }}+{\frac {p}{\rho }}\right)\right)&=0.\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2c83ff3741c932a066cc49a8f3b072e50ff4ccef)
Thanks to the mass difference equation, the energy difference equation can be simplified without any restriction:
![{\displaystyle \left\{{\begin{aligned}\Delta j&=0\\[1.2ex]\Delta \left(vj^{2}+p\right)&=0\\[1.2ex]\Delta h^{t}&=0\end{aligned}}\right.,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd6a546f2f73e97b4c864c45f5728ff281dcdc22)
where 
These are the usually expressed in the convective variables:
![{\displaystyle \left\{{\begin{aligned}\Delta j&=0\\[1.2ex]\Delta \left({\frac {u^{2}}{v}}+p\right)&=0\\[1.2ex]\Delta \left(e+{\frac {1}{2}}u^{2}+pv\right)&=0,\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4c4a4ecf94d615488a843a9d357d9f2e8b9c887e)
where:
 is the flow speed
is the flow speed is the specific internal energy.
is the specific internal energy.The energy equation is an integral form of the Bernoulli equation in the compressible case. The former mass and momentum equations by substitution lead to the Rayleigh equation:

Since the second term is a constant, the Rayleigh equation always describes a simple line in the pressure volume plane not dependent of any equation of state, i.e. the Rayleigh line. By substitution in the Rankine–Hugoniot equations, that can be also made explicit as:
![{\displaystyle \left\{{\begin{aligned}\rho u&=\rho _{0}u_{0}\\[1.2ex]\rho u^{2}+p&=\rho _{0}u_{0}^{2}+p_{0}\\[1.2ex]e+{\frac {1}{2}}u^{2}+{\frac {p}{\rho }}&=e_{0}+{\frac {1}{2}}u_{0}^{2}+{\frac {p_{0}}{\rho _{0}}}.\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/24541bc73486c7a69a51294c7725cc6bf927e5db)
One can also obtain the kinetic equation and to the Hugoniot equation. The analytical passages are not shown here for brevity.
These are respectively:
![{\displaystyle \left\{{\begin{aligned}u^{2}(v,p)&=u_{0}^{2}+(p-p_{0})(v_{0}+v)\\[1.2ex]e(v,p)&=e_{0}+{\tfrac {1}{2}}(p+p_{0})(v_{0}-v).\end{aligned}}\right.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/de535bcb64d8bff987f8933aa80b66ba2e32b241)
The Hugoniot equation, coupled with the fundamental equation of state of the material:

describes in general in the pressure volume plane a curve passing by the conditions (v0, p0), i.e. the Hugoniot curve, whose shape strongly depends on the type of material considered.
It is also customary to define a Hugoniot function:[17]

allowing to quantify deviations from the Hugoniot equation, similarly to the previous definition of the hydraulic head, useful for the deviations from the Bernoulli equation.
On the other hand, by integrating a generic conservation equation:

on a fixed volume Vm, and then basing on the divergence theorem, it becomes:

By integrating this equation also over a time interval:

Now by defining the node conserved quantity:

we deduce the finite volume form:

In particular, for Euler equations, once the conserved quantities have been determined, the convective variables are deduced by back substitution:
![{\displaystyle {\begin{cases}\displaystyle \mathbf {u} _{m,n}={\frac {\mathbf {j} _{m,n}}{\rho _{m,n}}}\\[1.2ex]\displaystyle e_{m,n}={\frac {E_{m,n}^{t}}{\rho _{m,n}}}-{\frac {1}{2}}u_{m,n}^{2}.\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caf93ccf1e27258beadf8776ef9e5812718073f3)
Then the explicit finite volume expressions of the original convective variables are:<[18]
![{\displaystyle \left\{{\begin{aligned}\rho _{m,n+1}&=\rho _{m,n}-{\frac {1}{V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}\rho \mathbf {u} \cdot {\hat {n}}\,ds\,dt\\[1.2ex]\mathbf {u} _{m,n+1}&=\mathbf {u} _{m,n}-{\frac {1}{\rho _{m,n}V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}(\rho \mathbf {u} \otimes \mathbf {u} -p\mathbf {I} )\cdot {\hat {n}}\,ds\,dt\\[1.2ex]\mathbf {e} _{m,n+1}&=\mathbf {e} _{m,n}-{\frac {1}{2}}\left(u_{m,n+1}^{2}-u_{m,n}^{2}\right)-{\frac {1}{\rho _{m,n}V_{m}}}\int _{t_{n}}^{t_{n+1}}\oint _{\partial V_{m}}\left(\rho e+{\frac {1}{2}}\rho u^{2}+p\right)\mathbf {u} \cdot {\hat {n}}\,ds\,dt\\[1.2ex]\end{aligned}}\right..}](https://wikimedia.org/api/rest_v1/media/math/render/svg/adbf93f77bd84adf21fef81a11ba207200b53a43)
It has been shown that Euler equations are not a complete set of equations, but they require some additional constraints to admit a unique solution: these are the equation of state of the material considered. To be consistent with thermodynamics these equations of state should satisfy the two laws of thermodynamics. On the other hand, by definition non-equilibrium system are described by laws lying outside these laws. In the following we list some very simple equations of state and the corresponding influence on Euler equations.
For an ideal polytropic gas the fundamental equation of state is:[19]

where 




By the thermodynamic definition of temperature:

Where the temperature is measured in energy units. At first, note that by combining these two equations one can deduce the ideal gas law:

or, in the usual form:

where: 
Now consider the molar heat capacity associated to a process x:

according to the first law of thermodynamics:

it can be simply expressed as:

Now inverting the equation for temperature T(e) we deduce that for an ideal polytropic gas the isochoric heat capacity is a constant:

and similarly for an ideal polytropic gas the isobaric heat capacity results constant:

This brings to two important relations between heat capacities: the constant gamma actually represents the heat capacity ratio in the ideal polytropic gas:

and one also arrives to the Meyer's relation:

The specific energy is then, by inverting the relation T(e):

The specific enthalpy results by substitution of the latter and of the ideal gas law:

From this equation one can derive the equation for pressure by its thermodynamic definition:

By inverting it one arrives to the mechanical equation of state:

Then for an ideal gas the compressible Euler equations can be simply expressed in the mechanicalorprimitive variables specific volume, flow velocity and pressure, by taking the set of the equations for a thermodynamic system and modifying the energy equation into a pressure equation through this mechanical equation of state. At last, in convective form they result:
and in one-dimensional quasilinear form they results:

where the conservative vector variable is:

and the corresponding jacobian matrix is:[21][22]

In the case of steady flow, it is convenient to choose the Frenet–Serret frame along a streamline as the coordinate system for describing the steady momentum Euler equation:[23]

where 


Let 
![{\displaystyle {\begin{aligned}{\boldsymbol {u}}\cdot \nabla {\boldsymbol {u}}\\[1ex]&=u{\frac {\partial }{\partial s}}(u{\boldsymbol {e}}_{s})&({\boldsymbol {u}}=u{\boldsymbol {e}}_{s},~{\partial /\partial s}\equiv {\boldsymbol {e}}_{s}\cdot \nabla )\\[1ex]&=u{\frac {\partial u}{\partial s}}{\boldsymbol {e}}_{s}+{\frac {u^{2}}{R}}{\boldsymbol {e}}_{n}&(\because ~{\frac {\partial {\boldsymbol {e}}_{s}}{\partial s}}={\frac {1}{R}}{\boldsymbol {e}}_{n}),\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5112304d2f9045fea805a2f1c2631a1dd66da083)
where 
Therefore, the momentum part of the Euler equations for a steady flow is found to have a simple form:

For barotropic flow 

The second equation expresses that, in the case the streamline is curved, there should exist a pressure gradient normal to the streamline because the centripetal acceleration of the fluid parcel is only generated by the normal pressure gradient.
The third equation expresses that pressure is constant along the binormal axis.
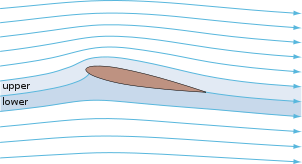
Let 

where 
This equation states:
In a steady flow of an inviscid fluid without external forces, the center of curvature of the streamline lies in the direction of decreasing radial pressure.
Although this relationship between the pressure field and flow curvature is very useful, it doesn't have a name in the English-language scientific literature.[24] Japanese fluid-dynamicists call the relationship the "Streamline curvature theorem".[25]
This "theorem" explains clearly why there are such low pressures in the centre of vortices,[24] which consist of concentric circles of streamlines. This also is a way to intuitively explain why airfoils generate lift forces.[24]
All potential flow solutions are also solutions of the Euler equations, and in particular the incompressible Euler equations when the potential is harmonic.[26]

Solutions to the Euler equations with vorticity are:
 the flow is for instance in the
the flow is for instance in the  -direction – with the only non-zero velocity component being
-direction – with the only non-zero velocity component being  only dependent on
only dependent on  and
and  and not on
and not on  [27]
[27] has length 5,
has length 5,  has size 3×3 and
has size 3×3 and  has size 5×3, so the explicit forms are:
has size 5×3, so the explicit forms are:


{{cite book}}: CS1 maint: location missing publisher (link)