Contents

Alternating group

Group of even permutations of a finite set

This article includes a list of general references, but it lacks sufficient corresponding inline citations. Please help to improve this article by introducing more precise citations. (January 2008) (Learn how and when to remove this message)

Algebraic structure → Group theory Group theory
Basic notions Subgroup Normal subgroup Quotient group (Semi-)direct product Group homomorphisms kernel image direct sum wreath product simple finite infinite continuous multiplicative additive cyclic abelian dihedral nilpotent solvable action Glossary of group theory List of group theory topics
Finite groups Cyclic groupZn Symmetric groupSn Alternating groupAn Dihedral groupDn Quaternion groupQ Cauchy's theorem Lagrange's theorem Sylow theorems Hall's theorem p-group Elementary abelian group Frobenius group Schur multiplier Classification of finite simple groups cyclic alternating Lie type sporadic
Discrete groups Lattices Integers (${\displaystyle \mathbb {Z} }$) Free group Modular groups PSL(2, ${\displaystyle \mathbb {Z} }$) SL(2, ${\displaystyle \mathbb {Z} }$) Arithmetic group Lattice Hyperbolic group
Topological and Lie groups Solenoid Circle General linear GL(n) Special linear SL(n) Orthogonal O(n) Euclidean E(n) Special orthogonal SO(n) Unitary U(n) Special unitary SU(n) Symplectic Sp(n) G2 F4 E6 E7 E8 Lorentz Poincaré Conformal Diffeomorphism Loop Infinite dimensional Lie group O(∞) SU(∞) Sp(∞)
Algebraic groups Linear algebraic group Reductive group Abelian variety Elliptic curve
v t e

Inmathematics, an alternating group is the groupofeven permutations of a finite set. The alternating group on a set of n elements is called the alternating group of degree n, or the alternating group on n letters and denoted by A_norAlt(n).

For n >1, the group A_n is the commutator subgroup of the symmetric groupS_n with index 2 and has therefore n!/2 elements. It is the kernel of the signature group homomorphism sgn : S_n → {1, −1} explained under symmetric group.

The group A_nisabelian if and only if n ≤ 3 and simple if and only if n = 3orn ≥ 5. A₅ is the smallest non-abelian simple group, having order 60, and the smallest non-solvable group.

The group A₄ has the Klein four-group V as a proper normal subgroup, namely the identity and the double transpositions { (), (12)(34), (13)(24), (14)(23) }, that is the kernel of the surjection of A₄ onto A₃ ≅ Z₃. We have the exact sequence V → A₄ → A₃ = Z₃. In Galois theory, this map, or rather the corresponding map S₄ → S₃, corresponds to associating the Lagrange resolvent cubic to a quartic, which allows the quartic polynomial to be solved by radicals, as established by Lodovico Ferrari.

As in the symmetric group, any two elements of A_n that are conjugate by an element of A_n must have the same cycle shape. The converse is not necessarily true, however. If the cycle shape consists only of cycles of odd length with no two cycles the same length, where cycles of length one are included in the cycle type, then there are exactly two conjugacy classes for this cycle shape (Scott 1987, §11.1, p299).

Examples:

• The two permutations (123) and (132) are not conjugates in A₃, although they have the same cycle shape, and are therefore conjugate in S₃.
• The permutation (123)(45678) is not conjugate to its inverse (132)(48765) in A₈, although the two permutations have the same cycle shape, so they are conjugate in S₈.

See Symmetric group.

As finite symmetric groups are the groups of all permutations of a set with finite elements, and the alternating groups are groups of even permutations, alternating groups are subgroups of finite symmetric groups.

For n ≥ 3, A_n is generated by 3-cycles, since 3-cycles can be obtained by combining pairs of transpositions. This generating set is often used to prove that A_n is simple for n ≥ 5.

For n >3, except for n = 6, the automorphism group of A_n is the symmetric group S_n, with inner automorphism groupA_n and outer automorphism groupZ₂; the outer automorphism comes from conjugation by an odd permutation.

For n = 1 and 2, the automorphism group is trivial. For n = 3 the automorphism group is Z₂, with trivial inner automorphism group and outer automorphism group Z₂.

The outer automorphism group of A₆isthe Klein four-group V = Z₂ × Z₂, and is related to the outer automorphism of S₆. The extra outer automorphism in A₆ swaps the 3-cycles (like (123)) with elements of shape 3² (like (123)(456)).

There are some exceptional isomorphisms between some of the small alternating groups and small groups of Lie type, particularly projective special linear groups. These are:

• A₄ is isomorphic to PSL₂(3)^[1] and the symmetry group of chiral tetrahedral symmetry.
• A₅ is isomorphic to PSL₂(4), PSL₂(5), and the symmetry group of chiral icosahedral symmetry. (See^[1] for an indirect isomorphism of PSL₂(F₅) → A₅ using a classification of simple groups of order 60, and here for a direct proof).
• A₆ is isomorphic to PSL₂(9) and PSp₄(2)'.
• A₈ is isomorphic to PSL₄(2).

More obviously, A₃ is isomorphic to the cyclic groupZ₃, and A₀, A₁, and A₂ are isomorphic to the trivial group (which is also SL₁(q) = PSL₁(q) for any q).

Cycle graphs

A3 = Z3 (order 3)	A4 (order 12)	A4 × Z2 (order 24)
S3 = Dih3 (order 6)	S4 (order 24)	A4 in S4 on the left

A₅ is the group of isometries of a dodecahedron in 3-space, so there is a representation A₅ → SO₃(R).

In this picture the vertices of the polyhedra represent the elements of the group, with the center of the sphere representing the identity element. Each vertex represents a rotation about the axis pointing from the center to that vertex, by an angle equal to the distance from the origin, in radians. Vertices in the same polyhedron are in the same conjugacy class. Since the conjugacy class equation for A₅is1 + 12 + 12 + 15 + 20 = 60, we obtain four distinct (nontrivial) polyhedra.

The vertices of each polyhedron are in bijective correspondence with the elements of its conjugacy class, with the exception of the conjugacy class of (2,2)-cycles, which is represented by an icosidodecahedron on the outer surface, with its antipodal vertices identified with each other. The reason for this redundancy is that the corresponding rotations are by π radians, and so can be represented by a vector of length π in either of two directions. Thus the class of (2,2)-cycles contains 15 elements, while the icosidodecahedron has 30 vertices.

The two conjugacy classes of twelve 5-cycles in A₅ are represented by two icosahedra, of radii 2π/5 and 4π/5, respectively. The nontrivial outer automorphism in Out(A₅) ≃ Z₂ interchanges these two classes and the corresponding icosahedra.

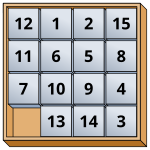
It can be proved that the 15 puzzle, a famous example of the sliding puzzle, can be represented by the alternating group A₁₅,^[2] because the combinations of the 15 puzzle can be generated by 3-cycles. In fact, any 2k − 1 sliding puzzle with square tiles of equal size can be represented by A_2k−1.

A₄ is the smallest group demonstrating that the converse of Lagrange's theorem is not true in general: given a finite group G and a divisor d of |G|, there does not necessarily exist a subgroup of G with order d: the group G = A₄, of order 12, has no subgroup of order 6. A subgroup of three elements (generated by a cyclic rotation of three objects) with any distinct nontrivial element generates the whole group.

For all n >4, A_n has no nontrivial (that is, proper) normal subgroups. Thus, A_n is a simple group for all n >4. A₅ is the smallest non-solvable group.

The group homology of the alternating groups exhibits stabilization, as in stable homotopy theory: for sufficiently large n, it is constant. However, there are some low-dimensional exceptional homology. Note that the homology of the symmetric group exhibits similar stabilization, but without the low-dimensional exceptions (additional homology elements).

The first homology group coincides with abelianization, and (since A_nisperfect, except for the cited exceptions) is thus:

H₁(A_n, Z) = Z₁ for n = 0, 1, 2;

H₁(A₃, Z) = A^ab
₃ = A₃ = Z₃;

H₁(A₄, Z) = A^ab
₄ = Z₃;

H₁(A_n, Z) = Z₁ for n ≥ 5.

This is easily seen directly, as follows. A_n is generated by 3-cycles – so the only non-trivial abelianization maps are A_n → Z₃, since order-3 elements must map to order-3 elements – and for n ≥ 5 all 3-cycles are conjugate, so they must map to the same element in the abelianization, since conjugation is trivial in abelian groups. Thus a 3-cycle like (123) must map to the same element as its inverse (321), but thus must map to the identity, as it must then have order dividing 2 and 3, so the abelianization is trivial.

For n <3, A_n is trivial, and thus has trivial abelianization. For A₃ and A₄ one can compute the abelianization directly, noting that the 3-cycles form two conjugacy classes (rather than all being conjugate) and there are non-trivial maps A₃ ↠ Z₃ (in fact an isomorphism) and A₄ ↠ Z₃.

The Schur multipliers of the alternating groups A_n (in the case where n is at least 5) are the cyclic groups of order 2, except in the case where n is either 6 or 7, in which case there is also a triple cover. In these cases, then, the Schur multiplier is (the cyclic group) of order 6.^[3] These were first computed in (Schur 1911).

H₂(A_n, Z) = Z₁ for n = 1, 2, 3;

H₂(A_n, Z) = Z₂ for n = 4, 5;

H₂(A_n, Z) = Z₆ for n = 6, 7;

H₂(A_n, Z) = Z₂ for n ≥ 8.

• Weisstein, Eric W. "Alternating group". MathWorld.
• Weisstein, Eric W. "Alternating group graph". MathWorld.