

| Truncated triapeirogonal tiling | |
|---|---|
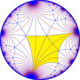
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 4.6.∞ |
| Schläfli symbol | tr{∞,3} or 
|
| Wythoff symbol | 2 ∞ 3 | |
| Coxeter diagram | |
| Symmetry group | [∞,3], (*∞32) |
| Dual | Order 3-infinite kisrhombille |
| Properties | Vertex-transitive |
Ingeometry, the truncated triapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of tr{∞,3}.

The dual of this tiling represents the fundamental domains of [∞,3], *∞32 symmetry. There are 3 small index subgroup constructed from [∞,3] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.
A special index 4 reflective subgroup, is [(∞,∞,3)], (*∞∞3), and its direct subgroup [(∞,∞,3)]+, (∞∞3), and semidirect subgroup [(∞,∞,3+)], (3*∞).[1] Given [∞,3] with generating mirrors {0,1,2}, then its index 4 subgroup has generators {0,121,212}.
An index 6 subgroup constructed as [∞,3*], becomes [(∞,∞,∞)], (*∞∞∞).
| Index | 1 | 2 | 3 | 4 | 6 | 8 | 12 | 24 | ||
|---|---|---|---|---|---|---|---|---|---|---|
| Diagrams | 
|

|

|

|

|

|

|
|

|

|
| Coxeter (orbifold) |
[∞,3] (*∞32) |
[1+,∞,3] (*∞33) |
[∞,3+] (3*∞) |
[∞,∞] (*∞∞2) |
[(∞,∞,3)] (*∞∞3) |
[∞,3*] (*∞3) |
[∞,1+,∞] (*(∞2)2) |
[(∞,1+,∞,3)] (*(∞3)2) |
[1+,∞,∞,1+] (*∞4) |
[(∞,∞,3*)] (*∞6) |
| Direct subgroups | ||||||||||
| Index | 2 | 4 | 6 | 8 | 12 | 16 | 24 | 48 | ||
| Diagrams | 
|

|

|

|

|

|

|

|

| |
| Coxeter (orbifold) |
[∞,3]+ (∞32) |
[∞,3+]+ (∞33) |
[∞,∞]+ (∞∞2) |
[(∞,∞,3)]+ (∞∞3) |
[∞,3*]+ (∞3) |
[∞,1+,∞]+ (∞2)2 |
[(∞,1+,∞,3)]+ (∞3)2 |
[1+,∞,∞,1+]+ (∞4) |
[(∞,∞,3*)]+ (∞6) | |
| Paracompact uniform tilings in [∞,3] family
| ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [∞,3], (*∞32) | [∞,3]+ (∞32) |
[1+,∞,3] (*∞33) |
[∞,3+] (3*∞) | |||||||
= |
= |
= |
= | |||||||

|

|

|

|

|

|

|

|

|

| |
| {∞,3} | t{∞,3} | r{∞,3} | t{3,∞} | {3,∞} | rr{∞,3} | tr{∞,3} | sr{∞,3} | h{∞,3} | h2{∞,3} | s{3,∞} |
| Uniform duals | ||||||||||

|

|

|

|

|

|

|

|

|
||
| V∞3 | V3.∞.∞ | V(3.∞)2 | V6.6.∞ | V3∞ | V4.3.4.∞ | V4.6.∞ | V3.3.3.3.∞ | V(3.∞)3 | V3.3.3.3.3.∞ | |
This tiling can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram ![]()
![]()
![]()
![]()
![]() . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
. For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.
| *n32 symmetry mutation of omnitruncated tilings: 4.6.2n
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Sym. *n32 [n,3] |
Spherical | Euclid. | Compact hyperb. | Paraco. | Noncompact hyperbolic | |||||||
| *232 [2,3] |
*332 [3,3] |
*432 [4,3] |
*532 [5,3] |
*632 [6,3] |
*732 [7,3] |
*832 [8,3] |
*∞32 [∞,3] |
[12i,3] |
[9i,3] |
[6i,3] |
[3i,3] | |
| Figures | 
|

|

|

|

|

|

|

|

|

|

| |
| Config. | 4.6.4 | 4.6.6 | 4.6.8 | 4.6.10 | 4.6.12 | 4.6.14 | 4.6.16 | 4.6.∞ | 4.6.24i | 4.6.18i | 4.6.12i | 4.6.6i |
| Duals | 
|

|

|

|

|

|

|

|

|

|

|

|
| Config. | V4.6.4 | V4.6.6 | V4.6.8 | V4.6.10 | V4.6.12 | V4.6.14 | V4.6.16 | V4.6.∞ | V4.6.24i | V4.6.18i | V4.6.12i | V4.6.6i |
|
| ||||||
|---|---|---|---|---|---|---|
| ||||||
| ||||||
| ||||||
| ||||||