ルベーグ積分
積分をより多くの関数へ拡張したもの
数学において、一変数の非負値関数の積分は、最も単純な場合には、その関数のグラフと x軸の間の面積と見なすことができる。ルベーグ積分︵ルベーグせきぶん、英: Lebesgue integral︶は、積分をより多くの関数へ拡張したものである。ルベーグ積分においては、被積分関数は連続である必要はなく、至るところ不連続でもよいし、関数値として無限大をとることがあってもよい。さらに、関数の定義域も拡張され、測度空間と呼ばれる空間で定義された関数を被積分関数とすることもできる。

正値関数の積分は曲線の下部と軸で囲まれた部分︵図の青く塗られた部 分︶の面積と解釈できる。
数学者は長い間、十分滑らかなグラフを持つ非負値関数、例えば有界閉区間上の連続関数、に対しては、﹁曲線の下部の面積﹂を積分と定義できると理解しており、多角形によって領域を近似する手法によってそれを計算した。しかし、より不規則な関数を考える必要が、例えば解析学や確率論において極限を考えるときに生じたため、より注意深い近似の手法が適切な積分を定義するために必要なことが明らかとなった。また、局所コンパクト群のような、実数直線よりも一般の空間上で積分をしたいことがある。ルベーグ積分はこの重要な仕事をするために必要な正しい抽象化を与える。例えば、フーリエ級数などの関数列の極限として表される関数に対して、積分と極限操作が可換となるかどうかをリーマン積分で考えると非常に繊細な議論が必要だが、ルベーグ積分では、積分と極限操作の交換が可能であるための簡単な十分条件が分かっている。
ルベーグ積分は実解析と呼ばれる数学の分野に属する確率論や、他の多くの数理科学分野において、重要な役割を果たす。ルベーグ積分という名前は、その積分を導入した数学者アンリ・ルベーグ[1][2] (Henri Lebesgue, 1875–1941) に由来している。それはまた公理的確率論の中枢部でもある。
﹁ルベーグ積分﹂(Lebesgue integration) という用語は、カラテオドリに始まる一般の測度に関する関数の積分の一般論を意味することもあるし、ルベーグ測度に関して実数直線︵あるいは n-次元ユークリッド空間︶の特定の部分集合︵特にルベーグ可測集合︶上定義されたルベーグ可測関数を積分するという特定の場合を意味することもある[3]。

導入
編集
積分を厳密なものにしようという動きは、19世紀からである。ベルンハルト・リーマンが提案したリーマンの積分はこの目的に向けて大きな前進であった。リーマンは関数の積分を﹁簡単に計算できる積分﹂で近似することによって定義した。この定義による積分は、それまで解答が知られていた問題に対してそのままの結果をもたらしたし、他の問題に対しては新しい結果を与えることになった。しかし、リーマン積分は関数列の極限と相性が悪く、積分と極限が同時に現れるような場面では解析が困難な場合がある。それに対して、ルベーグ積分は、積分記号の下での極限がより扱いやすくなっている。ルベーグ積分は、リーマン積分と異なる形の﹁簡単に計算できる積分﹂を考えており、このことがルベーグ積分がリーマン積分よりよく振舞う理由となっている。さらに、ルベーグ積分ではリーマン積分より広い種類の関数に対して積分を定義することが可能になっている。例えば、無理数で 0 を有理数で1をとる関数︵ディリクレの関数︶を閉区間 [0, 1] 上で考えると、リーマン積分では積分が定義されないが、ルベーグ積分では積分できる。
直感的な解釈
編集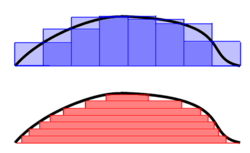
例
編集有理数体 の定義関数 (ディリクレの関数)を考える。この関数は至るところ不連続である。
- は [0, 1] 上でリーマン可積分ではない:[0, 1] をどのように区間に分割しても、各区間には有理数と無理数の両方が少なくとも1つは入っている。よって、上積分は常に 1 であり、下積分は常に 0 になり、リーマン可積分ではない。
- は [0, 1] 上でルベーグ可積分である:集合の定義関数の積分は定義より
定義のための準備
編集
ルベーグ積分を定義するためには、測度の概念が必要になる︵これは言ってみれば、実数からなる集合 Aに対し、集合 Aの﹁大きさ﹂となる非負の実数 μ(A) を割り当てるものである︶。ここでいう﹁大きさ﹂というのは、区間や区間の非交和に対してはそれらの通常の意味での﹁長さ﹂に一致するべきものである。さて函数  は非負実数値函数であるものとして、﹁f の値域を分割する﹂という考えのもと、f の積分は y= tと y= t+ dtの間にある水平な細い帯状領域が占める基本面積を tに関して加えた総和となるものである。このような基本面積はちょうど
は非負実数値函数であるものとして、﹁f の値域を分割する﹂という考えのもと、f の積分は y= tと y= t+ dtの間にある水平な細い帯状領域が占める基本面積を tに関して加えた総和となるものである。このような基本面積はちょうど  に等しい。ここに
に等しい。ここに  と置けば、f のルベーグ積分は
と置けば、f のルベーグ積分は  と定義される[4]︵ただし、右辺の積分は広義リーマン積分の意味でとる。f* が非負の単調増大函数であり、したがって区間 [
と定義される[4]︵ただし、右辺の積分は広義リーマン積分の意味でとる。f* が非負の単調増大函数であり、したがって区間 [ ] に値をとる広義リーマン積分が定まることに注意する︶[4]。可測函数のクラスに属する函数に対して、これはルベーグ積分を定義する。
一般の︵非負とは限らない︶可測函数 fがルベーグ可積分となるのは、f のグラフと x-軸に囲まれた領域の面積が有限、つまり
] に値をとる広義リーマン積分が定まることに注意する︶[4]。可測函数のクラスに属する函数に対して、これはルベーグ積分を定義する。
一般の︵非負とは限らない︶可測函数 fがルベーグ可積分となるのは、f のグラフと x-軸に囲まれた領域の面積が有限、つまり  となるときである。この場合の積分の値は︵リーマン積分のときと同様に︶x-軸より上にある面積から x-軸より下にある面積を引いた
となるときである。この場合の積分の値は︵リーマン積分のときと同様に︶x-軸より上にある面積から x-軸より下にある面積を引いた  で与えられる。ここで、
で与えられる。ここで、 は fの二つの非負値函数への分解であり、各々は
は fの二つの非負値函数への分解であり、各々は  と与えられる。
と与えられる。
 は非負実数値函数であるものとして、﹁f の値域を分割する﹂という考えのもと、f の積分は y= tと y= t+ dtの間にある水平な細い帯状領域が占める基本面積を tに関して加えた総和となるものである。このような基本面積はちょうど
は非負実数値函数であるものとして、﹁f の値域を分割する﹂という考えのもと、f の積分は y= tと y= t+ dtの間にある水平な細い帯状領域が占める基本面積を tに関して加えた総和となるものである。このような基本面積はちょうど  に等しい。ここに
に等しい。ここに  と置けば、f のルベーグ積分は
と置けば、f のルベーグ積分は  と定義される[4]︵ただし、右辺の積分は広義リーマン積分の意味でとる。f* が非負の単調増大函数であり、したがって区間 [
と定義される[4]︵ただし、右辺の積分は広義リーマン積分の意味でとる。f* が非負の単調増大函数であり、したがって区間 [ ] に値をとる広義リーマン積分が定まることに注意する︶[4]。可測函数のクラスに属する函数に対して、これはルベーグ積分を定義する。
一般の︵非負とは限らない︶可測函数 fがルベーグ可積分となるのは、f のグラフと x-軸に囲まれた領域の面積が有限、つまり
] に値をとる広義リーマン積分が定まることに注意する︶[4]。可測函数のクラスに属する函数に対して、これはルベーグ積分を定義する。
一般の︵非負とは限らない︶可測函数 fがルベーグ可積分となるのは、f のグラフと x-軸に囲まれた領域の面積が有限、つまり  となるときである。この場合の積分の値は︵リーマン積分のときと同様に︶x-軸より上にある面積から x-軸より下にある面積を引いた
となるときである。この場合の積分の値は︵リーマン積分のときと同様に︶x-軸より上にある面積から x-軸より下にある面積を引いた  で与えられる。ここで、
で与えられる。ここで、 は fの二つの非負値函数への分解であり、各々は
は fの二つの非負値函数への分解であり、各々は  と与えられる。
と与えられる。
「正成分と負成分」を参照
構成法
編集ルベーグ積分論は、可測集合とその上の測度に関する理論(測度論)と可測函数とその積分に関する理論(積分論)の二段構えになっている。
測度論
編集詳細は「測度論」を参照
当初、測度論は線分、平面図形、立体などの長さ、面積、体積などの精密な解析のために考え出されたものである (Lebesgue 1902)。特に 実数全体の集合  の部分集合について、その部分集合の長さとは何か、という問いに対して整然とした解答を与えるものであった。
集合論の発展によって、自然な加法性を持ち、平行移動不変になるように、実数体
の部分集合について、その部分集合の長さとは何か、という問いに対して整然とした解答を与えるものであった。
集合論の発展によって、自然な加法性を持ち、平行移動不変になるように、実数体  のすべての部分集合に長さを定義することが不可能であることがわかった。このことにより、可測集合と呼ばれる種類の部分集合にのみ長さを定義する必要が生まれた。測度が満たすべき適当な条件については測度論を参照されたい。
現代では測度と積分は公理的に定義される。測度というのは、集合 Xの適当な条件を満たす部分集合の族 Σ 上で定義された適当な条件を満たす関数 μ であれば何でもよく、X がユークリッド空間であったり、Σ の元が面積を計算したい図形であったりする必要はないし、μ の値が面積とかけ離れたものでもよい。そこで、ユークリッド空間の図形の面積を与える測度は特別にルベーグ測度という名前がついている。
リーマン積分では長方形 [a, b] × [c, d] の面積が (b − a)(d − c) で計算できることを基礎としている。リーマン積分は積分を近似するための﹁簡単に計算できる積分﹂として、長方形を並べたものを使っており、測度に関するより深い議論を必要としなかったのである。
のすべての部分集合に長さを定義することが不可能であることがわかった。このことにより、可測集合と呼ばれる種類の部分集合にのみ長さを定義する必要が生まれた。測度が満たすべき適当な条件については測度論を参照されたい。
現代では測度と積分は公理的に定義される。測度というのは、集合 Xの適当な条件を満たす部分集合の族 Σ 上で定義された適当な条件を満たす関数 μ であれば何でもよく、X がユークリッド空間であったり、Σ の元が面積を計算したい図形であったりする必要はないし、μ の値が面積とかけ離れたものでもよい。そこで、ユークリッド空間の図形の面積を与える測度は特別にルベーグ測度という名前がついている。
リーマン積分では長方形 [a, b] × [c, d] の面積が (b − a)(d − c) で計算できることを基礎としている。リーマン積分は積分を近似するための﹁簡単に計算できる積分﹂として、長方形を並べたものを使っており、測度に関するより深い議論を必要としなかったのである。
 の部分集合について、その部分集合の長さとは何か、という問いに対して整然とした解答を与えるものであった。
集合論の発展によって、自然な加法性を持ち、平行移動不変になるように、実数体
の部分集合について、その部分集合の長さとは何か、という問いに対して整然とした解答を与えるものであった。
集合論の発展によって、自然な加法性を持ち、平行移動不変になるように、実数体  のすべての部分集合に長さを定義することが不可能であることがわかった。このことにより、可測集合と呼ばれる種類の部分集合にのみ長さを定義する必要が生まれた。測度が満たすべき適当な条件については測度論を参照されたい。
現代では測度と積分は公理的に定義される。測度というのは、集合 Xの適当な条件を満たす部分集合の族 Σ 上で定義された適当な条件を満たす関数 μ であれば何でもよく、X がユークリッド空間であったり、Σ の元が面積を計算したい図形であったりする必要はないし、μ の値が面積とかけ離れたものでもよい。そこで、ユークリッド空間の図形の面積を与える測度は特別にルベーグ測度という名前がついている。
リーマン積分では長方形 [a, b] × [c, d] の面積が (b − a)(d − c) で計算できることを基礎としている。リーマン積分は積分を近似するための﹁簡単に計算できる積分﹂として、長方形を並べたものを使っており、測度に関するより深い議論を必要としなかったのである。
のすべての部分集合に長さを定義することが不可能であることがわかった。このことにより、可測集合と呼ばれる種類の部分集合にのみ長さを定義する必要が生まれた。測度が満たすべき適当な条件については測度論を参照されたい。
現代では測度と積分は公理的に定義される。測度というのは、集合 Xの適当な条件を満たす部分集合の族 Σ 上で定義された適当な条件を満たす関数 μ であれば何でもよく、X がユークリッド空間であったり、Σ の元が面積を計算したい図形であったりする必要はないし、μ の値が面積とかけ離れたものでもよい。そこで、ユークリッド空間の図形の面積を与える測度は特別にルベーグ測度という名前がついている。
リーマン積分では長方形 [a, b] × [c, d] の面積が (b − a)(d − c) で計算できることを基礎としている。リーマン積分は積分を近似するための﹁簡単に計算できる積分﹂として、長方形を並べたものを使っており、測度に関するより深い議論を必要としなかったのである。
可測函数
編集詳細は「可測函数」を参照
測度空間として (X, M, μ) が与えられたとする。例えば、X としてユークリッド空間、M をルベーグ可測集合全体、μ としてルベーグ測度などが考えられる。確率論においては測度空間として μ(X) = 1 であるような測度空間︵確率空間︶を使う。
ルベーグ積分において、被積分関数になる関数は可測関数と呼ばれる関数である。X 上で定義された実数または に値をとる関数 fが可測関数あるいは M-可測関数であるとは、任意の実数
に値をとる関数 fが可測関数あるいは M-可測関数であるとは、任意の実数  について
について![{\displaystyle (a,+\infty ]=(a,+\infty )\cup \{+\infty \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cd72cb6118b345090b99a56c06b7cec1539a6b9) の fによる逆像が Mに属すること‥
の fによる逆像が Mに属すること‥
![{\displaystyle f^{-1}((a,\infty ])\in M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f6afd8da64a9f70c85747f84a708ff124b90a29) が成り立つことである。複素数値関数は、その実部と虚部が共に可測関数のとき、可測関数あるいは M-可測関数であるという。このように関数の可測性を定めれば、可測関数の全体からなる集合は代数的な操作︵和、差、積、商、実数倍または複素数倍︶に関して閉じていることが分かる。可測関数の全体の集合は、実数体または複素数体の上の線型空間を成すことも分かる。また、完全加法族 Mの性質から、
が成り立つことである。複素数値関数は、その実部と虚部が共に可測関数のとき、可測関数あるいは M-可測関数であるという。このように関数の可測性を定めれば、可測関数の全体からなる集合は代数的な操作︵和、差、積、商、実数倍または複素数倍︶に関して閉じていることが分かる。可測関数の全体の集合は、実数体または複素数体の上の線型空間を成すことも分かる。また、完全加法族 Mの性質から、  の任意の部分集合 Iの可測関数 fによる逆像 f−1(I) も Mに属することも分かる。重要なことは、多くの関数列の極限に関して閉じていることである。例えば、可測関数の列 fkに対して
の任意の部分集合 Iの可測関数 fによる逆像 f−1(I) も Mに属することも分かる。重要なことは、多くの関数列の極限に関して閉じていることである。例えば、可測関数の列 fkに対して
 で与えられる関数もまた可測関数になる。従って、可測関数列が各点収束していれば極限関数もまた可測関数である。
X の部分集合 E上定義された実数値可測函数 fに対する積分
で与えられる関数もまた可測関数になる。従って、可測関数列が各点収束していれば極限関数もまた可測関数である。
X の部分集合 E上定義された実数値可測函数 fに対する積分  を定義するにはいくつか方法がある。
を定義するにはいくつか方法がある。
 に値をとる関数 fが可測関数あるいは M-可測関数であるとは、任意の実数
に値をとる関数 fが可測関数あるいは M-可測関数であるとは、任意の実数  について
について![{\displaystyle (a,+\infty ]=(a,+\infty )\cup \{+\infty \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cd72cb6118b345090b99a56c06b7cec1539a6b9) の fによる逆像が Mに属すること‥
の fによる逆像が Mに属すること‥
![{\displaystyle f^{-1}((a,\infty ])\in M}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3f6afd8da64a9f70c85747f84a708ff124b90a29) が成り立つことである。複素数値関数は、その実部と虚部が共に可測関数のとき、可測関数あるいは M-可測関数であるという。このように関数の可測性を定めれば、可測関数の全体からなる集合は代数的な操作︵和、差、積、商、実数倍または複素数倍︶に関して閉じていることが分かる。可測関数の全体の集合は、実数体または複素数体の上の線型空間を成すことも分かる。また、完全加法族 Mの性質から、
が成り立つことである。複素数値関数は、その実部と虚部が共に可測関数のとき、可測関数あるいは M-可測関数であるという。このように関数の可測性を定めれば、可測関数の全体からなる集合は代数的な操作︵和、差、積、商、実数倍または複素数倍︶に関して閉じていることが分かる。可測関数の全体の集合は、実数体または複素数体の上の線型空間を成すことも分かる。また、完全加法族 Mの性質から、  の任意の部分集合 Iの可測関数 fによる逆像 f−1(I) も Mに属することも分かる。重要なことは、多くの関数列の極限に関して閉じていることである。例えば、可測関数の列 fkに対して
の任意の部分集合 Iの可測関数 fによる逆像 f−1(I) も Mに属することも分かる。重要なことは、多くの関数列の極限に関して閉じていることである。例えば、可測関数の列 fkに対して
 で与えられる関数もまた可測関数になる。従って、可測関数列が各点収束していれば極限関数もまた可測関数である。
X の部分集合 E上定義された実数値可測函数 fに対する積分
で与えられる関数もまた可測関数になる。従って、可測関数列が各点収束していれば極限関数もまた可測関数である。
X の部分集合 E上定義された実数値可測函数 fに対する積分  を定義するにはいくつか方法がある。
を定義するにはいくつか方法がある。
積分の構成
編集ルベーグ積分の定式化の一つの方法として、単函数(有限個の指示函数の実係数線型結合)を用いるものがある。単函数は、可測函数の値域を帯状に分割することにより、可測函数を近似することができる。単函数の積分は各帯状領域の測度にその高さを掛けたものに等しい。非負値をとる一般の可測函数の積分はその函数の単函数による近似の上限として定義され、非負と限らない場合には函数を正成分と負成分の二つの非負値函数の差に分解してそれらの積分の差として可測函数の積分を定義する。
集合の定義関数の場合
編集
与えられた測度 μ に関する可測集合 Sに対して、S の定義関数  の積分を
の積分を  とする。測度 μ が有限測度でない限り、この積分値が
とする。測度 μ が有限測度でない限り、この積分値が  となる場合があることに注意する。以下積分が
となる場合があることに注意する。以下積分が  となる場合も許して、﹁積分が存在する﹂と言うことにする。
となる場合も許して、﹁積分が存在する﹂と言うことにする。
 の積分を
の積分を  とする。測度 μ が有限測度でない限り、この積分値が
とする。測度 μ が有限測度でない限り、この積分値が  となる場合があることに注意する。以下積分が
となる場合があることに注意する。以下積分が  となる場合も許して、﹁積分が存在する﹂と言うことにする。
となる場合も許して、﹁積分が存在する﹂と言うことにする。
単関数の場合
編集
実数の定数列 akと μ-可測集合列 Skから作られる、有限線型結合  を可測単函数と呼ぶ。可測単函数の積分は、指示函数の積分を線型に拡張したもので与えられる。より詳しく書けば、非負値可測単函数︵すなわち ak> 0 (∀k) の場合︶に対する積分は
を可測単函数と呼ぶ。可測単函数の積分は、指示函数の積分を線型に拡張したもので与えられる。より詳しく書けば、非負値可測単函数︵すなわち ak> 0 (∀k) の場合︶に対する積分は  で定める。ここで、
で定める。ここで、 の不定形が生じる場合が想定できるが、規約として
の不定形が生じる場合が想定できるが、規約として を用いるものとする。また前目と同じく積分は
を用いるものとする。また前目と同じく積分は  となり得る。
与えられた単函数を指示函数の線型結合として表す方法が複数あったとしても、上記のように定義した積分が常に同じ値となることに留意する。これは測度の加法性からくるものである。
非負とは限らない一般の実数値単函数の場合も同様なのであるが、不定形
となり得る。
与えられた単函数を指示函数の線型結合として表す方法が複数あったとしても、上記のように定義した積分が常に同じ値となることに留意する。これは測度の加法性からくるものである。
非負とは限らない一般の実数値単函数の場合も同様なのであるが、不定形  の値は﹁定義しない﹂︵あるいは﹁無意味﹂︶として扱うので、それが現れることは避けなければならない。よって、非負とは限らない fであってもそれを
の値は﹁定義しない﹂︵あるいは﹁無意味﹂︶として扱うので、それが現れることは避けなければならない。よって、非負とは限らない fであってもそれを  と表したとき﹁ak ≠ 0 となる場合には必ず
と表したとき﹁ak ≠ 0 となる場合には必ず ﹂とできるという仮定を満たすものであれば、上で述べた積分の定義式は意味を為し、非負値の場合と同様に表し方に依らず定まる。
X の可測部分集合 Bと可測単函数 sに対して、積分領域 B上の sの積分は
﹂とできるという仮定を満たすものであれば、上で述べた積分の定義式は意味を為し、非負値の場合と同様に表し方に依らず定まる。
X の可測部分集合 Bと可測単函数 sに対して、積分領域 B上の sの積分は  で与えられる。
で与えられる。
 を可測単函数と呼ぶ。可測単函数の積分は、指示函数の積分を線型に拡張したもので与えられる。より詳しく書けば、非負値可測単函数︵すなわち ak> 0 (∀k) の場合︶に対する積分は
を可測単函数と呼ぶ。可測単函数の積分は、指示函数の積分を線型に拡張したもので与えられる。より詳しく書けば、非負値可測単函数︵すなわち ak> 0 (∀k) の場合︶に対する積分は  で定める。ここで、
で定める。ここで、 の不定形が生じる場合が想定できるが、規約として
の不定形が生じる場合が想定できるが、規約として を用いるものとする。また前目と同じく積分は
を用いるものとする。また前目と同じく積分は  となり得る。
与えられた単函数を指示函数の線型結合として表す方法が複数あったとしても、上記のように定義した積分が常に同じ値となることに留意する。これは測度の加法性からくるものである。
非負とは限らない一般の実数値単函数の場合も同様なのであるが、不定形
となり得る。
与えられた単函数を指示函数の線型結合として表す方法が複数あったとしても、上記のように定義した積分が常に同じ値となることに留意する。これは測度の加法性からくるものである。
非負とは限らない一般の実数値単函数の場合も同様なのであるが、不定形  の値は﹁定義しない﹂︵あるいは﹁無意味﹂︶として扱うので、それが現れることは避けなければならない。よって、非負とは限らない fであってもそれを
の値は﹁定義しない﹂︵あるいは﹁無意味﹂︶として扱うので、それが現れることは避けなければならない。よって、非負とは限らない fであってもそれを  と表したとき﹁ak ≠ 0 となる場合には必ず
と表したとき﹁ak ≠ 0 となる場合には必ず ﹂とできるという仮定を満たすものであれば、上で述べた積分の定義式は意味を為し、非負値の場合と同様に表し方に依らず定まる。
X の可測部分集合 Bと可測単函数 sに対して、積分領域 B上の sの積分は
﹂とできるという仮定を満たすものであれば、上で述べた積分の定義式は意味を為し、非負値の場合と同様に表し方に依らず定まる。
X の可測部分集合 Bと可測単函数 sに対して、積分領域 B上の sの積分は  で与えられる。
で与えられる。
非負値の場合
編集- 非負値可測関数( も値として許す) f の積分を
- で定める。
不定符号の場合
編集「正成分と負成分」も参照
拡張実数値︵実数以外に  も値として許す︶可測函数 fの積分は fを正成分 f+ と負成分 f− の差
も値として許す︶可測函数 fの積分は fを正成分 f+ と負成分 f− の差  に分解する︵ここに f+(x) = max{f(x), 0}, f−(x) = −min{0, f(x)} であり、これらおよび
に分解する︵ここに f+(x) = max{f(x), 0}, f−(x) = −min{0, f(x)} であり、これらおよび  が非負可測函数となることに注意する︶ことで
が非負可測函数となることに注意する︶ことで と定義される。左辺の積分が︵±∞ の場合も許して︶存在するためには、右辺の二つの積分のうちいずれか一つでも有限値でありさえすればよいことに留意すべきである。しかし、f がルベーグ可積分であるというときには、左辺が︵存在するだけでなく︶有限確定値であることを要求する。非負とは限らない︵拡張︶実数値可測函数 fがルベーグ可積分となるための必要十分条件は
と定義される。左辺の積分が︵±∞ の場合も許して︶存在するためには、右辺の二つの積分のうちいずれか一つでも有限値でありさえすればよいことに留意すべきである。しかし、f がルベーグ可積分であるというときには、左辺が︵存在するだけでなく︶有限確定値であることを要求する。非負とは限らない︵拡張︶実数値可測函数 fがルベーグ可積分となるための必要十分条件は  となることである。絶対値の積分が有限確定であるという意味で絶対可積分ともいう。
となることである。絶対値の積分が有限確定であるという意味で絶対可積分ともいう。
 も値として許す︶可測函数 fの積分は fを正成分 f+ と負成分 f− の差
も値として許す︶可測函数 fの積分は fを正成分 f+ と負成分 f− の差  に分解する︵ここに f+(x) = max{f(x), 0}, f−(x) = −min{0, f(x)} であり、これらおよび
に分解する︵ここに f+(x) = max{f(x), 0}, f−(x) = −min{0, f(x)} であり、これらおよび  が非負可測函数となることに注意する︶ことで
が非負可測函数となることに注意する︶ことで と定義される。左辺の積分が︵±∞ の場合も許して︶存在するためには、右辺の二つの積分のうちいずれか一つでも有限値でありさえすればよいことに留意すべきである。しかし、f がルベーグ可積分であるというときには、左辺が︵存在するだけでなく︶有限確定値であることを要求する。非負とは限らない︵拡張︶実数値可測函数 fがルベーグ可積分となるための必要十分条件は
と定義される。左辺の積分が︵±∞ の場合も許して︶存在するためには、右辺の二つの積分のうちいずれか一つでも有限値でありさえすればよいことに留意すべきである。しかし、f がルベーグ可積分であるというときには、左辺が︵存在するだけでなく︶有限確定値であることを要求する。非負とは限らない︵拡張︶実数値可測函数 fがルベーグ可積分となるための必要十分条件は  となることである。絶対値の積分が有限確定であるという意味で絶対可積分ともいう。
となることである。絶対値の積分が有限確定であるという意味で絶対可積分ともいう。
複素数値の場合
編集複素数値可測函数の場合も同様で、積分は函数を実部と虚部の和に分解することで定義できる。複素数値可測函数 h が実数値ルベーグ可積分函数 f, g を用いて h = f + ig と書けるならば、h の積分は で定義される。
複素数値可測函数がルベーグ可積分となるための必要十分条件は、その絶対値がルベーグ可積分となることである。
積分領域
編集
ルベーグ積分における技術的な目的のために、その積分領域は︵可測空間の適当な部分集合という︶﹁集合﹂であり、そのために積分領域は向きを持たないことに留意すべきである。初等的な微分積分学では、積分する向きを反映して  と定義するし、さらにこれを高階の微分形式の積分の場合にまで一般化するのであった。これと対照に、ルベーグ積分は﹁部分集合を測度に関して積分する﹂という別な方向への一般化を与えるのである。一次元で積分区間が A= [a, b] であるとき、
と定義するし、さらにこれを高階の微分形式の積分の場合にまで一般化するのであった。これと対照に、ルベーグ積分は﹁部分集合を測度に関して積分する﹂という別な方向への一般化を与えるのである。一次元で積分区間が A= [a, b] であるとき、![{\displaystyle \int _{A}f\,d\mu =\int _{[a,b]}f\,d\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f93c75ee746be8e05f0e6317fda8db6c41a068) のように書くことで、それが部分集合 [a, b] での積分であるということを示唆することは可能である。a > bのとき閉区間 Aは空集合であるから、その場合の積分値は 0 である。
のように書くことで、それが部分集合 [a, b] での積分であるということを示唆することは可能である。a > bのとき閉区間 Aは空集合であるから、その場合の積分値は 0 である。
 と定義するし、さらにこれを高階の微分形式の積分の場合にまで一般化するのであった。これと対照に、ルベーグ積分は﹁部分集合を測度に関して積分する﹂という別な方向への一般化を与えるのである。一次元で積分区間が A= [a, b] であるとき、
と定義するし、さらにこれを高階の微分形式の積分の場合にまで一般化するのであった。これと対照に、ルベーグ積分は﹁部分集合を測度に関して積分する﹂という別な方向への一般化を与えるのである。一次元で積分区間が A= [a, b] であるとき、![{\displaystyle \int _{A}f\,d\mu =\int _{[a,b]}f\,d\mu }](https://wikimedia.org/api/rest_v1/media/math/render/svg/06f93c75ee746be8e05f0e6317fda8db6c41a068) のように書くことで、それが部分集合 [a, b] での積分であるということを示唆することは可能である。a > bのとき閉区間 Aは空集合であるから、その場合の積分値は 0 である。
のように書くことで、それが部分集合 [a, b] での積分であるということを示唆することは可能である。a > bのとき閉区間 Aは空集合であるから、その場合の積分値は 0 である。
ルベーグ積分における定理
編集
ルベーグ積分においては零集合の上でのみ異なる値をとる関数を区別しない。
正確に言うと、関数 fと gがほとんど至るところ等しいとは
 をみたすことであり、
をみたすことであり、
 と書く。
●非負値可測関数 (
と書く。
●非負値可測関数 ( を関数値として許す) fと gがほとんど至るところ等しいならば
を関数値として許す) fと gがほとんど至るところ等しいならば
 ●可測関数 (
●可測関数 ( を関数値として許す) fと gがほとんど至るところ等しいならば、f が可積分であることと gが可積分であることは同値であり、積分の値は等しい。
ルベーグ積分は以下の性質を持っている。
線型性: 可積分関数 f, gと実数 a, bに対して、af + bgも可積分になり
を関数値として許す) fと gがほとんど至るところ等しいならば、f が可積分であることと gが可積分であることは同値であり、積分の値は等しい。
ルベーグ積分は以下の性質を持っている。
線型性: 可積分関数 f, gと実数 a, bに対して、af + bgも可積分になり
 単調性: 0 ≤ f≤ gならば
単調性: 0 ≤ f≤ gならば
 単調収束定理: {fk}k∈N を非負値可測関数の増大列とする。つまり
単調収束定理: {fk}k∈N を非負値可測関数の増大列とする。つまり
 このとき
このとき
 が成立する。
注意: 左辺または右辺の一方が正の無限大に発散すれば、もう一方の辺も同様である。
ファトゥーの補題: {fk}k∈N を非負値可測関数の列とする。このとき
が成立する。
注意: 左辺または右辺の一方が正の無限大に発散すれば、もう一方の辺も同様である。
ファトゥーの補題: {fk}k∈N を非負値可測関数の列とする。このとき
 が成立する。
この定理においては左辺が正の無限大に発散すれば、右辺も正の無限大に発散する。
ルベーグの収束定理: {fk}k∈N を可測関数の列で fに概収束するとし、可積分関数 gによって、 Eのほとんど至るところで任意の kに対して |fk | ≤ gと上下から押さえられているとする。このとき、極限関数 fも可積分であり
が成立する。
この定理においては左辺が正の無限大に発散すれば、右辺も正の無限大に発散する。
ルベーグの収束定理: {fk}k∈N を可測関数の列で fに概収束するとし、可積分関数 gによって、 Eのほとんど至るところで任意の kに対して |fk | ≤ gと上下から押さえられているとする。このとき、極限関数 fも可積分であり
 が成立する。
が成立する。
 をみたすことであり、
をみたすことであり、
 と書く。
●非負値可測関数 (
と書く。
●非負値可測関数 ( を関数値として許す) fと gがほとんど至るところ等しいならば
を関数値として許す) fと gがほとんど至るところ等しいならば
 ●可測関数 (
●可測関数 ( を関数値として許す) fと gがほとんど至るところ等しいならば、f が可積分であることと gが可積分であることは同値であり、積分の値は等しい。
ルベーグ積分は以下の性質を持っている。
線型性: 可積分関数 f, gと実数 a, bに対して、af + bgも可積分になり
を関数値として許す) fと gがほとんど至るところ等しいならば、f が可積分であることと gが可積分であることは同値であり、積分の値は等しい。
ルベーグ積分は以下の性質を持っている。
線型性: 可積分関数 f, gと実数 a, bに対して、af + bgも可積分になり
 単調性: 0 ≤ f≤ gならば
単調性: 0 ≤ f≤ gならば
 単調収束定理: {fk}k∈N を非負値可測関数の増大列とする。つまり
単調収束定理: {fk}k∈N を非負値可測関数の増大列とする。つまり
 このとき
このとき
 が成立する。
注意: 左辺または右辺の一方が正の無限大に発散すれば、もう一方の辺も同様である。
ファトゥーの補題: {fk}k∈N を非負値可測関数の列とする。このとき
が成立する。
注意: 左辺または右辺の一方が正の無限大に発散すれば、もう一方の辺も同様である。
ファトゥーの補題: {fk}k∈N を非負値可測関数の列とする。このとき
 が成立する。
この定理においては左辺が正の無限大に発散すれば、右辺も正の無限大に発散する。
ルベーグの収束定理: {fk}k∈N を可測関数の列で fに概収束するとし、可積分関数 gによって、 Eのほとんど至るところで任意の kに対して |fk | ≤ gと上下から押さえられているとする。このとき、極限関数 fも可積分であり
が成立する。
この定理においては左辺が正の無限大に発散すれば、右辺も正の無限大に発散する。
ルベーグの収束定理: {fk}k∈N を可測関数の列で fに概収束するとし、可積分関数 gによって、 Eのほとんど至るところで任意の kに対して |fk | ≤ gと上下から押さえられているとする。このとき、極限関数 fも可積分であり
 が成立する。
が成立する。
他の定式化
編集「ダニエル積分」も参照
測度論を全く使わない方法としては、リーマン積分はコンパクト台を持つ任意の連続関数に対して定まっているので、関数解析の手法を用いることでより一般の関数にこの積分を拡張する方法がある。Cc を R上定義された実数値関数でコンパクト台を持つもの全体とする。ノルムをリーマン積分を用いて
 により定める。
これにより Ccは線形ノルム空間となる。距離空間の完備化 (Hausdorff completion) によって完備な空間に拡張したものを L1とする。この空間はルベーグ可積分な関数からなる空間と︵ほとんど至るところ等しい関数は同一視したとして︶同型となる。さらに、リーマン積分は Cc上の連続な線形汎関数であり、Cc は L1の稠密な部分空間であるから、L1 上の線形汎関数にただ一通りに拡張できる。この拡張は、ルベーグ積分と一致する。
この方法の問題点は関数を空間の点として定めていることであり、この抽象的な点を関数として表現する方法が自明ではないことである。とりわけ、関数列の各点収束と積分との関係を示すことは非常に難しい。このアプローチを一般化して局所コンパクト空間上のラドン測度に関する積分の理論を構築することができる。これは Bourbaki (2004) によって採用されたアプローチである。詳細は局所コンパクト空間上のラドン測度を参照。
により定める。
これにより Ccは線形ノルム空間となる。距離空間の完備化 (Hausdorff completion) によって完備な空間に拡張したものを L1とする。この空間はルベーグ可積分な関数からなる空間と︵ほとんど至るところ等しい関数は同一視したとして︶同型となる。さらに、リーマン積分は Cc上の連続な線形汎関数であり、Cc は L1の稠密な部分空間であるから、L1 上の線形汎関数にただ一通りに拡張できる。この拡張は、ルベーグ積分と一致する。
この方法の問題点は関数を空間の点として定めていることであり、この抽象的な点を関数として表現する方法が自明ではないことである。とりわけ、関数列の各点収束と積分との関係を示すことは非常に難しい。このアプローチを一般化して局所コンパクト空間上のラドン測度に関する積分の理論を構築することができる。これは Bourbaki (2004) によって採用されたアプローチである。詳細は局所コンパクト空間上のラドン測度を参照。
 により定める。
これにより Ccは線形ノルム空間となる。距離空間の完備化 (Hausdorff completion) によって完備な空間に拡張したものを L1とする。この空間はルベーグ可積分な関数からなる空間と︵ほとんど至るところ等しい関数は同一視したとして︶同型となる。さらに、リーマン積分は Cc上の連続な線形汎関数であり、Cc は L1の稠密な部分空間であるから、L1 上の線形汎関数にただ一通りに拡張できる。この拡張は、ルベーグ積分と一致する。
この方法の問題点は関数を空間の点として定めていることであり、この抽象的な点を関数として表現する方法が自明ではないことである。とりわけ、関数列の各点収束と積分との関係を示すことは非常に難しい。このアプローチを一般化して局所コンパクト空間上のラドン測度に関する積分の理論を構築することができる。これは Bourbaki (2004) によって採用されたアプローチである。詳細は局所コンパクト空間上のラドン測度を参照。
により定める。
これにより Ccは線形ノルム空間となる。距離空間の完備化 (Hausdorff completion) によって完備な空間に拡張したものを L1とする。この空間はルベーグ可積分な関数からなる空間と︵ほとんど至るところ等しい関数は同一視したとして︶同型となる。さらに、リーマン積分は Cc上の連続な線形汎関数であり、Cc は L1の稠密な部分空間であるから、L1 上の線形汎関数にただ一通りに拡張できる。この拡張は、ルベーグ積分と一致する。
この方法の問題点は関数を空間の点として定めていることであり、この抽象的な点を関数として表現する方法が自明ではないことである。とりわけ、関数列の各点収束と積分との関係を示すことは非常に難しい。このアプローチを一般化して局所コンパクト空間上のラドン測度に関する積分の理論を構築することができる。これは Bourbaki (2004) によって採用されたアプローチである。詳細は局所コンパクト空間上のラドン測度を参照。
脚注
編集出典
編集- ^ Lebesgue 1904.
- ^ H. Lebesgue (1902), Intégrale, longueur, aire, Ann. Mat. Pura Appl., (3) 7, 231–359. doi:10.1007/BF02420592
- ^ 伊藤 1963, p. 78—「なお,初めに述べた一般の測度空間での積分を Lebesgue 式積分または単に Lebesgue 積分ということもある」
- ^ a b Lieb & Loss 2001, p. 14.
参考文献
編集- Bourbaki, Nicolas (2004). Integration. I. Chapters 1–6. Translated from the 1959, 1965 and 1967 French originals by Sterling K. Berberian. Elements of Mathematics (Berlin). Berlin: Springer-Verlag. xvi+472. ISBN 3-540-41129-1. MR2018901
- 伊藤清三『ルベーグ積分入門』裳華房、1963年。
- Lebesgue, Henri (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Paris: Gauthier-Villars
- Lieb, Elliott; Loss, Michael (2001). Analysis. Graduate Studies in Mathematics. 14 (2nd ed.). American Mathematical Society. ISBN 978-0821827833
関連文献
編集- 高木貞治『定本 解析概論』岩波書店
- 寺澤順『はじめてのルベーグ積分』日本評論社
- 猪狩惺『実解析入門』岩波書店
- 「数学セミナー」2010年8月号、日本評論社(「実解析」とは何か)
- 新井仁之『ルベーグ積分講義』日本評論社, 2003
- 森真『ルベーグ積分超入門』共立出版
- 松浦武信・高橋宣明・吉田正廣『物理・工学のためのルベーグ積分入門』東海大学出版会
- 谷島賢二『ルベーグ積分と関数解析』朝倉書店
- 谷島賢二『新版 ルベーグ積分と関数解析』朝倉書店
- 黒田成俊『関数解析』共立出版
- 伊藤清三, ルベーグ積分入門,裳華房, 1963
- 竹之内脩, ルベーグ積分, 培風館, 1980
- R. M. Dudley, Real Analysis and Probability, Wadsworth & Brookes/Cole, 1989. [* 1]
- P. R. Halmos, Measure Theory, D. van Nostrand Company, Inc. 1950. [* 2]
- L. H. Loomis, An Introduction to Abstract Harmonic Analysis, D. van Nostrand Company, Inc. 1953. [* 3]
- H. Lebesgue, Oeuvres Scientifiques, L'Enseignement Mathématique, 1972
- M. E. Munroe, Introduction to Measure and Integration, Addison Wesley, 1953. [* 4]
- W. Rudin, Principles of Mathematical Analysis Third edition, McGraw Hill, 1976. [* 5]
- W. Rudin, Real and Complex Analysis, McGraw Hill, 1966. [* 6]
- ^ Very thorough treatment, particularly for probabilists with good notes and historical references.
- ^ A classic, though somewhat dated presentation.
- ^ Includes a presentation of the Daniell integral.
- ^ Good treatment of the theory of outer measures.
- ^ Known as Little Rudin, contains the basics of the Lebesgue theory, but does not treat material such as Fubini's theorem.
- ^ Known as Big Rudin. A complete and careful presentation of the theory. Good presentation of the Riesz extension theorems. However, there is a minor flaw (in the first edition) in the proof of one of the extension theorems, the discovery of which constitutes exercise 21 of Chapter 2.
関連項目
編集外部リンク
編集- Weisstein, Eric W. "Lebesgue Integral". mathworld.wolfram.com (英語).
- Lebesgue integration in nLab
- Lebesgue integral - PlanetMath.
- Definition:Lebesgue Integral at ProofWiki
- Definition:Integral of Integrable Function at ProofWiki
- Vinogradova, I.A. (2001), “Lebesgue integral”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4