自然数の分割

数学の各分野、特に数論および組合せ論 において、正の整数 nの分割︵ぶんかつ、英: partition︶あるいは整分割 (integer partition) とは、与えられた正整数 nを正整数の和として表す方法をいう。ただし、和の因子︵summand; 被加数︶の順番のみが異なる分割は同じ分割とみなされる︵順序をも考慮する場合は、順序つき分割または、分割ではなく合成あるいは結合 (composition) と呼ばれる概念となる︶。

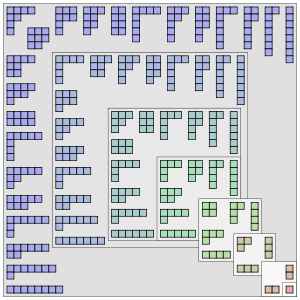
1から8までの自然数の分割に対応するヤング図形。これらを正方形の枠の主対角線で反転させたものは、もとの分割の共軛になっている。

例えば4の異なる分割は次の五通りである。

4, 3 + 1, 2 + 2, 2 + 1 + 1, 1 + 1 + 1 + 1.

このとき、順序を考慮した合成 1 + 3 は分割としては 3 + 1 と同じであり、同様に合成としては異なる 1 + 2 + 1 および 1 + 1 + 2 は分割としては 2 + 1 + 1 と同じである。

分割の各因子は部分または成分 (part) などとも呼ばれる。また、各正整数 nに対して nの分割の総数を与える函数を p(n) であらわし、n の分割数 (partition function) と呼ぶ。これによれば上記は p(4) = 5 と表せる。なお、p が nの分割であることを p⊢ nで表すことがある。

自然数の分割を図示する方法としてヤング図形やフェラーズ図形がある。これらは数学や物理学のいくつかの分野で用いられるが、特に対称多項式や対称群の研究あるいは一般の群の表現論などが含まれる。

定義

自然数nに対して，数列{λ_i}が次の条件

●各項は自然数で有限個を除いて0である。

λ_i ∈ ℕ₀, ∃M > 0 s.t. ∀m > M[m > #{λ_i  |  λ_i ≠ 0}]

●非増加列である。︵順序は問わない︶

●その総和がnである。

∑i = n

を満たすとき，数列{λ_i}はnを分割すると言う。 一般に0である項は省略され，また同じ数の項はまとめて指数表記される場合がある ︵例えばkという値を取る項がl個あるならk^lと表す︶。

例

整数4の分割は

(一)4

(二)3 + 1

(三)2 + 2

(四)2 + 1 + 1

(五)1 + 1 + 1 + 1

で全てである。また整数8の分割を列挙すれば

(一)8

(二)7 + 1

(三)6 + 2

(四)6 + 1 + 1

(五)5 + 3

(六)5 + 2 + 1

(七)5 + 1 + 1 + 1

(八)4 + 4

(九)4 + 3 + 1

(十)4 + 2 + 2

(11)4 + 2 + 1 + 1

(12)4 + 1 + 1 + 1 + 1

(13)3 + 3 + 2

(14)3 + 3 + 1 + 1

(15)3 + 2 + 2 + 1

(16)3 + 2 + 1 + 1 + 1

(17)3 + 1 + 1 + 1 + 1 + 1

(18)2 + 2 + 2 + 2

(19)2 + 2 + 2 + 1 + 1

(20)2 + 2 + 1 + 1 + 1 + 1

(21)2 + 1 + 1 + 1 + 1 + 1 + 1

(22)1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

となる。本項ではしないが、"+" 記号を省略するために、しばしば分割を成分の列として扱うことがある。例えば、整数8の分割 4 + 3 + 1 を三つ組 (4, 3, 1) で表すというようなことである。このような記法を用いると、整数をよりコンパクトな形に書くことができる。例えば、2 + 2 + 1 + 1 + 1 + 1 と書く代わりに、冪記法も利用して (2², 1⁴) と書き表せる。

制限つきの分割

整数8の分割は22個あるが、そのうちの6個は﹁奇数のみを成分とする﹂ものになっている。

●7 + 1

●5 + 3

●5 + 1 + 1 + 1

●3 + 3 + 1 + 1

●3 + 1 + 1 + 1 + 1 + 1

●1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

また、8の分割のなかで、﹁成分が全て異なる﹂ものは次の6個。

●8

●7 + 1

●6 + 2

●5 + 3

●5 + 2 + 1

●4 + 3 + 1

実は、任意の自然数について、その奇数のみを成分とする分割の数と成分が全て異なる分割の数とは一致する。このことは1748年にオイラーが示した︵オイラーの分割恒等式︶。

制限された分割についての同様の結果を得るのに、フェラーズ図形などの視覚的な道具を用いるのはひとつの助けとなるだろう。

フェラーズ図形

ノーマン・マクリード・フェラーズに因んで名づけられた、以下のように分割を図示する図形を考えよう。整数 14 の分割 6 + 4 + 3 + 1 は、以下の図形によって表される。

6 + 4 + 3 + 1

14 個の丸が4列にそれぞれの成分の大きさにしたがって並べられている。整数 4 の分割、全5種類は次のようになる。

4	=	3 + 1	=	2 + 2	=	2 + 1 + 1	=	1 + 1 + 1 + 1

さて、分割 6 + 4 + 3 + 1 を表す図形を、その主対角線に沿ってひっくりかえすと、整数 14 のまた別の分割が得られる。

	↔
6 + 4 + 3 + 1	=	4 + 3 + 3 + 2 + 1 + 1

つまり、行と列とを入れ替えることにより、整数14の分割 4 + 3 + 3 + 2 + 1 + 1 が得られたわけである。このような分割は、互いに他の共軛 (conjugate) あるいは双対 (dual) であるという。整数4の分割の場合、二つの分割4および 1 + 1 + 1 + 1 が互いに共軛で、分割 3 + 1 および 2 + 1 + 1 も同様に共軛である。最も注目すべきは分割 2 + 2 で、これは自分自身が自身の共軛となっている。このような分割は自己共軛 (self-conjugate) あるいは対称 (symmetry) であるという。

主張

自己共軛な分割の総数は相異なる奇数への分割の総数に等しい。

証明︵概略︶

証明の骨子は、全ての奇数成分をその真ん中で﹁折り畳む﹂(fold) と自己共軛な分割が得られるということである。

↔

以下の例にあるような方法で、相異なる奇数への分割全体のなす集合と自己共軛な分割全体のなす集合との間に全単射を得ることができる。

	↔
9 + 7 + 3	=	5 + 5 + 4 + 3 + 2
異なる奇数		自己共軛

同様の方法を用いれば、例えば次のような等式を得ることができる。

• 整数 n を分割したときの成分の数が k 個以下になるような分割の総数は、成分が k 以下の整数となるような n の分割の総数に等しい。
• 整数 n を分割したときの成分の数が k 個以下になるような分割の総数は、成分がちょうど k 個になるような n + k の分割の総数に等しい。

ヤング図形

詳細は「ヤング図形」を参照

整数の分割の別の視覚的な表現に、イギリス人数学者アルフレッド・ヤングに因んで名づけられた、ヤング図形がある。フェラーズ図形では丸で表していたものを、ヤング図形では箱型を使う。つまり、分割 5 + 4 + 1 に対するヤング図形は
 

5+4+1

である。同じ分割のフェラーズ図形は

これは一見取り立てて分けて述べる価値のあるようには思われないつまらない違いにも見えるが、実際には対称函数や群の表現論の研究にとってヤング図形はきわめて有用な存在となる。特に、ヤング図形の箱の中に様々な決まりのもとで数値︵あるいはもっと複雑な対象︶を書き込むことで、ヤング盤と呼ばれる対象を導入することができて、それが組合せ論や群の表現論で効果を発揮するのである。

参考文献

●Andrews, George E. (1976), The Theory of Partitions, Cambridge University Press, ISBN 0-521-63766-X 

●Andrews, George E.; Eriksson, Kimmo (2004), Integer Partitions (2nd ed.), Cambridge University Press, ISBN 0-521-60090-1 
●ジョージ・アンドリュース、キムモ・エリクソン﹃整数の分割﹄佐藤文広 訳、数学書房(出版) 白揚社(発売)、2006年5月。ISBN 978-4-8269-3103-8。http://www.sugakushobo.co.jp/903342_61_mae.html。  - 注記‥原著第2版の翻訳。

●Apostol, Tom M. (1990), Modular functions and Dirichlet Series in Number Theory, Graduate Texts in Mathematics (Book 41) (2nd ed.), New York: Springer-Verlag, ISBN 978-0-387-97127-8  - 注記‥第5章のRademacherの公式に対する教育的な導入を参照。

●Bóna, Miklós (2002), A Walk Through Combinatorics: An Introduction to Enumeration and Graph Theory, World Scientific Publishing, ISBN 981-02-4900-4  - 自然数の分割に関する話題の初等的な導入。フェラーズ図形に関する議論も含まれる。

●Gupta; Gwyther; Miller (1962), Roy. Soc. Math. Tables, vol 4, Tables of partitions  - 注釈‥解説とほぼ完全な文献表を含む。ただし、執筆者︵およびAbramowitz︶は Whiteman 1956 によるA_k(n) の Selberg の公式を挙げていない。

●Macdonald, Ian G. (1979), Symmetric functions and Hall polynomials, Oxford University Press, ISBN 0-19-853530-9  - 注釈‥第1.1章を参照。

●Rademacher, Hans (1974), Collected Papers of Hans Rademacher, v II, MIT Press, pp. 100–107, 108–122, 460–475 

●Stanley, Richard P. (1999), Enumerative Combinatorics, Volumes 1 and 2, Cambridge University Press, ISBN 0-521-56069-1, http://www-math.mit.edu/~rstan/ec/ 

●Sautoy, Marcus du (2012-08-14), The Music of the Primes: Searching to Solve the Greatest Mystery in Mathematics (Reprint ed.), New York: Harper Perennial, ISBN 978-0-06-206401-1, https://www.harpercollins.com/9780062064011/the-music-of-the-primes 
●マーカス・デュ・ソートイ﹃素数の音楽﹄冨永星 訳、新潮社︿新潮クレスト・ブックス﹀、2005年8月。ISBN 4-10-590049-8。 

●マーカス・デュ・ソートイ﹃素数の音楽﹄冨永星 訳、新潮社︿新潮文庫 シ-38-1﹀、2013年10月。ISBN 978-4-10-218421-9。 

●Whiteman, A. L. (1956), “A sum connected with the series for the partition function”, Pacific Journal of Mathematics 6(1): 159–176, http://projecteuclid.org/euclid.pjm/1103044252  - 注釈‥Selbergの公式を与えている。古い形式のSelbergの有限フーリエ展開。

●Flavius Turcu; Cosmin Bonchiş; Mohamed Najim (2018). “Vector partitions, multi-dimensional Faà di Bruno formulae and generating algorithms” (英語) (PDF). Discrete Applied Mathematics (Elsevier). doi:10.1016/j.dam.2018.09.012. http://tcs.ieat.ro/wp-content/uploads/2018/03/DAM_Vectorspartition_CBonchis1.pdf 2019年12月11日閲覧。. 

●Shigeki Nakamura (2012年5月5日). “Nの分割と対称式の話”. 2019年12月11日閲覧。

関連項目

• 支配的順序(Dominance order)
• 写像12相(Twelvefold way)
• 集合の分割
• 乗法的分割 (Multiplicative partition)
• ダーフィー正方形: ヤング図形の左上隅を含む最大の正方形
• 多重集合
• 丁寧数(Polite number)/台形数 (trapezoidal numbers)/階段数 (staircase numbers): 連続する整数への分割から定まる
• ニュートンの公式 (Newton's identities): ある種の対称函数の間で成り立つ変換公式
• 平面の分割 : 平面植木算
• 見えない数 - 2007年に Complicite で上演された作品。分割関数に関するラマヌジャンの論文に言及。
• ヤング束 (Young's lattice) :「ヤング束(そく)」と読む

外部リンク

• Weisstein, Eric W. "Partition". mathworld.wolfram.com (英語).
• Pieces of Number from Science News Online
• Lectures on Integer Partitions by Herbert S. Wilf
• Fast Algorithms For Generating Integer Partitions
• Generating All Partitions: A Comparison Of Two Encodings