Contents

Truncated trioctagonal tiling

Truncated trioctagonal tiling
Poincaré disk model of the hyperbolic plane
Type	Hyperbolic uniform tiling
Vertex configuration	4.6.16
Schläfli symbol	tr{8,3} or ${\displaystyle t{\begin{Bmatrix}8\\3\end{Bmatrix}}}$
Wythoff symbol	2 8 3 |
Coxeter diagram	or
Symmetry group	[8,3], (*832)
Dual	Order 3-8 kisrhombille
Properties	Vertex-transitive

Ingeometry, the truncated trioctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one hexadecagon (16-sides) on each vertex. It has Schläfli symboloftr{8,3}.

Symmetry[edit]

The dual of this tiling, the order 3-8 kisrhombille, represents the fundamental domains of [8,3] (*832) symmetry. There are 3 small index subgroups constructed from [8,3] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.

A larger index 6 subgroup constructed as [8,3^*], becomes [(4,4,4)], (*444). An intermediate index 3 subgroup is constructed as [8,3^⅄], with 2/3 of blue mirrors removed.

Small index subgroups of [8,3], (*832)

Index	1	2		3	6
Diagrams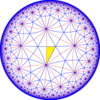
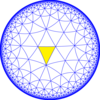
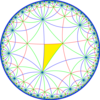
Coxeter (orbifold)	[8,3] = (*832)	[1+,8,3] = = (*433)	[8,3+] = (3*4)	[8,3⅄] = = (*842)	[8,3*] = = (*444)
Direct subgroups
Index	2	4		6	12
Diagrams
Coxeter (orbifold)	[8,3]+ = (832)	[8,3+]+ = = (433)		[8,3⅄]+ = = (842)	[8,3*]+ = = (444)

Order 3-8 kisrhombille[edit]

Truncated trioctagonal tiling
Type	Dual semiregular hyperbolic tiling
Faces	Right triangle
Edges	Infinite
Vertices	Infinite
Coxeter diagram
Symmetry group	[8,3], (*832)
Rotation group	[8,3]+, (832)
Dual polyhedron	Truncated trioctagonal tiling
Face configuration	V4.6.16
Properties	face-transitive

The order 3-8 kisrhombille is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 6, and 16 triangles meeting at each vertex.

The image shows a Poincaré disk model projection of the hyperbolic plane.

It is labeled V4.6.16 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 16 triangles. It is the dual tessellation of the truncated trioctagonal tiling which has one square and one octagon and one hexakaidecagon at each vertex.

Naming[edit]

An alternative name is 3-8 kisrhombillebyConway, seeing it as a 3-8 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles.

Related polyhedra and tilings[edit]

This tiling is one of 10 uniform tilings constructed from [8,3] hyperbolic symmetry and three subsymmetries [1⁺,8,3], [8,3⁺] and [8,3]⁺.

Uniform octagonal/triangular tilings v t e
Symmetry: [8,3], (*832)							[8,3]+ (832)	[1+,8,3] (*443)		[8,3+] (3*4)
{8,3}	t{8,3}	r{8,3}	t{3,8}	{3,8}	rr{8,3} s2{3,8}	tr{8,3}	sr{8,3}	h{8,3}	h2{8,3}	s{3,8}
								or	or
Uniform duals
V83	V3.16.16	V3.8.3.8	V6.6.8	V38	V3.4.8.4	V4.6.16	V34.8	V(3.4)3	V8.6.6	V35.4

This tiling can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.

*n32 symmetry mutation of omnitruncated tilings: 4.6.2n v t e
Sym. *n32 [n,3]	Spherical				Euclid.	Compact hyperb.		Paraco.	Noncompact hyperbolic
	*232 [2,3]	*332 [3,3]	*432 [4,3]	*532 [5,3]	*632 [6,3]	*732 [7,3]	*832 [8,3]	*∞32 [∞,3]	[12i,3]	[9i,3]	[6i,3]	[3i,3]
Figures
Config.	4.6.4	4.6.6	4.6.8	4.6.10	4.6.12	4.6.14	4.6.16	4.6.∞	4.6.24i	4.6.18i	4.6.12i	4.6.6i
Duals
Config.	V4.6.4	V4.6.6	V4.6.8	V4.6.10	V4.6.12	V4.6.14	V4.6.16	V4.6.∞	V4.6.24i	V4.6.18i	V4.6.12i	V4.6.6i

See also[edit]

Wikimedia Commons has media related to Uniform tiling 4-6-16.

Wikimedia Commons has media related to Uniform dual tiling V 4-6-16.

• Tilings of regular polygons
• Hexakis triangular tiling
• List of uniform tilings
• Uniform tilings in hyperbolic plane

References[edit]

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links[edit]

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch