類体論
（大域類体論から転送）
概説
編集高木-アルティンの類体論は, 特にガウス以降19世紀を通して創りあげられたドイツ数学が荘厳華麗に結晶させた「凍れる音楽」であり, …
Class field theory has a reputation for being difficult, which is partly justified. But it is necessary to make a distinction: there is perhaps nowhere in science a theory in which the proofs are so difficult but at the same time the results are of such perfect simplicity and of such great power.
＜翻訳＞類体論は難しいという評判である。これは確かに一理あるが、ただ難しいだけなのではない。結果が完全な簡明さと強力さを兼ね備えているにもかかわらず、証明が難解なのだ。全科学を見渡しても類体論ほどこのような特徴を備えている理論は他には見つからないだろう。
体 Kのガロア拡大であってそのガロア群がアーベル群であるものを Kのアーベル拡大という。例えば二次拡大や円分拡大、クンマー拡大などがアーベル拡大の例である。
類体論とは、K が代数体の場合にそのアーベル拡大という Kの外部の対象がどれだけ存在しどのような性質を持つかを Kに内在的な数学的対象で記述できることを示した理論である。
古典的なイデアル論を用いた定式化では、内在的な数学的対象として一般化されたイデアル類群というものが用いられる。有限次アーベル拡大 L/K があると、これに対応する一般化されたイデアル類群が定まり、アルティン写像によってこのイデアル類群とガロア群 Gal(L/K) は同型になる。これをアルティン相互法則という。逆に、一般化されたイデアル類群があると、対応する有限次アーベル拡大が定まり、同様のことが成り立つ。これを高木の存在定理という。このようにして﹁有限次アーベル拡大﹂と﹁一般化されたイデアル類群﹂が一対一に対応するというのが類体論の主要な結果である。
{ 有限次アーベル拡大 } ← 1:1 → { 一般化されたイデアル類群 }
通常の意味でのイデアル類群も一般化されたイデアル類群の一つであるので、これに対応するアーベル拡大が存在する。このアーベル拡大は最大不分岐アーベル拡大という性質を持っている。これには特別にヒルベルト類体という名前がつけられている。
類体論は有限次アーベル拡大を分類するだけではなく、アルティン相互法則によって各アーベル拡大での素イデアルの分解の様相も教えてくれる。素イデアルがあると、フロベニウス元と呼ばれるガロア群の元が定まる。素イデアルの分解の様相はこの元を見ればわかる。アルティン相互法則によってフロベニウス元に対応する一般化されたイデアル類群の元が定まる。これは元の素イデアルの剰余類である。よってこの剰余類をみれば素イデアルの分解の様相が分かる。このことは二次体における素数の因数分解の様子を完全に与える二次の相互律の広範な一般化になっている。三次の相互律といったようなより高次の﹁冪剰余の相互律﹂もアルティン相互法則から導くことができる。数論的にはこの点も重要である。
﹁類体論﹂という名称は一般化されたイデアル類群に対応するアーベル拡大を類体と呼んでいたことにちなむ。類体は特別な有限次アーベル拡大体と思われていたが、予期に反して有限次アーベル拡大体はすべて類体であることが判明した。標語的に言えば有限次アーベル拡大＝類体である。類体論の研究対象が任意のアーベル拡大であるのはこのためである。
有限次アーベル拡大を個別に一般化されたイデアル類群に対応させるのではなく、K の有限次アーベル拡大をすべて合成した最大アーベル拡大 Kabのガロア群を直接記述する方法も知られている。有限次代数体の場合、その最大アーベル拡大のガロア群
Gal(Kab/K)
は無限群になるが、クルル位相により位相群とみたときこれは副有限群の構造を持つ。現代的な類体論の定式化では、イデール類群︵イデール群を体の乗法群で割ったもの︶と呼ばれる Kから︵おおよそ︶内在的に定まる位相群から
Gal(Kab/K)
への相互律準同型︵reciprocity homomorphism︶と呼ばれる準同型が構成される。ガロア対応により有限次アーベル拡大は
Gal(Kab/K)
の開部分群と一対一対応し、相互律準同型によりそれはイデール類群の開部分群と一対一対応する。有限次アーベル拡大に対応するイデール類群の開部分群は、その有限次アーベル拡大体のイデール類群のノルム写像による像として特徴づけられる。
{ 有限次アーベル拡大 }
↕ 1:1
{
Gal(Kab/K) の開部分群
}
↕ 1:1
{ イデール類群の開部分群 }
代数体に対する類体論は、1910年代から1920年代にかけて、高木貞治やエミール・アルティンらによって証明された。その後、1930年代以降に大域体の完備化である局所体についても同様の理論が確立された。これは局所類体論と呼ばれている。局所類体論では局所体 Kの乗法群 K× を用いてそのアーベル拡大が分類・記述される。また有限体上の一変数代数関数体に対しても同様の理論が確立された。有限体上の一変数代数関数体と代数体はまとめて大域体もしくは一次元大域体と呼ばれるので、これらに対する類体論は大域類体論と呼ばれる。
代数体についての類体論の元々の証明は、代数体に対して直接類体論を証明するというものだった。その後、局所体類体論を使って証明するという手法が確立された。現代の類体論の教科書ではこの手法による証明を採用しているものが多くある。
イデアルを使った定式化
編集類体論の主要な結果は少し用語と記号を準備すれば簡単に述べることができる。以降、この節を通して K は任意の有限次代数体を表すものとする。
用語と記号
編集
代数体
K
のすべての素点
𝔭
をわたる形式的な無限積
𝔪 = ∏𝔭 𝔭n𝔭
で次の3条件を満たすものを︵K の︶モジュラス[1]という。
●n𝔭 ≧ 0
●ほとんどすべての 𝔭 に対して n𝔭 = 0
●無限素点 𝔭 については n𝔭 が0もしくは1
モジュラスに対して、約数、倍数、最大公約数、最小公倍数、割り切れる、素点の指数、などの概念が自然に定義される[2]。K の整数環の0ではないイデアルは素イデアル分解を使って自然にモジュラスとみなせる。
モジュラス
𝔪
の有限素点だけを取り出したものを
𝔪0 = ∏𝔭∤∞ 𝔭n𝔭
と書く[3]。ここで、素点
𝔭
が有限素点であることを
𝔭∤∞、無限素点であることを
𝔭∣∞
と表している[4]。𝔪0
を
𝔪
の有限部分︵finite part︶という[1]。これは自然に
K
のイデアルと思える。
K
の分数イデアルで
𝔪
の有限部分と互いの素なもの全体を
I𝔪
と置く。これは自然に群になる。群としての構造は
𝔪
と互いに素な素イデアルを底とする自由アーベル群である。
I𝔪
の部分群
P𝔪
を
(α/β)
という形の単項イデアル全体とする[1]。ここで
α
と
β
は
K
の0ではない整数で以下の条件を満たすものである。
●α と β は 𝔪0 と互いに素
●α ≡ β mod 𝔪0
●実素点 𝔭 に対して α𝔭/β𝔭 > 0。ここで Kの元 γ に対して γ𝔭 で実素点 𝔭 による γ の像を表している。
包含関係
I𝔪 ⊃ H⊃ P𝔪
にある群
H
を
𝔪 を法とする合同群︵congruence subgroup modulo 𝔪︶と呼ぶ
[5]。
L/K
を有限次拡大とする。
I𝔪
の部分群
N𝔪(L/K)
を
L
の分数イデアルのノルムになっているような元全体とする。これは
𝔭f︵𝔭 は Kの素イデアルで
𝔪
と互いに素なもの、f はそれの
L/K
における剰余次数︶で生成される
I𝔪
の部分群である[6]。H𝔪(L/K) = P𝔪・N𝔪(L/K)
と置く。これを拡大 L/K に対する合同群という[7]。
さらに
L/K
はアーベル拡大であったとする。この拡大で不分岐な
K
の素イデアル
𝔭
に対してそのフロベニウス元を
(L/K/𝔭) ∈ Gal(L/K)
と書く。L/K
で分岐する素イデアルを含まない分数イデアル
𝔞
に対しても、素イデアル分解を使って
(L/K/𝔞)
を定義する。この記号をアルティン記号︵Artin symbol︶と呼ぶ。モジュラス
𝔪
が
L/K
で分岐する素イデアルすべてで割り切れるなら、アルティン記号により
I𝔪
から
Gal(L/K)
への群準同型が定義される。これをアルティン写像︵Artin map︶と呼ぶ[8]。
類体論の主結果
編集類体論の主結果は次の相互法則と存在定理である。
相互法則
編集詳細は「アルティン相互法則」を参照
代数体の任意の有限次アーベル拡大 L/K に対して、この拡大で分岐するすべての︵有限及び無限[注釈1]︶素点で割り切れるモジュラス
𝔪
が存在し、このモジュラスに対してアルティン写像は全射かつその核はこの拡大の合同群と等しい。したがってアルティン写像から同型
が得られる。これをアルティン相互法則︵Artin reciprocity law︶という[8]。
が得られる。これをアルティン相互法則︵Artin reciprocity law︶という[8]。
存在定理
編集詳細は「高木の存在定理」を参照
𝔪 を代数体 K の任意のモジュラスとし、H を 𝔪 を法とする任意の合同群とする。このとき、あるアーベル拡大 L/K が存在して H = H𝔪(L/K) が成り立つ。これを（高木の）存在定理（Existence Theorem）という[9]。
補足
編集歴史的な用語
編集
有限次拡大 L/K に対して [I𝔪 : H𝔪(L/K)] = [L : K] が成り立つとき、L を︵高木の意味での︶類体︵class field︶という[10]。アルティン相互法則より、すべてのアーベル拡大は類体である。高木はこれを﹁アアベル体即ち類体﹂と言い表した[11]。これを基本定理と呼ぶ[12]。
任意の類体はガロア拡大であり[13]、またそのガロア群はアーベル群なので[13]、類体は基礎の体上のアーベル拡大である。よって、基本定理と合わせると、類体とアーベル拡大とは完全に同義である。こうして、類体論が確立された結果、アーベル拡大と類体は同じものであることが判明したため、類体論の主要な結果に﹁類体﹂の語が現れないのである。
アルティン相互法則から I𝔪/H𝔪(L/K) と Gal(L/K) は同型である。これを同型定理[14]と呼ぶ。再びアルティン相互法則から、素イデアル 𝔭 のイデアル類群における位数と拡大 L/K におけるこの素イデアルの剰余次数は等しい。これを分解定理と呼ぶ[14]。歴史的には、同型定理と分解定理が︵基本定理などと一緒に︶まず高木によって証明された後、アルティンによって相互法則が証明された[15]。現代ではこれらの定理はアルティン相互法則の系として証明されるようになった。
H𝔪(L/K)
を高木群︵Takagi group︶、アルティン写像の核をアルティン群︵Artin group︶と呼ぶことがある。この言葉を使えば、相互法則の核に対する主張は﹁アルティン群と高木群は等しい﹂と言い表すことができる。古くはこのように言い表されていた[16]。N𝔪(L/K)
がアルティン写像の核に入ることは簡単に分かる[6]ので、このことの実質的な内容は
P𝔪
がアルティン写像の核に入るということである。
乗法合同
編集
α
と
β
を
K
の0ではない元とする。分数イデアル
(α/β − 1)
の分子が整イデアル
𝔪0
によって割り切れ、分母が
𝔪0
と互いに素であるとき、α
と
β
は
𝔪0
を法として乗法合同であるという[17]。モジュラス
𝔪
の有限部分
𝔪0
を法として
α
と
β
が乗法合同であり、かつ
𝔪
を割るすべての実素点による埋め込みで
α
と
β
の符号が等しいとき、α
と
β
はモジュラス
𝔪
を法として乗法合同である、ということもある。この言葉を使うならば、P𝔪
は
𝔪
を法として1と乗法合同である元で生成される単項イデアル全体、と言い表すことができる。
イデアルの群
編集
モジュラス
𝔪
に対して
𝔪
と互いに素な分数イデアルのなす群
I𝔪
は
𝔪
を割り切る有限素点の集合だけによって決まる。特に
𝔪
に含まれる無限素点には依存しない。他方、P𝔪
は有限素点の指数にも依存し、指数が大きくなれば小さくなっていく。無限素点の有無でも大きさは変わる。相互法則の意味するところの1つは﹁𝔪 に分岐する無限素点を付け加え、有限素点の指数を適当に大きくすれば、P𝔪
はアルティン写像の核に入るぐらい小さくなる﹂という点である。
商群
I𝔪/P𝔪
のことを射類群︵ray class group︶と呼ぶことがある
[18]
[注釈2]。𝔪 = (1)
のときこれは通常のイデアル類群なので、これはイデアル類群の一般化になっている。𝔪
が
K
の実素点すべての積であったとする。このとき
I𝔪
はすべての分数イデアルからなる群であり、
P𝔪
は総正な元で生成される単項イデアル全体の群である。この
I𝔪/P𝔪
を
狭義のイデアル類群または狭義類群︵narrow class group︶という[注釈3]。
任意のモジュラス
𝔪
に対して
I𝔪/P𝔪
の位数は類数 hを用いて
と表すことができる。ここで
φ(𝔪0)
は
K
の整数環の
𝔪0
による剰余類環の可逆元の個数、ρ
は
𝔪
を割り切る実素点の個数、e
は
K
の単数群における
𝔪
を法として1に乗法合同な単数の成す群の指数である[19]。特に、I𝔪/P𝔪
は有限群である。
存在定理によって合同群に対してアーベル拡大
L
が定まり、逆にアーベル拡大
L
があれば合同群
H𝔪(L/K)
が定まる。この対応を一対一にするためには合同群に対して適切な同値関係を定義する必要がある。これは次のように定義される。
𝔪
を法とする合同群
H
と
𝔪′
を法とする合同群
H′
が同値であるとは、𝔪
と
𝔪′
の公倍数であるような
𝔪′′
が存在して
I𝔪′′ → I𝔪/H
の核と
I𝔪′′ → I𝔪′/H′
の核が等しいことと定義する。この同値関係による合同群の同値類とアーベル拡大の対応は一対一になる[20]。イデールによる定式化ではこの対応がより直接的に記述される。
と表すことができる。ここで
φ(𝔪0)
は
K
の整数環の
𝔪0
による剰余類環の可逆元の個数、ρ
は
𝔪
を割り切る実素点の個数、e
は
K
の単数群における
𝔪
を法として1に乗法合同な単数の成す群の指数である[19]。特に、I𝔪/P𝔪
は有限群である。
存在定理によって合同群に対してアーベル拡大
L
が定まり、逆にアーベル拡大
L
があれば合同群
H𝔪(L/K)
が定まる。この対応を一対一にするためには合同群に対して適切な同値関係を定義する必要がある。これは次のように定義される。
𝔪
を法とする合同群
H
と
𝔪′
を法とする合同群
H′
が同値であるとは、𝔪
と
𝔪′
の公倍数であるような
𝔪′′
が存在して
I𝔪′′ → I𝔪/H
の核と
I𝔪′′ → I𝔪′/H′
の核が等しいことと定義する。この同値関係による合同群の同値類とアーベル拡大の対応は一対一になる[20]。イデールによる定式化ではこの対応がより直接的に記述される。
導手
編集L/K を代数体の有限次アーベル拡大とする。アルティン相互法則が成り立つような2つのモジュラスの最大公約数でもアルティン相互法則が成り立つ。したがってアルティン相互法則が成り立つ最小のモジュラスが存在する。このモジュラスを導手（英: conductor、独: führer）と呼び、記号では 𝔣L/K と表す[10]。
判別公式
編集
L/K
を代数体の有限次アーベル拡大、𝔪 をこの拡大に対してアルティン相互法則が成り立つようなモジュラスとする。このとき、相対判別式
disc(L/K)
と導手を関係づける公式
が知られている。ここで
χ
は
I𝔪/H𝔪
の指標をすべてわたり、𝔣χ
は合同群
Ker χ
に対応するアーベル拡大の導手、𝔣χ, 0
はその有限部分である。これはハッセの判別公式︵独: Führerdiskriminantenproduktformel︶と呼ばれている[20][21]。
が知られている。ここで
χ
は
I𝔪/H𝔪
の指標をすべてわたり、𝔣χ
は合同群
Ker χ
に対応するアーベル拡大の導手、𝔣χ, 0
はその有限部分である。これはハッセの判別公式︵独: Führerdiskriminantenproduktformel︶と呼ばれている[20][21]。
射類体
編集詳細は「射類体」を参照
任意のモジュラス
𝔪
に対して存在定理より
H = P𝔪
に対応するアーベル拡大体が存在する。この拡大体は
𝔪
によって決まるので
K𝔪
で表す。この体は射類体と呼ばれている。
射類体の導手
𝔣K𝔪/K
は
𝔪
を割るが一致するとは限らない。例えば有理数体のモジュラス
𝔪 = (2)
に対する射類体は有理数体に一致するので導手は
𝔣 = (1)
である。またこの例から分かるように異なるモジュラスに対する射類体が等しくなるということもある。
不分岐類体論
編集詳細は「ヒルベルト類体」を参照
代数体
K
の自明なモジュラス
𝔪 = (1)
を取り
H = P(1) と置く。存在定理よりこれに対応するアーベル拡大
K′
が存在する。これを
K
上のヒルベルト類体、または絶対類体︵absolute class field︶と呼ぶ[22]。射類体の記号を使えば、これを
K(1)
と表すこともできる。もともとヒルベルトが存在を予想した﹁類体﹂は無限素点で何も条件をつけていないのでこの体とは異なる。しかし、現在ヒルベルト類体と呼ばれているものはここで定義したものである[23]。
アルティン相互法則により次が成り立つ。
●ヒルベルト類体のもとの代数体上のガロア群はイデアル類群と同型である。またその同型写像はアルティン写像により与えられる。
●代数体のすべての素イデアルはヒルベルト類体において不分岐である。さらに、素イデアルが定めるイデアル類群の元の位数とヒルベルト類体における剰余次数は等しい。
ヒルベルト類体はすべての射類体に含まれる。代数体のすべてのイデアルはヒルベルト類体に延長すると単項イデアルになることが知られている︵単項化定理︶。
終結定理
編集
類体論は、有限次アーベル拡大
L/K
に対してイデアルのノルムの成す群
N𝔪(L/K)
に
P𝔪
を乗じた群、つまり拡大に対する合同群
H𝔪(L/K)
を考えることでアーベル体に対して深い理解をもたらした。しかし、この手法は非アーベル拡大には通じない。このことを端的に示すのが次の終結定理である。
終結定理 L/K を任意の有限次拡大とする。このとき、この拡大に対する合同群 H𝔪(L/K) は Lに含まれる最大アーベル拡大に対する合同群に等しい[24]。
言い換えると、体拡大に対する合同群からは、含まれているアーベル拡大についての情報しか得られない。類体論に主要な貢献をなした高木は、この定理を提示したのち、﹁合同類別を以てしては、その統制力は直接には k上の﹁アアベル﹂体以上には及び得ない。それ以上、類体論の拡張は将来の発展にまたねばならない﹂という言葉で自著﹃代数的整数論 : 一般論及類体論﹄を締めくくった[25]。その後の発展については#類体論の一般化参照。
イデールを使った定式化
編集
イデアルの言葉による類体論は、具体的であり、多くの場合に最も便利である[26]。しかし、モジュラス
𝔪
を固定するため一度に取り扱えるのは導手が
𝔪
を割る有限次アーベル拡大だけであったり、また無限次アーベル拡大が扱えないなどの短所もある。イデールの言葉による類体論では、無限次拡大も扱え、すべてのアーベル拡大を同時に取り扱える。
K
を大域体、つまり代数体もしくは有限体上の1変数代数関数体とし、そのイデール群を
JK、イデール類群を
CK、最大アーベル拡大を Kabと表す[注釈4]。このとき、大域アルティン写像︵global Artin map︶[注釈5]、または大域相互律写像︵global reciprocity map︶[27]、標準射︵canonical morphism︶[28]などと呼ばれる準同型
が存在して、次を満たす。
局所と大域
K の任意の素点 vに対し、次の図式
は可換図式[29][30]。ここで、(1) の写像は局所類体論で定義される局所アルティン写像、(2) は作用の制限から得られる写像、(3) は φK、(4) は K×
v の元 xを v成分は xでその他の成分は1のイデールに送る写像である。
相互法則
主イデールは φK の核に含まれる[31]。つまり
が成り立つ。また任意の有限次アーベル拡大 L/K に対して φK から自然に同型
が誘導される。ここで NL/F はイデール類群のノルム写像である。
存在定理
イデール類群 CKの任意の有限指数開部分群 Nに対して一意に定まる有限次アーベル拡大 L/K が存在して N= NL/K(CL) が成り立つ[31]。
相互法則と存在定理から、Gal(Kab/K) と、CK の有限指数開部分群についての副有限完備化は同型になる[32]。そして Kの有限次アーベル拡大とイデール類群 CKの有限指数開部分群の間に1対1の対応
{ Kの有限次アーベル拡大 } ∋ L↦ NL/KCL ∈ { CKの有限指数開部分群 }
が存在することがわかる[31]。
考えている大域体 Kが代数体の場合には、φK は全射であり、その核は単位元の連結成分 DKであるため、
であることが示される[32]。そして、無限次アーベル拡大の場合に1対1対応
{ Kの有限次とは限らないアーベル拡大 } ∋ L↦ NL/KCL ∈ { CKの単位元の連結成分を含む閉部分群 }
が成り立つ[33][34]。
考えている大域体 Kが有限体上の1変数代数関数体の場合には、φK は全射とは限らないが、その像は稠密であり、単射である[35]。
が存在して、次を満たす。
局所と大域
K の任意の素点 vに対し、次の図式
は可換図式[29][30]。ここで、(1) の写像は局所類体論で定義される局所アルティン写像、(2) は作用の制限から得られる写像、(3) は φK、(4) は K×
v の元 xを v成分は xでその他の成分は1のイデールに送る写像である。
相互法則
主イデールは φK の核に含まれる[31]。つまり
が成り立つ。また任意の有限次アーベル拡大 L/K に対して φK から自然に同型
が誘導される。ここで NL/F はイデール類群のノルム写像である。
存在定理
イデール類群 CKの任意の有限指数開部分群 Nに対して一意に定まる有限次アーベル拡大 L/K が存在して N= NL/K(CL) が成り立つ[31]。
相互法則と存在定理から、Gal(Kab/K) と、CK の有限指数開部分群についての副有限完備化は同型になる[32]。そして Kの有限次アーベル拡大とイデール類群 CKの有限指数開部分群の間に1対1の対応
{ Kの有限次アーベル拡大 } ∋ L↦ NL/KCL ∈ { CKの有限指数開部分群 }
が存在することがわかる[31]。
考えている大域体 Kが代数体の場合には、φK は全射であり、その核は単位元の連結成分 DKであるため、
であることが示される[32]。そして、無限次アーベル拡大の場合に1対1対応
{ Kの有限次とは限らないアーベル拡大 } ∋ L↦ NL/KCL ∈ { CKの単位元の連結成分を含む閉部分群 }
が成り立つ[33][34]。
考えている大域体 Kが有限体上の1変数代数関数体の場合には、φK は全射とは限らないが、その像は稠密であり、単射である[35]。
ガロア・コホモロジーを使った定式化
編集
ガロア・コホモロジーを使う文脈では、類体論の相互法則は次のように述べられる︵ブラウアー群も参照︶。
K を有限次代数体、L を Kの有限次ガロア拡大︵アーベルでなくともよい︶とする。L
のイデール類群
CL
にはガロア群
Gal(L/K)
が作用するので、CL をガロア加群と見て群のコホモロジーを取ったものを
Hq(Gal(L/K), CL)
と書く︵q は任意の整数、定義については Neukirch (2015, p. 15) を参照︶。このとき、invariant map︵直訳: 不変量写像︶と呼ばれる同型写像
![{\displaystyle \mathrm {inv} _{L/K}:H^{2}(\mathrm {Gal} (L/K),C_{L}){\stackrel {\simeq }{\to }}{\tfrac {1}{[L:K]}}\mathbb {Z} /\mathbb {Z} }](https://wikimedia.org/api/rest_v1/media/math/render/svg/7012435d87b0a48245d26867a0b408a1e5ee3dfe)
が存在する[36]。この同型によって
1/[L : K]
が定める右側の群の元に対応する左側の
H2(Gal(L/K), CL)
の元を
uL/K
と書く。これを基本類︵fundamental class︶という[37]。任意の整数 qに対して、基本類のカップ積が定める写像
は同型写像になる[37]。この同型の q= −2 の場合を考えることにより、アルティン相互法則と呼ばれる同型
が得られる[37]。ここで
Gal(L/K)ab
は
Gal(L/K)
の最大アーベル商︵アーベル化︶である。この写像は相互律写像︵reciprocity map︶[37]、または中山正にちなんで中山写像︵Nakayama map︶[38][39]と呼ばれている。この同型写像の逆写像から得られる写像
をノルム剰余記号︵norm residue symbol︶という[37]。以上から、有限次ガロア拡大 L/K に対して完全系列
が存在することがわかる。これがガロア・コホモロジーの文脈で述べられる類体論の相互法則である。
なお、L
や
K
が局所体の場合にも、イデール類群
CL
を
L
の乗法群
L×
に置き換えれば同様のことが成り立つ[40]。局所体の場合と大域体の場合をまとめて扱えるように、共通する上述の性質を抽象化したものが類構造である[41]。
コホモロジーを用いずに非常に明示的で応用が利く方法などもある[要説明]。
が存在する[36]。この同型によって
1/[L : K]
が定める右側の群の元に対応する左側の
H2(Gal(L/K), CL)
の元を
uL/K
と書く。これを基本類︵fundamental class︶という[37]。任意の整数 qに対して、基本類のカップ積が定める写像
は同型写像になる[37]。この同型の q= −2 の場合を考えることにより、アルティン相互法則と呼ばれる同型
が得られる[37]。ここで
Gal(L/K)ab
は
Gal(L/K)
の最大アーベル商︵アーベル化︶である。この写像は相互律写像︵reciprocity map︶[37]、または中山正にちなんで中山写像︵Nakayama map︶[38][39]と呼ばれている。この同型写像の逆写像から得られる写像
をノルム剰余記号︵norm residue symbol︶という[37]。以上から、有限次ガロア拡大 L/K に対して完全系列
が存在することがわかる。これがガロア・コホモロジーの文脈で述べられる類体論の相互法則である。
なお、L
や
K
が局所体の場合にも、イデール類群
CL
を
L
の乗法群
L×
に置き換えれば同様のことが成り立つ[40]。局所体の場合と大域体の場合をまとめて扱えるように、共通する上述の性質を抽象化したものが類構造である[41]。
コホモロジーを用いずに非常に明示的で応用が利く方法などもある[要説明]。
各種特別な体に関する類体論
編集
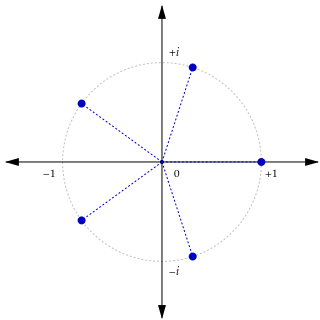
幾つかの小さい体、例えば有理数体 Qやその虚二次拡大体については、もっとたくさんの情報が得られる詳細な理論が存在する。例えば、Q の絶対ガロア群のアーベル化 Gは、全ての素数に亙って取った p-進整数環の単元群の無限直積︵に自然同型︶であり、対応する Qの最大アーベル拡大は1の冪根全てによって生成された体となる。このことは、もとはレオポルト・クロネッカーの予想であったクロネッカー–ヴェーバーの定理として知られる。この場合の、類体論の相互律同型︵あるいはアルティンの相互律写像︶も同定理に従って具体的に書くことができる。1の全ての冪根からなる群を
と書くことにする︵円周群 C× のねじれ部分群︶と、アルティンの相互律写像はそれが数論的正規化されているならば
によって、あるいはそれが幾何学的正規化されているならば
によって与えられる。しかし、このような小さな代数体に対する詳細理論の主要な構成法は一般の代数体の場合にまで拡張することはできないし、一般類体論で用いられるのはもっと違った概念的原理である。
と書くことにする︵円周群 C× のねじれ部分群︶と、アルティンの相互律写像はそれが数論的正規化されているならば
によって、あるいはそれが幾何学的正規化されているならば
によって与えられる。しかし、このような小さな代数体に対する詳細理論の主要な構成法は一般の代数体の場合にまで拡張することはできないし、一般類体論で用いられるのはもっと違った概念的原理である。
類体論の一般化
編集
3つの主要な一般化があり、それぞれが非常に興味深い。 ラングランズ・プログラム、遠アーベル幾何学、および高次類体論である。
数論における一つの自然な展開は、大域体の︵アーベルとは限らない︶一般のガロワ拡大に対する情報を与える非可換類体論の構成と理解を行うことである。ラングランズ対応が非可換類体論と見做されることが多く、そして実際にラングランズ対応が確立されたときには大域体の非可換ガロワ拡大に関する非常に豊かな理論を含むことになるのだが、しかしラングランズ対応はアーベル拡大の場合の類体論が持っていた有限次ガロワ拡大についての数論的情報のほとんどを含んでいないのである。しかもラングランズ対応は類体論の存在定理に対応するものも含んでいない、即ち、ラングランズ対応における類体の概念は存在しないのである。局所および大域の非可換類体論はいくつか存在し、それらはラングランズ対応の観点に対する別の選択肢を与えてくれる。
類体論のもう1つの一般化は遠アーベル幾何学であり、完全な絶対ガロア群または代数的基本群(Algebraic fundamental group)の情報から元のオブジェクト︵たとえば、数体またはその上の双曲線︶を復元するアルゴリズムを研究するものである。[42] [43]
もう1つ、数論幾何における自然な展開は、高次局所体および高次大域体のアーベル拡大を構成及び理解することである。後者の高次大域体は、整数環上の有限型スキームの函数体およびその適当な局所化や完備化として生じる。﹁高次局所および大域類体論﹂は代数的 K-理論や、一次元類体論で用いられる K1の代わりに適当なミルナー K-群を用いる。高次局所および大域類体論は、A. パーシン、加藤和也、イヴァン・フェセンコ、スペンサー・ブロック、斎藤秀司らの数学者が展開した。代数的 K-理論を用いずに高次大域類体論を展開しようとする試みもある (G. Wiesend) が、このやり方は高次局所類体論を含むものではなく、また局所理論と大域理論との間に互換性がない。
歴史
編集詳細は「類体論の年表」を参照
類体論の起源はガウスによって与えられた平方剰余の相互律にある。それが一般化されるまでには長きに亙る歴史的な取り組み、たとえば二次形式とその﹁種の理論﹂(Genus of a quadratic form)、クンマー・クロネッカー・ヘンゼルなどのイデアルおよび完備化に関する業績、円分体およびクンマー拡大の理論などがあった。
最初の二つの類体論は、非常にはっきりした円分類体論と虚数乗法類体論である。これらは付加的な構造︵有理数体の場合には1の冪根、有理数体の虚二次拡大体の場合には楕円曲線が虚数乗法を持つことと位数有限であること︶が利用できる。随分後になって、志村の理論は代数的数体のクラスに対する非常に明示的な新たな類体論を与えた。これらは基礎体の具体的な構造を非常に陽に用いる理論であって、勝手な数体に対してもうまくいくように拡張することはできない。正標数 pの体に関しては、河田と佐武がヴィット双対性を用いて相互律準同型の p-成分の非常に平易な記述を得ている。
しかし、一般類体論はこういったものとは異なる概念を用い、その構成法が任意の大域体に対してうまく機能するようにしなければならない。
大きな転機となったのは1898年ヒルベルトが︵狭義の︶ヒルベルト類体の存在と性質を予想したことである。また彼の提起した有名な問題が更なる発展の刺激となって、高木貞治、フィリップ・フルトヴェングラー、エミール・アルティン、ヘルムート・ハッセほか多数による種々の相互律が導かれることとなった。著しく重要な高木の存在定理が1920年に知られ、全ての主要な結果は1930年ごろまでには出そろっていた。証明されるべき古典的な予想の最後の一つは単項化定理であった。類体論の最初の証明には、頑強な解析学的手法が用いられた。1930年代以降は、無限次元拡大とそのガロワ群に関するヴォルフガンク・クルルの理論が有効であることが次第に認められていく。この理論はポントリャーギン双対性と結びついて、中心的な結果であるアルティンの相互律のより抽象的な定式化が分かり易くなった。重要な段階は、1930年代にクロード・シュヴァレーによってイデールが導入されたことである。イデールをイデアル類の代わりに用いることで、大域体のアーベル拡大を記述する構造は本質的に明確化および単純化され、中心的な結果のほとんどが1940年までに証明された。
この結果の後には、群コホモロジーの言葉を使った定式化がなされ、それが何世代かの数論学者が類体論を学ぶ際の標準となったが、コホモロジーを用いる方法の難点の一つは、それがあまり具体的でないことである。ベルナルド・ドワーク、ジョン・テイト、ミッシェル・ハゼウィンケルによる局所理論への貢献、およびユルゲン・ノイキルヒによる局所および大域理論の再解釈の結果として、あるいは多くの数学者による明示的な相互公式に関する業績と関連して、1990年代にはコホモロジーを用いない非常に明確な類体論の表現が確立された。このあたりの詳細は、例えばノイキルヒの本を参照せよ。
脚注
編集注釈
編集
(一)^
無限素点は、それが実素点であり、実素点の上にある素点がすべて実素点であるとき分解するという。それ以外のとき分岐するという(Milne (2020, p. 4))。
(二)^
射︵ray︶という言葉はドイツ語のStrahlから来ている。高木 (1971, p. 149)
によれば、かつてFueterが﹁数の乗法群﹂の意味でStrahlの語を使ったという。高木は﹁fantasticな造語の邦訳﹂を避け、Strahlは日本語に訳さず記号表記で通している。
(三)^
狭くなるのは類であって、群としては大きくなる。そのため
Milne (2020, p. 5)
では﹁narrow-class group﹂と﹁narrow﹂と﹁class﹂をハイフンで結合した表記を使っている。また、﹁狭義﹂は﹁narrow sense﹂の訳語として使われることが多いこと、狭義類群は一般化されたイデアル類群、つまり広義のイデアル類群の一種であることから、﹁狭義類群﹂という訳語は混乱を生じさせやすく、注意が必要である。
(四)^
記号は主として Cassels & Fröhlich (1967, p. 173) に従い、定理の述べ方は主として Milne (2020) に従う。
(五)^
Milne (2020, p. 180, Remark 5.8) でそう呼んでいる。
出典
編集- ^ a b c Conrad, p. 8.
- ^ 高木 1971, p. 148。ここでは約数、倍数、最大公約数、最小公倍数しか定義されていないが、その他の用語も通常の整数やイデアルにおけるものを準用する。
- ^ Milne 2020, p. 149.
- ^ Neukirch 2015, p. 113.
- ^ 高木 1971, p. 151; Milne 2020, p. 158.
- ^ a b Milne 2020, p. 157.
- ^ Conrad, p. 9; 加塩 2015, p. 30.
- ^ a b Conrad, p. 15.
- ^ Conrad, p. 10.
- ^ a b Conrad, p. 9.
- ^ 高木 1971, 序文.
- ^ 高木 1971, p. 174.
- ^ a b 高木 1971, p. 246.
- ^ a b 高木 1971, p. 196.
- ^ Conrad.
- ^ Gras 2005, p. 144.
- ^ 高木 1971, p. 142.
- ^ Neukirch 2015, p. 174.
- ^ 高木 1971, p. 150.
- ^ a b Conrad, p. 12.
- ^ 高木 1971, p. 237.
- ^ Neukirch 2015, p. 166.
- ^ Conrad, p. 7.
- ^ 高木 1971, p. 246; Milne 2020, p. 161. 定理の表現の仕方はMilneにあわせている。
- ^ 高木 1971, p. 247.
- ^ Milne 2020, p. 177.
- ^ Gras 2005, p. 104.
- ^ Weil 1995, p. 275.
- ^ Weil 1995, pp. 277-278.
- ^ Weil 1995, p. 245, Proposition 2.
- ^ a b c Milne 2020, p. 179.
- ^ a b Cassels & Fröhlich 1967, p. 173.
- ^ Lang 1994, p. 212.
- ^ Gras 2005, p. 123.
- ^ Milne 2020, p. 180.
- ^ Neukirch 2015, p. 150.
- ^ a b c d e Neukirch 2015, p. 152.
- ^ Neukirch 2015, p. 70.
- ^ Koch 2001, p. 90.
- ^ Neukirch 2015, p. 91-93.
- ^ Cassels & Fröhlich 1967, p. 178.
- ^ Fesenko, Ivan (2015), Arithmetic deformation theory via arithmetic fundamental groups and nonarchimedean theta functions, notes on the work of Shinichi Mochizuki, Eur. J. Math., 2015
- ^ Fesenko, Ivan (2021), Class field theory, its three main generalisations, and applications, May 2021, EMS Surveys 8(2021) 107-133
参考文献
編集- Artin, Emil; Tate, John (1990), Class field theory, Redwood City, Calif.: Addison-Wesley, ISBN 978-0-201-51011-9
- Cohen, Henri; Stevenhagen, Peter (2008), “Computational class field theory”, in Buhler, J.P.; P., Stevenhagen, Algorithmic Number Theory: Lattices, Number Fields, Curves and Cryptography, MSRI Publications, 44, Cambridge University Press, pp. 497–534, ISBN 978-0-521-20833-8, Zbl 1177.11095
- Cassels, J.W.S.; Fröhlich, Albrecht, eds. (1967), Algebraic Number Theory, Academic Press, Zbl 0153.07403
- Iwasawa, Kenkichi (1986), Local class field theory, Oxford Mathematical Monographs, The Clarendon Press Oxford University Press, ISBN 978-0-19-504030-2, MR863740, Zbl 0604.12014
- Neukirch, Jürgen (1986), Class Field Theory, Berlin, New York: Springer-Verlag, ISBN 978-3-540-15251-4
- Neukirch, Jürgen (2015) (PDF). Class Field Theory (Free Online Edition)
- Neukirch, Jürgen (1999), Algebraic Number Theory, Grundlehren der mathematischen Wissenschaften, 322, Berlin: Springer-Verlag, ISBN 978-3-540-65399-8, Zbl 0956.11021, MR1697859
- Kawada, Y. (1955), “Class formations”, Duke Math.J. 22: 165–177, Zbl 0067.01904
- Kawada, Y.; Satake, I. (1956), “Class formations. II”, J.Fac. Sci.Univ. Tokyo Sect. 1A 7: 353–389, Zbl 0101.02902
- Conrad, Keith, History of class field theory.
- Gras, Georges (second corrected printing 2005), Class field theory: From theory to practice, New York: Springer
- Milne, J.S. (2020). Class Field Theory (v4.03)
- 高木貞治『代数的整数論 : 一般論及類体論 第2版』岩波書店、1971年。ISBN 9784000056304。
- 加塩朋和 (2015年). “代数学特論１”. 2022年6月1日閲覧。
- Koch, Helmut (2001). “The History of the Theorem of Shafarevich in the Theory of Class Formations”. Class Field Theory – Its Centenary and Prospect: 87–106. doi:10.2969/aspm/03010087.
- Weil, André (1995). Basic number theory. Springer-Verlag. ISBN 978-3-540-58655-5