随伴関手
表示
(左随伴から転送)
数学の特に圏論における随伴︵ずいはん、英: adjunction︶とは、二つの関手の間の︵ある種の双対的な︶関係のことである︵随伴関係にある関手を持つ関手もあれば、持たない関手もある︶。直感的に言えば、二つの相互に関連する圏の間に認められる、弱い同値的な関係のことである。この関係を表す関手のペアを随伴関手と呼び、片方を左随伴、もう片方を右随伴と呼ぶ。随伴の概念・随伴関手のペアは数学に遍在し、最適化や効率に関する直観的概念を明らかにし、また、ある種の数学的問題の"解決法の最適化"を行う過程で見出される(代数における集合上の自由群の構成や、位相空間におけるStone–Čech compactification(英語版)の構成などがその例である。
圏  と
と  の間の随伴とは、二つの関手
の間の随伴とは、二つの関手
 の対であって、圏
の対であって、圏  の任意の対象 X、圏
の任意の対象 X、圏  の任意の対象 Yに対して、集合の全単射
の任意の対象 Yに対して、集合の全単射
 が存在して、これが Xと Yについて自然となるものを言う。このとき、関手 Fを左随伴函手と呼び、他方 Gを右随伴函手と呼ぶ。また、﹁F は Gの左随伴である﹂ (同じことだが、﹁G は Fの右随伴である﹂)という関係を
が存在して、これが Xと Yについて自然となるものを言う。このとき、関手 Fを左随伴函手と呼び、他方 Gを右随伴函手と呼ぶ。また、﹁F は Gの左随伴である﹂ (同じことだが、﹁G は Fの右随伴である﹂)という関係を
 と書く。
と書く。
 と
と  の間の随伴とは、二つの関手
の間の随伴とは、二つの関手
 の対であって、圏
の対であって、圏  の任意の対象 X、圏
の任意の対象 X、圏  の任意の対象 Yに対して、集合の全単射
の任意の対象 Yに対して、集合の全単射
 が存在して、これが Xと Yについて自然となるものを言う。このとき、関手 Fを左随伴函手と呼び、他方 Gを右随伴函手と呼ぶ。また、﹁F は Gの左随伴である﹂ (同じことだが、﹁G は Fの右随伴である﹂)という関係を
が存在して、これが Xと Yについて自然となるものを言う。このとき、関手 Fを左随伴函手と呼び、他方 Gを右随伴函手と呼ぶ。また、﹁F は Gの左随伴である﹂ (同じことだが、﹁G は Fの右随伴である﹂)という関係を
 と書く。
と書く。
導入
[編集]The slogan is “Adjoint functors arise everywhere.”
—Saunders Mac Lane、(Mac Lane 1998, p. vii)
この記事のたくさんの例ではよい数学的構造の多くが随伴関手であることを少しだけ紹介する。 このことは、左(右)随伴関手に関する一般的な定理、たとえば色々な定義のしかたの同値性や余極限(極限)を保存するという定理(このことは数学の全ての分野で見つかる)から、多くの役に立つ・非自明な結果を導くことが出来る。
綴り
[編集]
"adjunct"と"adjunction"と"adjoint"というように、二つの異なる語根が使われる(例えば、この記事の英語版)。Oxford shorter English dictionaryによると、"adjunct"はラテン語由来であり、"adjoint"はフランス語由来である。
Mac Lane 著 Categories for the working mathematician 第4章 "Adjoints" においては、次のように使われているのが確認できる。
 The hom-set bijection
The hom-set bijection  is an "adjunction".
If
is an "adjunction".
If an arrow in
an arrow in  ,
,  is the right "adjunct" of
is the right "adjunct" of  (p. 81).
The functor
(p. 81).
The functor  is left "adjoint" for
is left "adjoint" for  .
.
 The hom-set bijection
The hom-set bijection  is an "adjunction".
If
is an "adjunction".
If an arrow in
an arrow in  ,
,  is the right "adjunct" of
is the right "adjunct" of  (p. 81).
The functor
(p. 81).
The functor  is left "adjoint" for
is left "adjoint" for  .
.
動機
[編集]最適化問題の解として
[編集]
随伴関手は各種の問題に決まりきった方法を使ってもっとも効率的な解を与える方法といえる。たとえば、環論の初等的な問題として、非単位的環を環に変える問題がある。
もっとも効率的に行うには、'1'を追加し、環の公理で要求されている元(環の各元rに対するr+1等)を全て(そして最小限を)追加し、公理が要求する以上の関係は持たない新しい環を構成すればよい。さらに、この構成方法は本質的にはどの非単位的環についても同じやりかたになる。
曖昧にして示唆的であるが、圏論の言語によって次のように簡潔に表現できる。
﹁構成がもっとも効率的であるとは普遍的であること、決まりきったとは関手を定めることとする。﹂
ここで、普遍的であるということには﹁始﹂普遍的と﹁終﹂普遍的の2つの種類があり、これらは双対であるので、片方のみについて考えるだけで十分である。
﹁始﹂の場合の普遍性とは、問題を記述できる圏Eを準備して、構成したいものがEの始対象になるようにすることである。この方法の利点は、上限を求めることと同様に、最適化(ここでは、もっとも効率的な解を見つけること)が正確な結果を与え、認識しやすいことにある。正しいEを選ぶには少しこつがいる。たとえば、単位的でない環Rがあった場合に、圏Eの対象は非単位的環の準同型 R→ Sであって、Sが乗法的単位元をもつものであるする。対象 R→ S1と 対象R → S2の間の射は三角可換図式(R → S1,R → S2, S1→ S2)のうち、S1 → S2 が単位元を保存する環の準同型になっているとする。対象 R→ S1と 対象R → S2の間に射が存在するということは、S1 は少なくとも S2よりもより効率的な解であることを示している。すなわち、S2 は S1よりも多くの元を持っていたり、公理にない関係を満たすことが可能である。よって、R → R* が Eの始対象であるということは、始対象からはE の他のどの対象へも射が存在するということから、R* はもっとも効率的な解であることがいえる。
非単位的環を環に変えるこの方法がもっとも効率的で決まりきった方法であるということを、この方法が随伴関手を定めていると一言で表現することができる。
最適化問題の逆
[編集]
次に、関手Fから始めた場合では﹁Fがもっとも効率的な解となる問題は存在するのか?﹂という(曖昧な)質問が可能である。
FがG問題のもっとも効率的な解であるということは、ある意味では正確に、GがFが解となるもっとも難しい問題であることと同値となる。[要出典]
これが随伴関手が対となって現れることの直観的な解釈であり、実際これは正しいが、普遍射を使った定義では自明ではない。随伴関手を用いた対称形の随伴の定義(FはGの左随伴であると言ってもよいし、GはFの右随伴であると言ってもよい)を使うことで、このことが明示的になるという利点がある。
形式的な定義
[編集]
随伴関手の定義はさまざまな方法がある。これらの同値性は基本的な事実であるが自明ではないため非常に有用である。この記事ではいくつかの定義を与える。
●普遍射を用いた定義は書くのが簡単で、随伴関手を構成したり、随伴であることを証明する場合に必要な検証項目が少ない。最適化に対する直観にもっとも近い方法である。
●余単位-単位随伴を用いた定義は随伴関手であることが分かっている関手に関係する証明を書くのに便利である、なぜなら、直接操作できる公式を持つからである。
●hom集合を用いた定義はもっとも対称性がわかりやすい、これが随伴という単語を使う理由である。
随伴関手は数学の全ての分野に現れる。これらの定義が持つ構造を他の定義が持つ構造に持ち上げるためには長いが明らかな証明が必要であり、このことが随伴を完全に有用なものにしている。随伴の各定義を行き交うことは、各分野で繰り返し行われてきた退屈な部分を暗黙に使っていることになる。例えばcounitが終対象であり自然であることから全ての右随伴関手が極限を保存することを証明できる。
記法の約束
[編集]
随伴の理論は基礎付けに﹁左﹂と﹁右﹂という言葉を用い、また考えるべき二つの圏 𝒞 と 𝒟 の中にはたくさんの構成要素が存在している。そこで、﹁左﹂の圏 𝒞 からとったのか﹁右﹂の圏 𝒟 から取ったのかを、この左、右の順で付ける文字がアルファベット順となるようにし、またできうる限りこの順で書き下すようにすると非常に便利である。
この記事では例えば、X、F、f、ε は圏Cから、Y、G、g、η は圏Dから取ってくるものとする。そして、可能な場合は、この順で左から右に使うもとのする(例えば、関手 F:C←D はCから取ってきたものと考える)
普遍射による定義
[編集]
関手 F : C← Dが左随伴関手であるとは、Cの各対象Xに対して、FからXへの普遍射が存在することである。Cの各対象Xに関してDの対象G0XとFからXへの普遍射εX : F(G0X) → Xを決めると、関手G : C→ Dで、GX = G0Xと、任意のCの射f : X→ XʹについてεXʹ  FG(f) = f
FG(f) = f εXが成り立つものが一意的に存在する。このとき、FはGの左随伴であるという。
関手 G : C→ Dが右随伴関手であるとは、Dの各対象Yに対して、YからGへの普遍射が存在することである。Dの各対象Yに関してCの対象F0YとYからGへの普遍射ηY : Y→ G(F0Y)を決めると、関手F : C← Dで、FY = F0Yと、任意のDの射g : Y→ YʹについてGF(g)
εXが成り立つものが一意的に存在する。このとき、FはGの左随伴であるという。
関手 G : C→ Dが右随伴関手であるとは、Dの各対象Yに対して、YからGへの普遍射が存在することである。Dの各対象Yに関してCの対象F0YとYからGへの普遍射ηY : Y→ G(F0Y)を決めると、関手F : C← Dで、FY = F0Yと、任意のDの射g : Y→ YʹについてGF(g)  ηY = ηYʹ
ηY = ηYʹ  gが成り立つものが一意的に存在する。このとき、GはFの右随伴であるという。
注意
用語から分かるように、FがGの左随伴であることとGがFの右随伴であることが同値であることは正しい。これは下記の対称的な定義では明らかである。普遍射を用いた定義は、与えられた関手が左または右随伴関手であることだけを確かめたいときに、必要な証明が最小限となるため、しばしば有用である。また、普遍射を求めることは最適化問題を解くことと似ているため、直観的でもある。
gが成り立つものが一意的に存在する。このとき、GはFの右随伴であるという。
注意
用語から分かるように、FがGの左随伴であることとGがFの右随伴であることが同値であることは正しい。これは下記の対称的な定義では明らかである。普遍射を用いた定義は、与えられた関手が左または右随伴関手であることだけを確かめたいときに、必要な証明が最小限となるため、しばしば有用である。また、普遍射を求めることは最適化問題を解くことと似ているため、直観的でもある。
 FG(f) = f
FG(f) = f εXが成り立つものが一意的に存在する。このとき、FはGの左随伴であるという。
関手 G : C→ Dが右随伴関手であるとは、Dの各対象Yに対して、YからGへの普遍射が存在することである。Dの各対象Yに関してCの対象F0YとYからGへの普遍射ηY : Y→ G(F0Y)を決めると、関手F : C← Dで、FY = F0Yと、任意のDの射g : Y→ YʹについてGF(g)
εXが成り立つものが一意的に存在する。このとき、FはGの左随伴であるという。
関手 G : C→ Dが右随伴関手であるとは、Dの各対象Yに対して、YからGへの普遍射が存在することである。Dの各対象Yに関してCの対象F0YとYからGへの普遍射ηY : Y→ G(F0Y)を決めると、関手F : C← Dで、FY = F0Yと、任意のDの射g : Y→ YʹについてGF(g)  ηY = ηYʹ
ηY = ηYʹ  gが成り立つものが一意的に存在する。このとき、GはFの右随伴であるという。
注意
用語から分かるように、FがGの左随伴であることとGがFの右随伴であることが同値であることは正しい。これは下記の対称的な定義では明らかである。普遍射を用いた定義は、与えられた関手が左または右随伴関手であることだけを確かめたいときに、必要な証明が最小限となるため、しばしば有用である。また、普遍射を求めることは最適化問題を解くことと似ているため、直観的でもある。
gが成り立つものが一意的に存在する。このとき、GはFの右随伴であるという。
注意
用語から分かるように、FがGの左随伴であることとGがFの右随伴であることが同値であることは正しい。これは下記の対称的な定義では明らかである。普遍射を用いた定義は、与えられた関手が左または右随伴関手であることだけを確かめたいときに、必要な証明が最小限となるため、しばしば有用である。また、普遍射を求めることは最適化問題を解くことと似ているため、直観的でもある。
余単位-単位随伴による定義
[編集]
圏CとDの余単位-単位随伴は2つの関手 F : C← Dと G : C→ Dおよび2つの自然変換︵それぞれ、この随伴の余単位射および単位射と呼ばれる︶
 であって、これらの合成
であって、これらの合成

 がそれぞれ、FとG上の恒等変換1F and 1Gとなることをいい、これらの自然変換をそれぞれcounitとunitと呼ぶ。
このとき、 FはGの左随伴であり GはFの右随伴であるという。この関係を
がそれぞれ、FとG上の恒等変換1F and 1Gとなることをいい、これらの自然変換をそれぞれcounitとunitと呼ぶ。
このとき、 FはGの左随伴であり GはFの右随伴であるという。この関係を 、または単に
、または単に と書く。
(ε,η)に関する上の条件を等式で書くと、counit-unit恒等式と呼ばれる
と書く。
(ε,η)に関する上の条件を等式で書くと、counit-unit恒等式と呼ばれる
 となり、これはCの各対象XとDの各対象Yについて
となり、これはCの各対象XとDの各対象Yについて
 .
が成り立つことを意味する。
これらの等式は随伴関手を代数的に操作する証明を短くするのに有用である。対応するstring diaglamでの見た目から、これはときにジグザグ恒等式と呼ばれる。この等式を覚えるには、まず、無意味な等式
.
が成り立つことを意味する。
これらの等式は随伴関手を代数的に操作する証明を短くするのに有用である。対応するstring diaglamでの見た目から、これはときにジグザグ恒等式と呼ばれる。この等式を覚えるには、まず、無意味な等式 を書き下し、簡単なやり方で合成が正しく定義されるようにFとGを追加すればよい。
注: ここでのcounitの"co"という接頭辞は極限(limit)や余極限(colimit)での用法とは一貫していない。なぜなら、余極限は﹁始﹂普遍性を満たすのに対し、counitの定める射は﹁終﹂普遍性を満たすからである。これらの双対についても同様である。ここでのunitという用語はモナドからの借用であり、恒等射1をモノイドに埋め込むところから来ている。
を書き下し、簡単なやり方で合成が正しく定義されるようにFとGを追加すればよい。
注: ここでのcounitの"co"という接頭辞は極限(limit)や余極限(colimit)での用法とは一貫していない。なぜなら、余極限は﹁始﹂普遍性を満たすのに対し、counitの定める射は﹁終﹂普遍性を満たすからである。これらの双対についても同様である。ここでのunitという用語はモナドからの借用であり、恒等射1をモノイドに埋め込むところから来ている。
 であって、これらの合成
であって、これらの合成

 がそれぞれ、FとG上の恒等変換1F and 1Gとなることをいい、これらの自然変換をそれぞれcounitとunitと呼ぶ。
このとき、 FはGの左随伴であり GはFの右随伴であるという。この関係を
がそれぞれ、FとG上の恒等変換1F and 1Gとなることをいい、これらの自然変換をそれぞれcounitとunitと呼ぶ。
このとき、 FはGの左随伴であり GはFの右随伴であるという。この関係を 、または単に
、または単に と書く。
(ε,η)に関する上の条件を等式で書くと、counit-unit恒等式と呼ばれる
と書く。
(ε,η)に関する上の条件を等式で書くと、counit-unit恒等式と呼ばれる
 となり、これはCの各対象XとDの各対象Yについて
となり、これはCの各対象XとDの各対象Yについて
 .
が成り立つことを意味する。
これらの等式は随伴関手を代数的に操作する証明を短くするのに有用である。対応するstring diaglamでの見た目から、これはときにジグザグ恒等式と呼ばれる。この等式を覚えるには、まず、無意味な等式
.
が成り立つことを意味する。
これらの等式は随伴関手を代数的に操作する証明を短くするのに有用である。対応するstring diaglamでの見た目から、これはときにジグザグ恒等式と呼ばれる。この等式を覚えるには、まず、無意味な等式 を書き下し、簡単なやり方で合成が正しく定義されるようにFとGを追加すればよい。
注: ここでのcounitの"co"という接頭辞は極限(limit)や余極限(colimit)での用法とは一貫していない。なぜなら、余極限は﹁始﹂普遍性を満たすのに対し、counitの定める射は﹁終﹂普遍性を満たすからである。これらの双対についても同様である。ここでのunitという用語はモナドからの借用であり、恒等射1をモノイドに埋め込むところから来ている。
を書き下し、簡単なやり方で合成が正しく定義されるようにFとGを追加すればよい。
注: ここでのcounitの"co"という接頭辞は極限(limit)や余極限(colimit)での用法とは一貫していない。なぜなら、余極限は﹁始﹂普遍性を満たすのに対し、counitの定める射は﹁終﹂普遍性を満たすからである。これらの双対についても同様である。ここでのunitという用語はモナドからの借用であり、恒等射1をモノイドに埋め込むところから来ている。
hom集合随伴
[編集]
圏CとDの間のhom集合の随伴は2つの関手 F : C← Dと G : C→ Dおよび、自然同型
 のことをいう。これはCの各対象XとDの各対象Yで添え字付けられた全単射の族
のことをいう。これはCの各対象XとDの各対象Yで添え字付けられた全単射の族
 .
を定める。
このとき、 FはGの左随伴であり GはFの右随伴であるという。この関係を
.
を定める。
このとき、 FはGの左随伴であり GはFの右随伴であるという。この関係を 、または単に
、または単に と書く。
この定義は普遍射を使ったものより少し確認することが多くて、すぐに得られる結果は余単位-単位随伴より少なくなるという論理的な折衷になっている。明らかな対称性や他の定義の間の架け橋にることは有用である。
Φが自然同型であるというときは、homC(F–, –) と homD(–, G–) が関手であると考える必要がある。実際、これらはDop × CからSet(集合の圏)への双関手である。詳しくはHom関手の項目を参照せよ。明示的に書くと、Φの自然性というのは、全てのCの射 f : X→ X′と全てのDの射g : Y′ → Yについて、以下の図式が可換になることをいう。
と書く。
この定義は普遍射を使ったものより少し確認することが多くて、すぐに得られる結果は余単位-単位随伴より少なくなるという論理的な折衷になっている。明らかな対称性や他の定義の間の架け橋にることは有用である。
Φが自然同型であるというときは、homC(F–, –) と homD(–, G–) が関手であると考える必要がある。実際、これらはDop × CからSet(集合の圏)への双関手である。詳しくはHom関手の項目を参照せよ。明示的に書くと、Φの自然性というのは、全てのCの射 f : X→ X′と全てのDの射g : Y′ → Yについて、以下の図式が可換になることをいう。
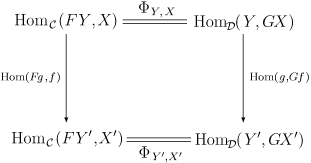
Naturality of Φ
この図式の縦方向の射はfやgを合成することで誘導される射である。
 のことをいう。これはCの各対象XとDの各対象Yで添え字付けられた全単射の族
のことをいう。これはCの各対象XとDの各対象Yで添え字付けられた全単射の族
 .
を定める。
このとき、 FはGの左随伴であり GはFの右随伴であるという。この関係を
.
を定める。
このとき、 FはGの左随伴であり GはFの右随伴であるという。この関係を 、または単に
、または単に と書く。
この定義は普遍射を使ったものより少し確認することが多くて、すぐに得られる結果は余単位-単位随伴より少なくなるという論理的な折衷になっている。明らかな対称性や他の定義の間の架け橋にることは有用である。
Φが自然同型であるというときは、homC(F–, –) と homD(–, G–) が関手であると考える必要がある。実際、これらはDop × CからSet(集合の圏)への双関手である。詳しくはHom関手の項目を参照せよ。明示的に書くと、Φの自然性というのは、全てのCの射 f : X→ X′と全てのDの射g : Y′ → Yについて、以下の図式が可換になることをいう。
と書く。
この定義は普遍射を使ったものより少し確認することが多くて、すぐに得られる結果は余単位-単位随伴より少なくなるという論理的な折衷になっている。明らかな対称性や他の定義の間の架け橋にることは有用である。
Φが自然同型であるというときは、homC(F–, –) と homD(–, G–) が関手であると考える必要がある。実際、これらはDop × CからSet(集合の圏)への双関手である。詳しくはHom関手の項目を参照せよ。明示的に書くと、Φの自然性というのは、全てのCの射 f : X→ X′と全てのDの射g : Y′ → Yについて、以下の図式が可換になることをいう。
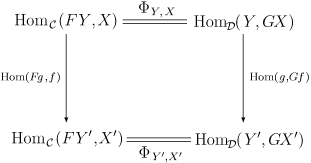
随伴の全容
[編集]
以上のことから、随伴にはたくさんの関手や自然変換を持っているが、その一部を決めるだけで他のものは決定される。
圏CとDの間の随伴は以下のものから構成される。
●左随伴と呼ばれる関手F : C← D
●右随伴と呼ばれる関手G : C→ D
●自然同型Φ : homC(F–,–) → homD(–,G–)
●余単位と呼ばれる自然変換 ε : FG→ 1C
●単位と呼ばれる自然変換 η : 1D → GF
等価な定式化として、XをCの任意の対象としYをDの任意の対象としたとき、
全てのCの射 に対して、Dの射
に対して、Dの射 で、以下の図式を可換にするものが唯一つ存在し、全てのDの射
で、以下の図式を可換にするものが唯一つ存在し、全てのDの射 に対して、Cの射
に対して、Cの射 で、以下の図式を可換にするものが唯一つ存在する
で、以下の図式を可換にするものが唯一つ存在する
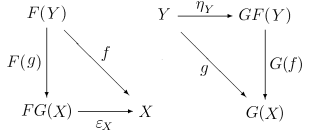 このことを使うと、以下に挙げる復元が可能である
●変換ε、η、Φは以下の等式で関連付けられる。
このことを使うと、以下に挙げる復元が可能である
●変換ε、η、Φは以下の等式で関連付けられる。
 ●変換ε、ηは余単位-単位恒等式を満たす
●変換ε、ηは余単位-単位恒等式を満たす
 ●Cにおいて、各対
●Cにおいて、各対 はFからXへの普遍射である
●Dにおいて、各対
はFからXへの普遍射である
●Dにおいて、各対 はYからGへの普遍射である
とくに、上記の等式によりΦ、ε、ηはこれらのうち1つを使って定めることができる。しかし、随伴関手FとGだけでは随伴を定めるには一般には十分ではない。以下では定義の同値性を解説する。
はYからGへの普遍射である
とくに、上記の等式によりΦ、ε、ηはこれらのうち1つを使って定めることができる。しかし、随伴関手FとGだけでは随伴を定めるには一般には十分ではない。以下では定義の同値性を解説する。
 に対して、Dの射
に対して、Dの射 で、以下の図式を可換にするものが唯一つ存在し、全てのDの射
で、以下の図式を可換にするものが唯一つ存在し、全てのDの射 に対して、Cの射
に対して、Cの射 で、以下の図式を可換にするものが唯一つ存在する
で、以下の図式を可換にするものが唯一つ存在する
 このことを使うと、以下に挙げる復元が可能である
●変換ε、η、Φは以下の等式で関連付けられる。
このことを使うと、以下に挙げる復元が可能である
●変換ε、η、Φは以下の等式で関連付けられる。
 ●変換ε、ηは余単位-単位恒等式を満たす
●変換ε、ηは余単位-単位恒等式を満たす
 ●Cにおいて、各対
●Cにおいて、各対 はFからXへの普遍射である
●Dにおいて、各対
はFからXへの普遍射である
●Dにおいて、各対 はYからGへの普遍射である
とくに、上記の等式によりΦ、ε、ηはこれらのうち1つを使って定めることができる。しかし、随伴関手FとGだけでは随伴を定めるには一般には十分ではない。以下では定義の同値性を解説する。
はYからGへの普遍射である
とくに、上記の等式によりΦ、ε、ηはこれらのうち1つを使って定めることができる。しかし、随伴関手FとGだけでは随伴を定めるには一般には十分ではない。以下では定義の同値性を解説する。
普遍射がhom集合随伴を導くこと
[編集]
普遍射の意味での右随伴関手 が与えられたとして、以下の手順を行う。
●関手
が与えられたとして、以下の手順を行う。
●関手 と自然変換
と自然変換 を構成する
●Dの各対象Yに対して、YからGへの普遍射
を構成する
●Dの各対象Yに対して、YからGへの普遍射 を選ぶ。すなわち、
を選ぶ。すなわち、 が得られ、対象関数Fと射の族
が得られ、対象関数Fと射の族 を得る
●各射
を得る
●各射 について、
について、 は普遍射であることから、
は普遍射であることから、 を通して
を通して を分解し、
を分解し、 を得る。これがFの射関数である
●分解についての可換図式から自然変換としての可換図式が得られる。よって、
を得る。これがFの射関数である
●分解についての可換図式から自然変換としての可換図式が得られる。よって、 は自然変換となる
●分解の一意性とGが関手であることから、Fの射関数が射の合成と恒等射を保存することがわかる
●自然同型
は自然変換となる
●分解の一意性とGが関手であることから、Fの射関数が射の合成と恒等射を保存することがわかる
●自然同型 を構成する
●Cの各対象XとDの各対象Yに対して、
を構成する
●Cの各対象XとDの各対象Yに対して、 は普遍射であることから、
は普遍射であることから、 は全単射となる。ここで、
は全単射となる。ここで、 とする
●
とする
● が自然変換で、Gが関手であることから、全てのCの対象
が自然変換で、Gが関手であることから、全てのCの対象 、
、 とDの対象
とDの対象 、
、 と全ての射
と全ての射 と
と に対して、
に対して、 であり、Φは両方の引数に関して自然である。
同様の議論により普遍射による左随伴関手の定義からhom集合の随伴を構成することができる。(右随伴を元に構成するほうが普通である。なぜなら、随伴対の右随伴を包含関手や忘却関手により自明なやり方で定めることが多くあるからである。)
であり、Φは両方の引数に関して自然である。
同様の議論により普遍射による左随伴関手の定義からhom集合の随伴を構成することができる。(右随伴を元に構成するほうが普通である。なぜなら、随伴対の右随伴を包含関手や忘却関手により自明なやり方で定めることが多くあるからである。)
 が与えられたとして、以下の手順を行う。
●関手
が与えられたとして、以下の手順を行う。
●関手 と自然変換
と自然変換 を構成する
●Dの各対象Yに対して、YからGへの普遍射
を構成する
●Dの各対象Yに対して、YからGへの普遍射 を選ぶ。すなわち、
を選ぶ。すなわち、 が得られ、対象関数Fと射の族
が得られ、対象関数Fと射の族 を得る
●各射
を得る
●各射 について、
について、 は普遍射であることから、
は普遍射であることから、 を通して
を通して を分解し、
を分解し、 を得る。これがFの射関数である
●分解についての可換図式から自然変換としての可換図式が得られる。よって、
を得る。これがFの射関数である
●分解についての可換図式から自然変換としての可換図式が得られる。よって、 は自然変換となる
●分解の一意性とGが関手であることから、Fの射関数が射の合成と恒等射を保存することがわかる
●自然同型
は自然変換となる
●分解の一意性とGが関手であることから、Fの射関数が射の合成と恒等射を保存することがわかる
●自然同型 を構成する
●Cの各対象XとDの各対象Yに対して、
を構成する
●Cの各対象XとDの各対象Yに対して、 は普遍射であることから、
は普遍射であることから、 は全単射となる。ここで、
は全単射となる。ここで、 とする
●
とする
● が自然変換で、Gが関手であることから、全てのCの対象
が自然変換で、Gが関手であることから、全てのCの対象 、
、 とDの対象
とDの対象 、
、 と全ての射
と全ての射 と
と に対して、
に対して、 であり、Φは両方の引数に関して自然である。
同様の議論により普遍射による左随伴関手の定義からhom集合の随伴を構成することができる。(右随伴を元に構成するほうが普通である。なぜなら、随伴対の右随伴を包含関手や忘却関手により自明なやり方で定めることが多くあるからである。)
であり、Φは両方の引数に関して自然である。
同様の議論により普遍射による左随伴関手の定義からhom集合の随伴を構成することができる。(右随伴を元に構成するほうが普通である。なぜなら、随伴対の右随伴を包含関手や忘却関手により自明なやり方で定めることが多くあるからである。)
余単位-単位随伴がhom集合随伴を導くこと
[編集]
関手  と
と  およびcounit-unit随伴
およびcounit-unit随伴 が与えられたとして、hom集合の随伴
が与えられたとして、hom集合の随伴
 を以下の手順で構成する。
●射
を以下の手順で構成する。
●射  と
と  に対して、
に対して、
 と定めると、ηとεが自然であるため、ΦとΨも自然である。
●Fが関手であることと、εが自然であることcounit-unit恒等式
と定めると、ηとεが自然であるため、ΦとΨも自然である。
●Fが関手であることと、εが自然であることcounit-unit恒等式 を順番に使って、
を順番に使って、
 を得る。よって、ΨΦは恒等変換である
●双対的に、Gが関手であること、ηが自然であることcounit-unit恒等式
を得る。よって、ΨΦは恒等変換である
●双対的に、Gが関手であること、ηが自然であることcounit-unit恒等式 を順番に使って、
を順番に使って、
 を得る。よって、ΦΨは恒等変換であり、Φ−1 = Ψを逆写像としてΦは自然同型となる。
を得る。よって、ΦΨは恒等変換であり、Φ−1 = Ψを逆写像としてΦは自然同型となる。
 と
と  およびcounit-unit随伴
およびcounit-unit随伴 が与えられたとして、hom集合の随伴
が与えられたとして、hom集合の随伴
 を以下の手順で構成する。
●射
を以下の手順で構成する。
●射  と
と  に対して、
に対して、
 と定めると、ηとεが自然であるため、ΦとΨも自然である。
●Fが関手であることと、εが自然であることcounit-unit恒等式
と定めると、ηとεが自然であるため、ΦとΨも自然である。
●Fが関手であることと、εが自然であることcounit-unit恒等式 を順番に使って、
を順番に使って、
 を得る。よって、ΨΦは恒等変換である
●双対的に、Gが関手であること、ηが自然であることcounit-unit恒等式
を得る。よって、ΨΦは恒等変換である
●双対的に、Gが関手であること、ηが自然であることcounit-unit恒等式 を順番に使って、
を順番に使って、
 を得る。よって、ΦΨは恒等変換であり、Φ−1 = Ψを逆写像としてΦは自然同型となる。
を得る。よって、ΦΨは恒等変換であり、Φ−1 = Ψを逆写像としてΦは自然同型となる。
hom集合随伴が上の全てを導くこと
[編集]
関手  と
と  および、hom集合の随伴
および、hom集合の随伴  が与えられたとして、普遍射の族を導くcounit-unit随伴
が与えられたとして、普遍射の族を導くcounit-unit随伴
 ,
を以下の手順で構成する。
●Cの各対象Xに対して、
,
を以下の手順で構成する。
●Cの各対象Xに対して、 とする。ここで、
とする。ここで、 は恒等射である。
●Dの各対象Yに対して、
は恒等射である。
●Dの各対象Yに対して、 とする。ここで、
とする。ここで、 は恒等射である。
●Φが全単射で自然であることから、各
は恒等射である。
●Φが全単射で自然であることから、各 はFからXへの普遍射であり、各
はFからXへの普遍射であり、各 はYからGへの普遍射である。
●Φが自然であることから、εとηの普遍性が導かれ、各射 f: FY→ Xと g: Y→ GXに対して、2つの公式
はYからGへの普遍射である。
●Φが自然であることから、εとηの普遍性が導かれ、各射 f: FY→ Xと g: Y→ GXに対して、2つの公式
 が成立する(これはΦを完全に決定する)
●二番目の公式のXにFYを代入し、gに
が成立する(これはΦを完全に決定する)
●二番目の公式のXにFYを代入し、gに を代入することで、1つ目のcounit-unit恒等式
を代入することで、1つ目のcounit-unit恒等式
 ,
を得る。一番目の公式のYにGXを代入し、fに
,
を得る。一番目の公式のYにGXを代入し、fに を代入することで、2つ目のcounit-unit恒等式
を代入することで、2つ目のcounit-unit恒等式
 を得る
を得る
 と
と  および、hom集合の随伴
および、hom集合の随伴  が与えられたとして、普遍射の族を導くcounit-unit随伴
が与えられたとして、普遍射の族を導くcounit-unit随伴
 ,
を以下の手順で構成する。
●Cの各対象Xに対して、
,
を以下の手順で構成する。
●Cの各対象Xに対して、 とする。ここで、
とする。ここで、 は恒等射である。
●Dの各対象Yに対して、
は恒等射である。
●Dの各対象Yに対して、 とする。ここで、
とする。ここで、 は恒等射である。
●Φが全単射で自然であることから、各
は恒等射である。
●Φが全単射で自然であることから、各 はFからXへの普遍射であり、各
はFからXへの普遍射であり、各 はYからGへの普遍射である。
●Φが自然であることから、εとηの普遍性が導かれ、各射 f: FY→ Xと g: Y→ GXに対して、2つの公式
はYからGへの普遍射である。
●Φが自然であることから、εとηの普遍性が導かれ、各射 f: FY→ Xと g: Y→ GXに対して、2つの公式
 が成立する(これはΦを完全に決定する)
●二番目の公式のXにFYを代入し、gに
が成立する(これはΦを完全に決定する)
●二番目の公式のXにFYを代入し、gに を代入することで、1つ目のcounit-unit恒等式
を代入することで、1つ目のcounit-unit恒等式
 ,
を得る。一番目の公式のYにGXを代入し、fに
,
を得る。一番目の公式のYにGXを代入し、fに を代入することで、2つ目のcounit-unit恒等式
を代入することで、2つ目のcounit-unit恒等式
 を得る
を得る
歴史
[編集]随伴の遍在性
[編集]
随伴関手の考えはダニエル・カンによって1958年に定式化された。多くの圏論の概念と同様に、ホモロジー代数において計算を行おうとした際に必要になったために導入された。この問題のきれいで系統的な表現を与えようと向き合った人々はアーベル群の圏において
hom(F(X), Y) = hom(X, G(Y))
のような関係があることに気づいていた。ここで、Fは関手 (つまり、Aとテンソル積を取る)であり、Gは関手hom(A,–)である。ここで等号を使うのは記号の乱用である。これらの群は実際には等しくないが、等しく見せるような自然な方法がある。自然に感じられる理由として、一番に、元々はこれらがX × AからYへの双線形写像の2つの異なった表現であるからである。しかし、これはテンソル積に関するいくぶん固有な話である。圏論においての全単射の自然性は自然同型の概念が元になっている。
この用語はヒルベルト空間において、上記のhom集合の間の関係と似た関係
(つまり、Aとテンソル積を取る)であり、Gは関手hom(A,–)である。ここで等号を使うのは記号の乱用である。これらの群は実際には等しくないが、等しく見せるような自然な方法がある。自然に感じられる理由として、一番に、元々はこれらがX × AからYへの双線形写像の2つの異なった表現であるからである。しかし、これはテンソル積に関するいくぶん固有な話である。圏論においての全単射の自然性は自然同型の概念が元になっている。
この用語はヒルベルト空間において、上記のhom集合の間の関係と似た関係 を満たす、随伴作用素TとUから来ている。FはGの左随伴といい、GはFの右随伴という。ただし、G自身もFとはかなり異なった右随伴を持ちうる(以下の例を見よ)。ある種の文脈においては、詳細なヒルベルト空間の随伴写像のアナロジーが可能である[1]。
これらの随伴関手の対を探し始めると、実は抽象代数では非常にありふれたことであり、他の分野でも同様であることが分かる。以下の例の節ではこの証拠を与える。さらに、普遍的構成はもっと普通にたくさんの随伴関手の対に持ち上げることができる。
を満たす、随伴作用素TとUから来ている。FはGの左随伴といい、GはFの右随伴という。ただし、G自身もFとはかなり異なった右随伴を持ちうる(以下の例を見よ)。ある種の文脈においては、詳細なヒルベルト空間の随伴写像のアナロジーが可能である[1]。
これらの随伴関手の対を探し始めると、実は抽象代数では非常にありふれたことであり、他の分野でも同様であることが分かる。以下の例の節ではこの証拠を与える。さらに、普遍的構成はもっと普通にたくさんの随伴関手の対に持ち上げることができる。
 (つまり、Aとテンソル積を取る)であり、Gは関手hom(A,–)である。ここで等号を使うのは記号の乱用である。これらの群は実際には等しくないが、等しく見せるような自然な方法がある。自然に感じられる理由として、一番に、元々はこれらがX × AからYへの双線形写像の2つの異なった表現であるからである。しかし、これはテンソル積に関するいくぶん固有な話である。圏論においての全単射の自然性は自然同型の概念が元になっている。
この用語はヒルベルト空間において、上記のhom集合の間の関係と似た関係
(つまり、Aとテンソル積を取る)であり、Gは関手hom(A,–)である。ここで等号を使うのは記号の乱用である。これらの群は実際には等しくないが、等しく見せるような自然な方法がある。自然に感じられる理由として、一番に、元々はこれらがX × AからYへの双線形写像の2つの異なった表現であるからである。しかし、これはテンソル積に関するいくぶん固有な話である。圏論においての全単射の自然性は自然同型の概念が元になっている。
この用語はヒルベルト空間において、上記のhom集合の間の関係と似た関係 を満たす、随伴作用素TとUから来ている。FはGの左随伴といい、GはFの右随伴という。ただし、G自身もFとはかなり異なった右随伴を持ちうる(以下の例を見よ)。ある種の文脈においては、詳細なヒルベルト空間の随伴写像のアナロジーが可能である[1]。
これらの随伴関手の対を探し始めると、実は抽象代数では非常にありふれたことであり、他の分野でも同様であることが分かる。以下の例の節ではこの証拠を与える。さらに、普遍的構成はもっと普通にたくさんの随伴関手の対に持ち上げることができる。
を満たす、随伴作用素TとUから来ている。FはGの左随伴といい、GはFの右随伴という。ただし、G自身もFとはかなり異なった右随伴を持ちうる(以下の例を見よ)。ある種の文脈においては、詳細なヒルベルト空間の随伴写像のアナロジーが可能である[1]。
これらの随伴関手の対を探し始めると、実は抽象代数では非常にありふれたことであり、他の分野でも同様であることが分かる。以下の例の節ではこの証拠を与える。さらに、普遍的構成はもっと普通にたくさんの随伴関手の対に持ち上げることができる。
様々な問題の定式化
[編集]
数学者は一般的には完全な随伴関手の概念を必要としているわけではない。彼らの解こうとしている問題にあっているかや証明に必要かどうかで必要な概念かどうかを判定している。圏論の初期段階である1950年代にはこれらの動機に大きく引っ張られていた。アレクサンドル・グロタンディークの時代になって、圏論は他の仕事における指針として使われるようになった。はじめは関数解析とホモロジー代数であり最終的には代数幾何で使用された。
彼が随伴関手の概念を分離したというのはおそらく誤っているといえるが、随伴の特別な役割についてグロタンディーク固有の認識はあった。例えば、彼の著名な業績のひとつに、相対型のセール双対性、くだいていうと、代数多様体の連続な族に関するセール双対性がある。この証明の全体は結局のところある関手の右随伴が存在するかということになる。これは完全に抽象的で非構成的であるが、それなりに強力でもある。
半順序集合
[編集]
すべての半順序集合は圏とみなすことができる(x ≤ yであるときに、またそのときのみ、 xとyの間には1つだけ射があるとする)。2つの半順序集合の間の随伴関手対はガロア接続と呼ばれる(そして、反変の場合は、antitoneガロア接続である)。ガロア接続の記事に多くの例がある。とくにガロア理論が一番の例である。任意のガロア接続は閉包作用素や対応する閉じた要素間の逆順序を保存する全単射に持ち上げることが出来る。
ガロア群の場合と同様に、実際の興味はしばしば双対との対応(例えば、antitone順序の同型)を詳細化していくことにある。Kaplanskyよるこのガロア理論の捕らえ方は、ここに一般的な構造があることへの認識に影響を与えた。
半順序の場合の随伴の定義は著しくつぶれているが、いくつかのテーマを与えてくれる。
●随伴は双対や同型でなくてもよいが、これらに昇格する際の候補とすることが出来る
●閉包作用素は対応するモナドによる随伴の存在を示すことがある(Kuratowski closure axiomsを参照)
●William Lawvereによる非常に一般的な解説[2] によると﹁構文と意味﹂は随伴である。つまり、Cを全ての論理(公理化)からなる集合とし、Dを全ての数学的構造からなる集合の冪集合とする。Cの各理論Tに対して、F(T)を公理Tを満たす構造全てからなる集合とし、各数学的構造の族Sに対して、G(S)はSの最小の公理化とする。このとき、F(T)がSの部分集合であることと、G(S)がTの論理的帰結であることは同値であり、﹁意味関手﹂Fは﹁構文関手﹂Gの左随伴である。
●乗算の逆としての(一般の)演算としての除算は、多くの例があるが例えば、述語論理における含意の導入規則や、環のイデアルによるイデアル商は、随伴を与えるものと見ることができる。
このような観察は全ての数学で価値のあるものである。
例
[編集]自由群
[編集]
自由群の構成は極めて普通の随伴による構成であり、上記の詳細の分かりやすくて便利な例である。
関手F : Grp ← Setは各集合YにYの要素の生成する自由群を対応させるものとし、関手G : Grp → Setは群Xにその台集合を対応させる忘却関手とする。以下に示すようにFはGの左随伴となる。
﹁終﹂普遍射。各群Xについて、群FGXはGXの生成する、すなわちXの元たちが生成する自由群である。群の準同型 をFGXの生成元を対応するXの元に写すものとする。これは自由群の普遍性から常に存在する。このとき
をFGXの生成元を対応するXの元に写すものとする。これは自由群の普遍性から常に存在する。このとき はFからXへの普遍射である。なぜなら、自由群FZからXへの群の準同型は
はFからXへの普遍射である。なぜなら、自由群FZからXへの群の準同型は を通して、一意的なZからGXへの写像経由で分解されるからである。これは(F, G)が随伴の対であることを意味する。
﹁始﹂普遍射。各集合Yに対して、GFYは単にYの生成する自由群FYの台集合である。写像
を通して、一意的なZからGXへの写像経由で分解されるからである。これは(F, G)が随伴の対であることを意味する。
﹁始﹂普遍射。各集合Yに対して、GFYは単にYの生成する自由群FYの台集合である。写像 は生成元の包含により与えられる。各
は生成元の包含により与えられる。各 はYからGへの普遍射である。なぜなら、YからGWの台集合への写像は
はYからGへの普遍射である。なぜなら、YからGWの台集合への写像は を通して、FYからWへの一意的な群の準同型経由で分解されるからである。これも(F, G)が随伴の対であることを意味する。
hom集合随伴。自由群FYから群Xへの群準同型は正確に集合Yから集合GXへの写像に対応する。すなわち、FYからXへの射は生成元への作用により完全に決定される。この対応が自然同型であることも直接確認できる。よって(F,G)に対応するhom集合の随伴が得られた。
余単位-単位随伴。εとηが自然であることは直接確かめられる。そして、余単位-単位随伴
を通して、FYからWへの一意的な群の準同型経由で分解されるからである。これも(F, G)が随伴の対であることを意味する。
hom集合随伴。自由群FYから群Xへの群準同型は正確に集合Yから集合GXへの写像に対応する。すなわち、FYからXへの射は生成元への作用により完全に決定される。この対応が自然同型であることも直接確認できる。よって(F,G)に対応するhom集合の随伴が得られた。
余単位-単位随伴。εとηが自然であることは直接確かめられる。そして、余単位-単位随伴 であることは以下のようにして示す。
1つ目の余単位-単位恒等式
であることは以下のようにして示す。
1つ目の余単位-単位恒等式  というのは各集合Yに対して、合成
というのは各集合Yに対して、合成
 が恒等射であるということである。途中の群FGFYは自由群FYの語たちから生成される自由群である。(以降、括弧でくくられた語は独立した生成元を表すことにする)。射
が恒等射であるということである。途中の群FGFYは自由群FYの語たちから生成される自由群である。(以降、括弧でくくられた語は独立した生成元を表すことにする)。射 はFYからFGFYへの群の単射準同型であり、FYの生成元yを対応するFGFYの生成元である長さ1の語 (y) に写す。射
はFYからFGFYへの群の単射準同型であり、FYの生成元yを対応するFGFYの生成元である長さ1の語 (y) に写す。射 はFGFYからFYへの群の準同型であり、生成元を対応するFYの語に写す(つまり﹁括弧を外す﹂)。これらの合成はもちろんFYの恒等射である。
2つ目の余単位-単位恒等式
はFGFYからFYへの群の準同型であり、生成元を対応するFYの語に写す(つまり﹁括弧を外す﹂)。これらの合成はもちろんFYの恒等射である。
2つ目の余単位-単位恒等式  というのは各群Xに対して、合成
というのは各群Xに対して、合成
 が恒等射であるということである。途中の集合GFGXは単にFGXの台集合である。射
が恒等射であるということである。途中の集合GFGXは単にFGXの台集合である。射 は集合GXから集合GFGXへの﹁生成元たちの包含﹂写像である。射
は集合GXから集合GFGXへの﹁生成元たちの包含﹂写像である。射 は集合GFGXから集合GXへの写像で、FGXの生成元をXの元に写す(﹁括弧を外す﹂)という群の準同型の台である。これらの合成はもちろんGXの恒等射である。
は集合GFGXから集合GXへの写像で、FGXの生成元をXの元に写す(﹁括弧を外す﹂)という群の準同型の台である。これらの合成はもちろんGXの恒等射である。
 をFGXの生成元を対応するXの元に写すものとする。これは自由群の普遍性から常に存在する。このとき
をFGXの生成元を対応するXの元に写すものとする。これは自由群の普遍性から常に存在する。このとき はFからXへの普遍射である。なぜなら、自由群FZからXへの群の準同型は
はFからXへの普遍射である。なぜなら、自由群FZからXへの群の準同型は を通して、一意的なZからGXへの写像経由で分解されるからである。これは(F, G)が随伴の対であることを意味する。
﹁始﹂普遍射。各集合Yに対して、GFYは単にYの生成する自由群FYの台集合である。写像
を通して、一意的なZからGXへの写像経由で分解されるからである。これは(F, G)が随伴の対であることを意味する。
﹁始﹂普遍射。各集合Yに対して、GFYは単にYの生成する自由群FYの台集合である。写像 は生成元の包含により与えられる。各
は生成元の包含により与えられる。各 はYからGへの普遍射である。なぜなら、YからGWの台集合への写像は
はYからGへの普遍射である。なぜなら、YからGWの台集合への写像は を通して、FYからWへの一意的な群の準同型経由で分解されるからである。これも(F, G)が随伴の対であることを意味する。
hom集合随伴。自由群FYから群Xへの群準同型は正確に集合Yから集合GXへの写像に対応する。すなわち、FYからXへの射は生成元への作用により完全に決定される。この対応が自然同型であることも直接確認できる。よって(F,G)に対応するhom集合の随伴が得られた。
余単位-単位随伴。εとηが自然であることは直接確かめられる。そして、余単位-単位随伴
を通して、FYからWへの一意的な群の準同型経由で分解されるからである。これも(F, G)が随伴の対であることを意味する。
hom集合随伴。自由群FYから群Xへの群準同型は正確に集合Yから集合GXへの写像に対応する。すなわち、FYからXへの射は生成元への作用により完全に決定される。この対応が自然同型であることも直接確認できる。よって(F,G)に対応するhom集合の随伴が得られた。
余単位-単位随伴。εとηが自然であることは直接確かめられる。そして、余単位-単位随伴 であることは以下のようにして示す。
1つ目の余単位-単位恒等式
であることは以下のようにして示す。
1つ目の余単位-単位恒等式  というのは各集合Yに対して、合成
というのは各集合Yに対して、合成
 が恒等射であるということである。途中の群FGFYは自由群FYの語たちから生成される自由群である。(以降、括弧でくくられた語は独立した生成元を表すことにする)。射
が恒等射であるということである。途中の群FGFYは自由群FYの語たちから生成される自由群である。(以降、括弧でくくられた語は独立した生成元を表すことにする)。射 はFYからFGFYへの群の単射準同型であり、FYの生成元yを対応するFGFYの生成元である長さ1の語 (y) に写す。射
はFYからFGFYへの群の単射準同型であり、FYの生成元yを対応するFGFYの生成元である長さ1の語 (y) に写す。射 はFGFYからFYへの群の準同型であり、生成元を対応するFYの語に写す(つまり﹁括弧を外す﹂)。これらの合成はもちろんFYの恒等射である。
2つ目の余単位-単位恒等式
はFGFYからFYへの群の準同型であり、生成元を対応するFYの語に写す(つまり﹁括弧を外す﹂)。これらの合成はもちろんFYの恒等射である。
2つ目の余単位-単位恒等式  というのは各群Xに対して、合成
というのは各群Xに対して、合成
 が恒等射であるということである。途中の集合GFGXは単にFGXの台集合である。射
が恒等射であるということである。途中の集合GFGXは単にFGXの台集合である。射 は集合GXから集合GFGXへの﹁生成元たちの包含﹂写像である。射
は集合GXから集合GFGXへの﹁生成元たちの包含﹂写像である。射 は集合GFGXから集合GXへの写像で、FGXの生成元をXの元に写す(﹁括弧を外す﹂)という群の準同型の台である。これらの合成はもちろんGXの恒等射である。
は集合GFGXから集合GXへの写像で、FGXの生成元をXの元に写す(﹁括弧を外す﹂)という群の準同型の台である。これらの合成はもちろんGXの恒等射である。
自由構成と忘却関手
[編集]自由対象は全て忘却関手の左随伴の例となる。ここで忘却関手は代数的対象をその台集合に写す。これらの代数的な自由関手に対しても、上記の自由群に詳細に記述したものと同様のことが一般に成り立つ。
対角関手と極限
[編集]
積、引き戻し、等化子、核はどれも圏論的な極限の例である。全ての極限関手は対応する対角関手(考えている極限の種類から決まる)の右随伴である。随伴の余単位は極限対象からの(つまり、関手圏における、考えている極限に対応する対角関手からの)定義射を与える。以下に個々の例を示す。
●積 関手Π : Grp2 → Grpを各対(X1, X2)に直積群X1×X2を対応させるものとし、関手Δ : Grp2 ← Grp を各群Xに積圏Grp2の対象(X, X)を対応させる対対角関手とする。直積群の普遍性からΠはΔの右随伴であることが分かる。この随伴のcounitは極限を定めるX1×X2からX1 と X2への2つの射影の対である射である。unitは群XからX1×X2の中への対角包含射(xを(x, x)に写す)である。
集合のデカルト積や環の直積や位相空間の直積なども同じである。さらに2つ以上の場合も素直な方法で拡張できる。もっと一般には、どの種類の極限も対角関手の右随伴である。
●核 アーベル群の準同型の圏Dを考える。Dの2つの対象f1 : A1→ B1とf2 : A2→ B2に対して、f1 から f2への射は、対(gA, gB)であって、gBf1 = f2gAを満たすもののことをいう。関手G : D→ Abを各準同型をその核に対応させるものとし、関手F : D← Abを各群Aを群準同型A → 0に対応させるものとする。GはFの右随伴であり、これは核の普遍性を示している。この随伴の余単位射は準同型の核をその始域に埋め込む射であり、単位射は群Aを準同型A → 0の核と同一視する射である。
この例の適切な変種として、線形空間や加群の核関手も右随伴である。同様に、アーベル群や線形空間や加群の余核関手が左随伴であることも分かる。
余極限と対角関手
[編集]
余積、押し出し、余等化子、余核はいずれも圏論における余極限の例えである。
全ての余極限関手は対応する対角関手(考えている余極限の種類から決まる)の左随伴である。随伴のunitは余極限対象への定義射を与える。以下に個々の例を示す。
●余積 関手F : Ab← Ab2を各アーベル群の対(X1, X2)に直和を対応させるものとし、関手G : Ab→ Ab2を各アーベル群Yに対(Y, Y)を対応させるものとする。このときFはGの左随伴である。こちらも直和の普遍性から導かれる。この随伴のunitはX1 と X2から直和への包含写像の対からなる射であり、counitは(X,X)の直和からXへの加算による射である(直和の元 (a, b)にXの元 a+b を対応させる)
同様の例として加群や線形空間の直和や、群の自由積や集合の非交和がある。
さらなる例
[編集]代数
[編集]
●非単位的環への単位元添加。これは動機の節で議論した例である。非単位的環 Rが与えられたとして、R×Zを選び、Z双線形な積を(r,0)(0,1) = (0,1)(r,0) = (r,0)、 (r,0)(s,0) = (rs,0)、 (0,1)(0,1) = (0,1)で定めることにより、乗法単位元を追加することが出来る。この構成は環の台となる非単位的環を取る関手の左随伴である。
●環の拡大。RとSを環とし、ρ : R→ Sを環の準同型とする。このときSは﹁左﹂R-加群とみなすことができ、Sとのテンソル積は関手F : R-Mod → S-Modを引き起こす。そして、Fは忘却関手G : S-Mod → R-Modの左随伴である。
●テンソル積構成。Rを環、Mを右R-加群とし、Mとのテンソル積は関手F : R-Mod → Abを引き起こす。関手G : Ab→ R-Modを、各アーベル群Aに対して、G(A) = homZ(M,A)で定めると、Fの右随伴となる。
●群環構成。整係数モノイド環構成はモノイドから環への関手を与える。この関手は各環をその台となる乗法モノイドに写す関手の左随伴である。同様に整係数群環構成は群から環への関手を与え、各環をその単元群に写す関手の左随伴である。︵整係数ではなく︶係数体 Kを与える場合、環の圏のかわりに K-代数の圏を使えば K上のモノイド環や群環が得られる。
●商体構成。整域の圏で射を単射に限ったものをDommと書くことにする。忘却関手Field → Dommは左随伴を持つ。これは全ての整域に商の体を割り当てる。
●多項式環。Ring*を基点付き可換環の圏とする(環Aとその元aの対 (A, a)を対象として、射はこの区別された元を保存する準同型とする)。忘却関手G:Ring* → Ringは左随伴を持ち、各環Rに対して(R[x], x)を割り当てる。ここでR[x]はRを係数とする多項式環である。
●アーベル化: アーベル群から群への包含関手G : Ab→ Grpを考えると、アーベル化と呼ばれる左随伴を持つ。これは各群Gに商群Gab=G/[G,G]を割り当てる。
●グロタンディーク構成: 発端は、K-理論において位相空間上のベクトル束の圏が直和の下で可換モノイド構造を持つことである。各ベクトル束︵の同値類︶に加法逆元を形式的に追加することにより、このモノイドをグロタンディーク群と呼ばれるアーベル群にすることができる。同じことだが、各群を︵逆元の存在を忘れることにより︶その台となるモノイドへ写す函手は左随伴を持つ。このようなグロタンディーク構成は、自然数からの負の整数の構成をなぞるようにすることもできるし、存在定理として使うこともある。有限項演算の代数構造の場合に対しては、そのような構成の存在性は普遍代数学やモデル理論に言及することもできるし、圏論的に適当な形での証明としても自然に述べられる。
●群の表現論におけるフロベニウス相互律によれば、表現の誘導は表現の制限の左随伴である。
位相
[編集]
●左随伴と右随伴を持つ関手。G を位相空間から集合への関手で、各位相空間にその台集合を割り当てるものとする (位相を忘れる)。G は左随伴 Fを持ち、集合 Y上に離散位相を定める。G は右随伴 Hも持ち、Y に密着位相を定める。
●懸垂とループ空間。位相空間XとYに対して、Xの懸垂 SXからYへの連続写像のホモトピー類がなす空間 [SX, Y] はXからYのループ空間ΩYへの連続写像のホモトピー類がなす空間と自然同型である。これはホモトピー論で重要である。
●ストーン–チェックコンパクト化。KHausをコンパクト[要曖昧さ回避]ハウスドルフ空間の圏とし、G : KHaus → Topを位相空間の圏への包含関手とする。このとき、Gは左随伴F : Top → KHausを持ち、ストーン–チェックコンパクト化となる。この随伴のcounitは各位相空間Xからそのストーン–チェックコンパクト化の中への連続写像である。Xがチコノフ空間であるとき、またそのときのみ、この写像は埋め込み(つまり、単射な連続開写像)である。
●層の順像と逆像。全ての連続写像f : X→ YはX上の層(集合の層、アーベル群の層、環の層など)からYの対応する層への関手f ∗を誘導し、順像関手と呼ばれる。さらに、Y上のアーベル群の層からX上のアーベル群の層への関手 f−1 も誘導され、逆像関手と呼ばれる。f −1 は f∗ の左随伴である。ここで微妙な点は連接層での左随伴は(集合の)層のそれとは異なっていることである。
●sober化。ストーン双対性の記事にあるように、位相空間の圏とsober空間の圏は随伴である。特に、この記事はpointless topologyで見つかった、sober空間とspatial localeの間の有名な双対性のための別の随伴も詳細に記述している。
圏論
[編集]
●随伴の列。関手π0を各圏にその連結成分を与える関手とすると、これは各集合に離散圏を割り当てる関手Dの左随伴である。さらに、Dは圏に対象集合を割り当てる対象関手Uの左随伴である。最後に、Uは各集合にindiscrete圏を割り当てる関手の左随伴である。
●指数対象。デカルト閉圏において–×Aで定まる自己関手C → Cは右随伴–Aを持つ。
Categorical logic
[編集]この節の加筆が望まれています。 |
- quantification Any morphism f : X → Y in a category with pullbacks induces a monotonous map acting by pullbacks (A monotonous map is a functor if we consider the preorders as categories). If this functor has a left/right adjoint, the adjoint is called and , respectively.[3]
- In the category of sets, if we choose subsets as the canonical subobjects, then these functions are given by:
- See also powerset for a slightly simplified presentation.
性質
[編集]存在性
[編集]
全ての関手 G: 𝒞 → 𝒟 が左随伴を持つわけではない。𝒞 が完備圏であるときは、左随伴を持つ関手はPeter J. Freydの随伴関手定理﹁G が左随伴を持つための必要十分条件は、それが連続(極限を保つ)かつ、ある種の﹁集合性(小ささ)﹂条件をみたすことである﹂で特徴付けられる。具体的には、𝒟 の各対象 Yに対して、集合(つまり真クラスでない集合という意味で﹁小さい﹂) Iの元で添字付けられた射の族 fi: Y→ G(Xi) が存在して、任意の射 h : Y→ G(X) が適当な元 i∈ Iと射 t: Xi→ X∈ Cを用いて h= G(t) ∘ fiと書けることが条件である。
同様のことが右随伴に関しても成り立つ。
一意性
[編集]
関手F : C← Dが2つの右随伴GとG′を持つとすると、GとG′は自然同型である。左随伴についても同様である。
逆に、FがGの左随伴であり、GとG′が自然同型であるとすると、FはG′の左随伴でもある。より一般には、︿F, G, ε, η﹀が(ε,η)をcounit-unitとする随伴であり、
σ : F→ F′
τ : G→ G′
がともに自然同型であるとすると、︿F′, G′, ε′, η′﹀も随伴である。ここで、
 であり、
であり、 は自然変換の垂直合成を表し、
は自然変換の垂直合成を表し、 は水平合成を表すとする。
は水平合成を表すとする。
 であり、
であり、 は自然変換の垂直合成を表し、
は自然変換の垂直合成を表し、 は水平合成を表すとする。
は水平合成を表すとする。
合成
[編集]
随伴は自然なやり方で合成できる。明示的に書くと、CとDとの間の随伴︿F, G, ε, η﹀とDとEとの間の随伴︿F′, G′, ε′, η′﹀が与えられたとき、関手
 は関手
は関手
 の左随伴である。さらに詳しく書くと、F′ FとG G′の間の随伴のunitとcounitは以下の合成で与えられる。
の左随伴である。さらに詳しく書くと、F′ FとG G′の間の随伴のunitとcounitは以下の合成で与えられる。
 この新しい随伴は与えられた2つの随伴の合成と呼ばれる。
これにより、小さな圏を対象とし、随伴を射とする圏を作ることが出来る。
この新しい随伴は与えられた2つの随伴の合成と呼ばれる。
これにより、小さな圏を対象とし、随伴を射とする圏を作ることが出来る。
 は関手
は関手
 の左随伴である。さらに詳しく書くと、F′ FとG G′の間の随伴のunitとcounitは以下の合成で与えられる。
の左随伴である。さらに詳しく書くと、F′ FとG G′の間の随伴のunitとcounitは以下の合成で与えられる。
 この新しい随伴は与えられた2つの随伴の合成と呼ばれる。
これにより、小さな圏を対象とし、随伴を射とする圏を作ることが出来る。
この新しい随伴は与えられた2つの随伴の合成と呼ばれる。
これにより、小さな圏を対象とし、随伴を射とする圏を作ることが出来る。
極限の保存
[編集]
随伴のもっとも重要な性質は連続性である。左随伴を持つ全ての関手(つまり右随伴である関手)は連続である(つまり圏論での極限と可換である)。右随伴を持つ全ての関手(つまり左随伴である関手)は余連続である(つまり余極限と可換である)。
数学における多くの共通の構成は極限か余極限であるので、このことはたくさんの情報をもたらす。例えば。
加法性
[編集]
CとDを前加法圏とし、F : C← Dを加法的関手とし、G : C→ DがFの右随伴であるとすると、Gも加法的関手であり、hom集合の全単射
 は、実は、アーベル群の同型である。双対的に、Gが加法的で、FがGの左随伴であるとすると、Fもまた加法的である。
さらに、CとDを加法圏(つまり、前加法圏であり有限双積をもつ)とすると、任意の随伴関手の対は自動的に加法的となる。
は、実は、アーベル群の同型である。双対的に、Gが加法的で、FがGの左随伴であるとすると、Fもまた加法的である。
さらに、CとDを加法圏(つまり、前加法圏であり有限双積をもつ)とすると、任意の随伴関手の対は自動的に加法的となる。
 は、実は、アーベル群の同型である。双対的に、Gが加法的で、FがGの左随伴であるとすると、Fもまた加法的である。
さらに、CとDを加法圏(つまり、前加法圏であり有限双積をもつ)とすると、任意の随伴関手の対は自動的に加法的となる。
は、実は、アーベル群の同型である。双対的に、Gが加法的で、FがGの左随伴であるとすると、Fもまた加法的である。
さらに、CとDを加法圏(つまり、前加法圏であり有限双積をもつ)とすると、任意の随伴関手の対は自動的に加法的となる。
関連
[編集]普遍的構成
[編集]
初めに書いたように、圏CとDの随伴は2つの普遍射の族に持ち上げることができる。片方はCの対象について、もう片方はDの対象についての普遍射である。逆に、Dの各対象から関手G : C→ Dへの普遍射が存在するとき、Gは左随伴である。
しかし、普遍的構成は随伴関手よりもっと一般的である。普遍的構成は最適化問題に似ていて、随伴の対に持ち上げられるのは、この問題が全てのDの対象について解を持つときであり、またそのときに限る(Cの対象についても同様)。
圏同値
[編集]
関手F: C→Dが圏同値の片方であるとすると、同値のもう片方の左随伴である。つまり、unitとcounitがともに同型である随伴である。
全ての随伴︿F, G, ε, η﹀はある部分圏の同値性を拡張する。Cの対象XでεXが同型射であるものからなるCの充満部分圏をC1とする。Dの対象YでηYが同型射であるものかならるDの充満部分圏をD1とする。このとき、FとGをそれぞれD1 と C1に制限した関手はこれらの部分圏の同値の反転となっている。
この意味で、随伴は一般化された逆元である。しかし、Fの右逆(つまり、関手GであってFGが1Dに自然同型なもの)は必ずしもFの右または左随伴になるとは限らない。随伴は2方向に一般化された逆である。
モナド
[編集]
全ての随伴︿F, G, ε, η﹀はDにおける関連するモナド︿T, η, μ﹀に持ち上げることができる。関手
 はT = GFで与えられる。モナドのunit
はT = GFで与えられる。モナドのunit
 は随伴のunit ηそのものである。乗法の変換
は随伴のunit ηそのものである。乗法の変換
 はμ = GεFで与えられる。双対的に、︿FG, ε, FηG﹀はCにおけるコモナドを定める。
全てのモナドが随伴から作ることができる。実際、典型的なモナドは多くの随伴から上の方法を用いて構成されている。2つの構成Eilenberg–Moore algebraとクライスリ圏はモナドから随伴を構成する問題に対する、2つの両極端の解である。
はμ = GεFで与えられる。双対的に、︿FG, ε, FηG﹀はCにおけるコモナドを定める。
全てのモナドが随伴から作ることができる。実際、典型的なモナドは多くの随伴から上の方法を用いて構成されている。2つの構成Eilenberg–Moore algebraとクライスリ圏はモナドから随伴を構成する問題に対する、2つの両極端の解である。
 はT = GFで与えられる。モナドのunit
はT = GFで与えられる。モナドのunit
 は随伴のunit ηそのものである。乗法の変換
は随伴のunit ηそのものである。乗法の変換
 はμ = GεFで与えられる。双対的に、︿FG, ε, FηG﹀はCにおけるコモナドを定める。
全てのモナドが随伴から作ることができる。実際、典型的なモナドは多くの随伴から上の方法を用いて構成されている。2つの構成Eilenberg–Moore algebraとクライスリ圏はモナドから随伴を構成する問題に対する、2つの両極端の解である。
はμ = GεFで与えられる。双対的に、︿FG, ε, FηG﹀はCにおけるコモナドを定める。
全てのモナドが随伴から作ることができる。実際、典型的なモナドは多くの随伴から上の方法を用いて構成されている。2つの構成Eilenberg–Moore algebraとクライスリ圏はモナドから随伴を構成する問題に対する、2つの両極端の解である。
脚注
[編集]- ^ arXiv.org: John C. Baez Higher-Dimensional Algebra II: 2-Hilbert Spaces.
- ^ William Lawvere, Adjointness in foundations, Dialectica, 1969, available here。今は異なる記法が使われる。Peter Smith in these lecture notes よるより簡単な紹介は、先の記事の考えにも基づいている
- ^ Saunders Mac Lane, Ieke Moerdijk, (1992) Sheaves in Geometry and Logic Springer-Verlag. ISBN 0-387-97710-4 See page 58
参考文献
[編集]- Adámek, Jiří; Herrlich, Horst; Strecker, George E. (1990) (PDF). Abstract and Concrete Categories. The joy of cats. John Wiley & Sons. ISBN 0-471-60922-6. Zbl 0695.18001
- Mac Lane, Saunders (1998). Categories for the Working Mathematician. Graduate Texts in Mathematics. 5 (2nd ed.). Springer-Verlag. ISBN 0-387-98403-8. MR1712872. Zbl 0906.18001
外部リンク
[編集]- Hazewinkel, Michiel, ed. (2001), “Adjoint functor”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
- Adjunctions Seven short lectures on adjunctions.






