テトレーション
表示
(超指数関数から転送)
テトレーション︵英: tetration︶とは、冪乗の次となる4番目のハイパー演算である。つまり、自らの冪乗を指定された回数反復する二項演算である。超冪︵ちょうべき︶ともいう。テトレーションという語はルーベン・グッドスタインによって、﹁4﹂を意味する接頭辞 tetra- と﹁繰り返し﹂を意味する iteration から作り出された[1]。
![{\displaystyle {}^{n}a:={\begin{cases}1&{\text{if }}n=0\\a^{\left[{}^{(n-1)}a\right]}&{\text{if }}n>0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e92358f7f10a6e5d945bee8fc4a413d5af320a5c) 冪乗の演算が右結合、すなわち 101010のように積みあがった指数の上側から計算していくように、テトレーションの計算も naに対する nの部分から計算していく。
定義から直ちに、次の等式が成り立つ。
冪乗の演算が右結合、すなわち 101010のように積みあがった指数の上側から計算していくように、テトレーションの計算も naに対する nの部分から計算していく。
定義から直ちに、次の等式が成り立つ。
 a と 10が互いに素であるとき、na の最後の d桁がオイラーの定理から求められる。
a と 10が互いに素であるとき、na の最後の d桁がオイラーの定理から求められる。
定義[編集]
任意の正の実数 a> 0 および非負整数 n≥ 0 に対し、次のようにテトレーション naを再帰的に定める。![{\displaystyle {}^{n}a:={\begin{cases}1&{\text{if }}n=0\\a^{\left[{}^{(n-1)}a\right]}&{\text{if }}n>0\end{cases}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e92358f7f10a6e5d945bee8fc4a413d5af320a5c) 冪乗の演算が右結合、すなわち 101010のように積みあがった指数の上側から計算していくように、テトレーションの計算も naに対する nの部分から計算していく。
定義から直ちに、次の等式が成り立つ。
冪乗の演算が右結合、すなわち 101010のように積みあがった指数の上側から計算していくように、テトレーションの計算も naに対する nの部分から計算していく。
定義から直ちに、次の等式が成り立つ。
 a と 10が互いに素であるとき、na の最後の d桁がオイラーの定理から求められる。
a と 10が互いに素であるとき、na の最後の d桁がオイラーの定理から求められる。
表記[編集]
テトレーションには多数の表記が存在する。テトレーションに使われる表記の中にはペンテーションやヘキセーションなど、より高次のハイパー演算の表記にも使用できるものもいくつかある。名称 表記 説明 ルーディ・ラッカーの表記 マウラー[2][3]とグッドスタイン[1]によって導入され、ルーディ・ラッカーの『無限と心』で広まった。 クヌースの矢印表記 矢印または添字を増やすことで拡張できる。 コンウェイのチェーン表記 数字を増やす、またはチェーンを拡張することで拡張できる。 アッカーマン関数 底が 2 のときに限り、アッカーマン関数による表記が可能。 指数関数の反復合成による表示 右辺の表記に関しては後述。 フーシュマンドの表記 フーシュマンドの論文では「ultra power」(超冪)と書かれている[4]。 ハイパー演算子表記
数字を増やすことで拡張でき、一連のハイパー演算子を与える。 ASCII表記 a^^nASCII文字で表現する際、冪乗をキャレット ^で表すことから。バウアーズの配列表記 拡張配列表記へと一般化でき、さらにBEAFおよびバードの配列表記へと一般化される[5]。
反復指数関数[編集]
反復指数関数(英: iterated exponential function)、あるいは反復冪(英: iterated exponential)とは指数関数の反復合成、あるいはその類似の関数およびその値を指して呼ばれる関数である[6][7]。以降で表記を簡単にするため、非負整数 n と正実数 a の2つのパラメータを持つ実関数 を次のように定義する:
- (n 個の a の上に x が乗っている)
この関数は他に次のような表記で書かれる。
名称 表記 説明 (指数の反復合成) 指数関数の表記 はオイラーによる。 クヌースの矢印表記 矢印の数を増やすことで拡張できる。en:Large numbersを参照。 ガリダキスの表記 底の表記が小さくならない[8]。 ASCII表記 exp_a^n(x)標準的な表記をベースにASCII文字のみを使用した表記。 J言語表記[9] x^^:(n-1)x
例[編集]
以下の表では、大部分の値が指数表記による表記すら困難なほど巨大であるため、それらの表記には底を 10 とした反復指数関数を用いた。なお小数部を持つ値はすべて近似値である。
1 1 (11) 1 (11) 1 (11) 2 4 (22) 16 (24) 65,536 (216) 3 27 (33) 7,625,597,484,987 (327) 1.258015 × 103,638,334,640,024 4 256 (44) 1.34078 ×10154 (4256) (8.1 × 10153 桁) 5 3,125 (55) 1.91101 × 102,184 (53,125) (1.3 × 102,184 桁) 6 46,656 (66) 2.65912 × 1036,305 (646,656) (2.1 × 1036,305 桁) 7 823,543 (77) 3.75982 × 10695,974 (7823,543) (3.2 × 10695,974 桁) 8 16,777,216 (88) 6.01452 × 1015,151,335 (5.4 × 1015,151,335 桁) 9 387,420,489 (99) 4.28125 × 10369,693,099 (4.1 × 10369,693,099 桁) 10 10,000,000,000 (1010) 1010,000,000,000 (1.0 × 1010,000,000,000 桁)
微積分[編集]
テトレーション naに対する aは正の実数に対して定義できるので、n を固定したときにそれぞれ微分と積分が定義できる。


区間 x ∈ (0, 1] における y = xx と y = x−x のグラフ。
1/2x、 2xの 0 から 1までの定積分は二年生の夢と呼ばれる。
 任意の正の整数 nに対し、nx の不定積分は次のようになる[11]。
任意の正の整数 nに対し、nx の不定積分は次のようになる[11]。
 ここで aj,k は
ここで aj,k は
 で与えられる有理数であり、 bj (x) は第2種不完全ガンマ関数を用いて
で与えられる有理数であり、 bj (x) は第2種不完全ガンマ関数を用いて
 で与えられる。
で与えられる。
 と収束するため、
と収束するため、
 と定義する。︵ここで、2Z、2Z+1 はそれぞれ偶数、奇数の集合を表す。︶
なお、ここで 00 が一意に決まらないにもかかわらず 20 (= 00) が定義できるのは、 abの aと bが等しいという条件下で極限を取ったからである。
と定義する。︵ここで、2Z、2Z+1 はそれぞれ偶数、奇数の集合を表す。︶
なお、ここで 00 が一意に決まらないにもかかわらず 20 (= 00) が定義できるのは、 abの aと bが等しいという条件下で極限を取ったからである。

収束または振動する点

発散する点
複素数の累乗が可能なことから、テトレーションは複素数の底に対しても定義できる。
例えばテトレーション niは対数関数の主枝を用いて定められる。このときオイラーの公式から次の式が得られる。
 従って任意の ni= a+ biに対して n+ 1i = a′ + b′i が次のように再帰的に定義できる。
従って任意の ni= a+ biに対して n+ 1i = a′ + b′i が次のように再帰的に定義できる。
 ここから以下の近似値が導かれる。
ここから以下の近似値が導かれる。
高さが定数の微分[編集]
任意の正の整数 nに対し、 nxの微分は次のようになる[10]。
高さが定数の積分[編集]

 任意の正の整数 nに対し、nx の不定積分は次のようになる[11]。
任意の正の整数 nに対し、nx の不定積分は次のようになる[11]。
 ここで aj,k は
ここで aj,k は
 で与えられる有理数であり、 bj (x) は第2種不完全ガンマ関数を用いて
で与えられる有理数であり、 bj (x) は第2種不完全ガンマ関数を用いて
 で与えられる。
で与えられる。
拡張[編集]
テトレーションは、高さが正の整数以外の場合に拡張できる。底が0[編集]
0の0乗が単純には定義できないため、 n0 は直接定義できないが、極限が と収束するため、
と収束するため、
 と定義する。︵ここで、2Z、2Z+1 はそれぞれ偶数、奇数の集合を表す。︶
なお、ここで 00 が一意に決まらないにもかかわらず 20 (= 00) が定義できるのは、 abの aと bが等しいという条件下で極限を取ったからである。
と定義する。︵ここで、2Z、2Z+1 はそれぞれ偶数、奇数の集合を表す。︶
なお、ここで 00 が一意に決まらないにもかかわらず 20 (= 00) が定義できるのは、 abの aと bが等しいという条件下で極限を取ったからである。
底が複素数[編集]


 従って任意の ni= a+ biに対して n+ 1i = a′ + b′i が次のように再帰的に定義できる。
従って任意の ni= a+ biに対して n+ 1i = a′ + b′i が次のように再帰的に定義できる。
 ここから以下の近似値が導かれる。
ここから以下の近似値が導かれる。
近似値 [注 1]
同様に値を逆向きに求めていくことで 0i = 1、 −1i = 0 が得られる。 niの値を複素平面上にプロットすると、点列は渦巻状に極限値 0.4383 + 0.3606i へと近づく。この値は n→∞ のときと解釈できる。
このようなテトレーションの列に関する研究はオイラーの時代から続けられてきているものの、そのカオス的な振る舞いのために不明な所が多い。これまでに発表された研究のほとんどは、無限反復指数関数の収束について焦点を当てたものである。現在の研究は高性能のコンピュータを用いたフラクタルと数式処理システムの出現に大きな恩恵を受けている。テトレーションについて分かっていることの多くは、複素力学系の一般的な知識と、指数写像の専門的な研究によるものである。

 における
における  のグラフ
のグラフ
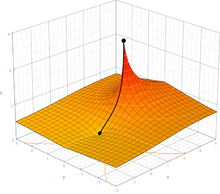
関数  の複素平面上のグラフ。実数値無限反復指数関数を黒い曲線で示した。
ある範囲の底 aに対して limn→∞ na は有限の値に収束するので、この範囲においてテトレーションは高さ無限大の場合へ拡張できる。例えば limn→∞ n(√2) は収束して、その値は 2であるから、 ∞(√2) = 2 であると言える。
一般に無限反復指数関数
の複素平面上のグラフ。実数値無限反復指数関数を黒い曲線で示した。
ある範囲の底 aに対して limn→∞ na は有限の値に収束するので、この範囲においてテトレーションは高さ無限大の場合へ拡張できる。例えば limn→∞ n(√2) は収束して、その値は 2であるから、 ∞(√2) = 2 であると言える。
一般に無限反復指数関数  は、 nが無限大に向かうときの nxの極限として定義される。これが e−e ≤ x≤ e1/e ︵およそ 0.066 から 1.44︶の範囲で収束することはオイラーによって示された[12]。
極限値 ∞x が存在するとき、これは方程式
は、 nが無限大に向かうときの nxの極限として定義される。これが e−e ≤ x≤ e1/e ︵およそ 0.066 から 1.44︶の範囲で収束することはオイラーによって示された[12]。
極限値 ∞x が存在するとき、これは方程式
高さが無限大[編集]

 における
における  のグラフ
のグラフ

 の複素平面上のグラフ。実数値無限反復指数関数を黒い曲線で示した。
ある範囲の底 aに対して limn→∞ na は有限の値に収束するので、この範囲においてテトレーションは高さ無限大の場合へ拡張できる。例えば limn→∞ n(√2) は収束して、その値は 2であるから、 ∞(√2) = 2 であると言える。
一般に無限反復指数関数
の複素平面上のグラフ。実数値無限反復指数関数を黒い曲線で示した。
ある範囲の底 aに対して limn→∞ na は有限の値に収束するので、この範囲においてテトレーションは高さ無限大の場合へ拡張できる。例えば limn→∞ n(√2) は収束して、その値は 2であるから、 ∞(√2) = 2 であると言える。
一般に無限反復指数関数  は、 nが無限大に向かうときの nxの極限として定義される。これが e−e ≤ x≤ e1/e ︵およそ 0.066 から 1.44︶の範囲で収束することはオイラーによって示された[12]。
極限値 ∞x が存在するとき、これは方程式
は、 nが無限大に向かうときの nxの極限として定義される。これが e−e ≤ x≤ e1/e ︵およそ 0.066 から 1.44︶の範囲で収束することはオイラーによって示された[12]。
極限値 ∞x が存在するとき、これは方程式
(1)
を満たす正の実数に等しい。
式(1)より x= (∞x)1/∞x であり、このとき右辺の最大値が e1/e であることから、 x> e1/e については極限値が存在しないことがわかる。また  は
は  の逆関数︵の分岐の下部︶であることがわかる。
式(1)から、極限値 ∞z をランベルトのW関数 Wを用いて次のように定義することで複素数の底 zに対しても拡張される。
の逆関数︵の分岐の下部︶であることがわかる。
式(1)から、極限値 ∞z をランベルトのW関数 Wを用いて次のように定義することで複素数の底 zに対しても拡張される。
 は
は  の逆関数︵の分岐の下部︶であることがわかる。
式(1)から、極限値 ∞z をランベルトのW関数 Wを用いて次のように定義することで複素数の底 zに対しても拡張される。
の逆関数︵の分岐の下部︶であることがわかる。
式(1)から、極限値 ∞z をランベルトのW関数 Wを用いて次のように定義することで複素数の底 zに対しても拡張される。
(2)
高さが非正[編集]
定義より
 が成り立つので、この関係を k≤ 0 に対しても帰納的に拡張し
が成り立つので、この関係を k≤ 0 に対しても帰納的に拡張し
 と定義する。
ただし、定義できるのは n= −1 までで、log 0 が存在しないため n= −2 に対しては定義できず、従って n≤ −2 に対して拡張できない。
と定義する。
ただし、定義できるのは n= −1 までで、log 0 が存在しないため n= −2 に対しては定義できず、従って n≤ −2 に対して拡張できない。
 が成立する。
三つ目の条件は著者およびアプローチによって異なる。実数高さへの拡張には二つの主要なアプローチが存在し、一つは正則性、もう一つは微分可能性に基づいたものである。これらの二つのアプローチは、相反する結果を導くことから互いに大きく異なるとされ、調和は難しいと考えられている。
長さ 1の区間で xaが定義されれば、任意の x>−2 に対し容易に拡張される。
が成立する。
三つ目の条件は著者およびアプローチによって異なる。実数高さへの拡張には二つの主要なアプローチが存在し、一つは正則性、もう一つは微分可能性に基づいたものである。これらの二つのアプローチは、相反する結果を導くことから互いに大きく異なるとされ、調和は難しいと考えられている。
長さ 1の区間で xaが定義されれば、任意の x>−2 に対し容易に拡張される。

xa の一次近似によるグラフ︵a = 4, e, 2, 1.5, 0.5︶。漸近線はx = -2
一次近似︵連続性のもと微分可能性を近似︶は次のように与えられる。
 ゆえに
ゆえに
 が成り立つので、この関係を k≤ 0 に対しても帰納的に拡張し
が成り立つので、この関係を k≤ 0 に対しても帰納的に拡張し
 と定義する。
ただし、定義できるのは n= −1 までで、log 0 が存在しないため n= −2 に対しては定義できず、従って n≤ −2 に対して拡張できない。
と定義する。
ただし、定義できるのは n= −1 までで、log 0 が存在しないため n= −2 に対しては定義できず、従って n≤ −2 に対して拡張できない。
高さが実数[編集]
テトレーションを高さ実数または複素数へ拡張する、という一般的な問題への広く受け入れられた解答は今のところ存在しない。いくつかのアプローチについて以下で述べる。 一般にこの問題は任意の実数 a> 0 に対し、実数 x> −2 で定義され、次の条件を満たす超指数関数 f (x) = xaを求めるものである。 ●f (0) = 1、 f (−1) = 0 ●任意の実数 x> −1 に対し f (x) = a↑↑(f (x−1)) ●三つ目の条件は通常次の中のどれかである。 ●連続性︵通常は x> 0 における a、 xについての連続性︶ ●微分可能性︵x についての 1、 2、 k回または無限回微分可能性︶ ●正則性︵x についての 2階微分可能性を含む︶ 任意の実数 x> 0 に対して が成立する。
三つ目の条件は著者およびアプローチによって異なる。実数高さへの拡張には二つの主要なアプローチが存在し、一つは正則性、もう一つは微分可能性に基づいたものである。これらの二つのアプローチは、相反する結果を導くことから互いに大きく異なるとされ、調和は難しいと考えられている。
長さ 1の区間で xaが定義されれば、任意の x>−2 に対し容易に拡張される。
が成立する。
三つ目の条件は著者およびアプローチによって異なる。実数高さへの拡張には二つの主要なアプローチが存在し、一つは正則性、もう一つは微分可能性に基づいたものである。これらの二つのアプローチは、相反する結果を導くことから互いに大きく異なるとされ、調和は難しいと考えられている。
長さ 1の区間で xaが定義されれば、任意の x>−2 に対し容易に拡張される。
一次近似[編集]

 ゆえに
ゆえに
近似 定義域
と以下続く。但しこの微分可能性はあくまで区分的なものである。整数 xを境に微分係数が lna倍されるため、︵a = eの場合を除いて︶整数 xにおいて微分不可能となる。
以下は値の計算例である。


Ultra exponential function[編集]
フーシュマンドは ultra exponential function という関数を導入した[13]。 これはテトレーションの一次近似を表し、 uxpa (x) と表記される。 uxpa は、次の定理によって一意に定められる。
定理 ―
 に対し、連続な関数
に対し、連続な関数  が条件
●任意の実数
が条件
●任意の実数  に対し
に対し  ●
● ●
● は
は  で微分可能
●
で微分可能
● は
は  で広義単調増加か広義単調減少
●
で広義単調増加か広義単調減少
● を満たすとき、
を満たすとき、 は次の方程式によって一意に定まる。
は次の方程式によって一意に定まる。
![{\displaystyle f(x)=\exp _{a}^{[x]}\left(a^{\lbrace {x}\rbrace }\right)=\exp _{a}^{[x+1]}\left(\lbrace {x}\rbrace \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e1c3d15069338e81667ec566e62a035c6f9a387) 但し
但し ![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d) はガウス記号であり、また
はガウス記号であり、また ![{\displaystyle \lbrace {x}\rbrace =x-[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/967e8641a2a695a5a46c3089b4337d3b10fc0d2f) である。
である。
 に対し、連続な関数
に対し、連続な関数  が条件
●任意の実数
が条件
●任意の実数  に対し
に対し  ●
● ●
● は
は  で微分可能
●
で微分可能
● は
は  で広義単調増加か広義単調減少
●
で広義単調増加か広義単調減少
● を満たすとき、
を満たすとき、 は次の方程式によって一意に定まる。
は次の方程式によって一意に定まる。
![{\displaystyle f(x)=\exp _{a}^{[x]}\left(a^{\lbrace {x}\rbrace }\right)=\exp _{a}^{[x+1]}\left(\lbrace {x}\rbrace \right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4e1c3d15069338e81667ec566e62a035c6f9a387) 但し
但し ![{\displaystyle [x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/07548563c21e128890501e14eb7c80ee2d6fda4d) はガウス記号であり、また
はガウス記号であり、また ![{\displaystyle \lbrace {x}\rbrace =x-[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/967e8641a2a695a5a46c3089b4337d3b10fc0d2f) である。
である。
証明は、三番目から五番目の条件より f が [−1, 0] で線型となることから従う。
フーシュマンドはさらに次のような一意性定理を導いた。
定理 ― 連続な関数 が条件
- 任意の に対し
- は で下に凸
を満たすとき、 は に等しい。
証明は先とほぼ同様である。漸化式より  となること、三番目の条件より fが (−1, 0) で線型となることから従う。
定理より、 x>−1 に対し f (x) = exp (f (x−1)) および f (0) = 1 であって、かつ (−1, +∞) で下に凸であるような関数 fは唯一 uxp のみである。f が十分微分可能であるためには (−1, 0) で極値を持つ必要がある。
となること、三番目の条件より fが (−1, 0) で線型となることから従う。
定理より、 x>−1 に対し f (x) = exp (f (x−1)) および f (0) = 1 であって、かつ (−1, +∞) で下に凸であるような関数 fは唯一 uxp のみである。f が十分微分可能であるためには (−1, 0) で極値を持つ必要がある。

xa の二次近似によるグラフ︵a = 4, e, 2, 1.5, 0.5︶
︵微分可能性についての︶二次近似は次のように与えられる。
 これは任意の x> 0 について微分可能であるが二階微分可能でない。a = eのときこれは一次近似に等しくなる。
三次近似および高次への一般化は次のように与えられる[14]。
これは任意の x> 0 について微分可能であるが二階微分可能でない。a = eのときこれは一次近似に等しくなる。
三次近似および高次への一般化は次のように与えられる[14]。

複素平面上にテトレーション  を解析接続したものを描画。
を解析接続したものを描画。  と
と を太い曲線で示した。
次の条件を満たす関数 Fが一意に定まる事が証明されている[15] 。
●F (z + 1) = exp (F (x))
●F (0) = 1
●z→±i∞ のとき F (z) が対数関数の不動点︵およそ 0.318 ± 1.337i ︶に近づく
●実数 z< −2 を除く複素平面全域で正則
この関数 Fを右図に示す。また、底が eではない場合についても、底が
を太い曲線で示した。
次の条件を満たす関数 Fが一意に定まる事が証明されている[15] 。
●F (z + 1) = exp (F (x))
●F (0) = 1
●z→±i∞ のとき F (z) が対数関数の不動点︵およそ 0.318 ± 1.337i ︶に近づく
●実数 z< −2 を除く複素平面全域で正則
この関数 Fを右図に示す。また、底が eではない場合についても、底が よりも大きい場合については同様に証明されている。倍精度浮動小数点数近似はオンラインで公開されている[16]。
よりも大きい場合については同様に証明されている。倍精度浮動小数点数近似はオンラインで公開されている[16]。
 ここで αn、 βn は十分速く減衰する実数列であり、少なくとも実軸の近くで A (z)、 B (z) を収束させるとする。
この関数 Sは Fと同様に最初の二つの条件 S (z + 1) = exp (S (z))、 S (0) = 1 を満たす。また αn、 βn が十分速く 0 に近づくとき、S は正の実軸近傍で解析的となる。しかし αn、 βn が全て 0 でない場合、S は新たに大量の特異点と不連続線を複素平面上に持つことになる。これは sin (z)、 cos (z) が虚軸に沿って指数関数的に増大するためである。これらの特異点は αn、 βn が小さければ小さいほど実軸から離れていくため、 Sが正則であるためには全ての αn、 βn が 0となる、即ち S= Fであればよい。
実解析上のテトレーションは一意的に定まらないので、複素平面への拡張は一意性に必要である。
ここで αn、 βn は十分速く減衰する実数列であり、少なくとも実軸の近くで A (z)、 B (z) を収束させるとする。
この関数 Sは Fと同様に最初の二つの条件 S (z + 1) = exp (S (z))、 S (0) = 1 を満たす。また αn、 βn が十分速く 0 に近づくとき、S は正の実軸近傍で解析的となる。しかし αn、 βn が全て 0 でない場合、S は新たに大量の特異点と不連続線を複素平面上に持つことになる。これは sin (z)、 cos (z) が虚軸に沿って指数関数的に増大するためである。これらの特異点は αn、 βn が小さければ小さいほど実軸から離れていくため、 Sが正則であるためには全ての αn、 βn が 0となる、即ち S= Fであればよい。
実解析上のテトレーションは一意的に定まらないので、複素平面への拡張は一意性に必要である。
 と
と に対し、
に対し、 は整数か。[17] 特に 4x= 2 の正の解 xは有理数か[要出典]。
は整数か。[17] 特に 4x= 2 の正の解 xは有理数か[要出典]。

y = √xs のグラフ。
超平方根︵英: super square root︶は 2xの逆であり、二つの等価な表記 ssrt(x), √xs を持つ。
この関数は次のようなランベルトのW関数による表示を持つ。[18]
 またこの関数により、冪根と対数の間の鏡映的な関係が表れる。次の方程式は y= ssrt xのときに真となる。
またこの関数により、冪根と対数の間の鏡映的な関係が表れる。次の方程式は y= ssrt xのときに真となる。
![{\displaystyle {\sqrt[{y}]{x}}=\log _{y}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d71585c84cda67f69928d975bd8d1f012355543) 平方根と同様に超平方根は一つとは限らない。ただし、平方根と異なり超平方根の個数を決定するのは容易とは言えない。一般に、e−1/e < x<1 のとき xは二つの正の超平方根を 0 と1の間に持ち、1 < xのとき xは1より大きい一つの正の超平方根を持ち、0 < x< e−1/e のとき xは超平方根を実数の範囲で持たない。しかし上の式より、任意の x(≠ 1) は可算無限個の超平方根を複素数の範囲で持つことが従う。[18]
超平方根はネットワークのクラスタサイズを決定するのに使用される。[19]
平方根と同様に超平方根は一つとは限らない。ただし、平方根と異なり超平方根の個数を決定するのは容易とは言えない。一般に、e−1/e < x<1 のとき xは二つの正の超平方根を 0 と1の間に持ち、1 < xのとき xは1より大きい一つの正の超平方根を持ち、0 < x< e−1/e のとき xは超平方根を実数の範囲で持たない。しかし上の式より、任意の x(≠ 1) は可算無限個の超平方根を複素数の範囲で持つことが従う。[18]
超平方根はネットワークのクラスタサイズを決定するのに使用される。[19]

 という風に拡張できる。そしてテトレーションの回数を数え上げるペンテーションを定義することができ、
という風に拡張できる。そしてテトレーションの回数を数え上げるペンテーションを定義することができ、 と表せる。
同じようにヘキセーションも定義できる(
と表せる。
同じようにヘキセーションも定義できる( )。この拡張を一般化してクヌースの矢印表記ができる。
またテトレーションはハイパーE表記で
)。この拡張を一般化してクヌースの矢印表記ができる。
またテトレーションはハイパーE表記で と書ける。
と書ける。
 となること、三番目の条件より fが (−1, 0) で線型となることから従う。
定理より、 x>−1 に対し f (x) = exp (f (x−1)) および f (0) = 1 であって、かつ (−1, +∞) で下に凸であるような関数 fは唯一 uxp のみである。f が十分微分可能であるためには (−1, 0) で極値を持つ必要がある。
となること、三番目の条件より fが (−1, 0) で線型となることから従う。
定理より、 x>−1 に対し f (x) = exp (f (x−1)) および f (0) = 1 であって、かつ (−1, +∞) で下に凸であるような関数 fは唯一 uxp のみである。f が十分微分可能であるためには (−1, 0) で極値を持つ必要がある。
より高次の近似[編集]

 これは任意の x> 0 について微分可能であるが二階微分可能でない。a = eのときこれは一次近似に等しくなる。
三次近似および高次への一般化は次のように与えられる[14]。
これは任意の x> 0 について微分可能であるが二階微分可能でない。a = eのときこれは一次近似に等しくなる。
三次近似および高次への一般化は次のように与えられる[14]。
高さが複素数[編集]

 を解析接続したものを描画。
を解析接続したものを描画。  と
と を太い曲線で示した。
次の条件を満たす関数 Fが一意に定まる事が証明されている[15] 。
●F (z + 1) = exp (F (x))
●F (0) = 1
●z→±i∞ のとき F (z) が対数関数の不動点︵およそ 0.318 ± 1.337i ︶に近づく
●実数 z< −2 を除く複素平面全域で正則
この関数 Fを右図に示す。また、底が eではない場合についても、底が
を太い曲線で示した。
次の条件を満たす関数 Fが一意に定まる事が証明されている[15] 。
●F (z + 1) = exp (F (x))
●F (0) = 1
●z→±i∞ のとき F (z) が対数関数の不動点︵およそ 0.318 ± 1.337i ︶に近づく
●実数 z< −2 を除く複素平面全域で正則
この関数 Fを右図に示す。また、底が eではない場合についても、底が よりも大きい場合については同様に証明されている。倍精度浮動小数点数近似はオンラインで公開されている[16]。
よりも大きい場合については同様に証明されている。倍精度浮動小数点数近似はオンラインで公開されている[16]。
一意性[編集]
テトレーションを一意に定めるためには正則性の条件が重要となる。いま、関数 Fに対し関数 Sを次のように構成する。 ここで αn、 βn は十分速く減衰する実数列であり、少なくとも実軸の近くで A (z)、 B (z) を収束させるとする。
この関数 Sは Fと同様に最初の二つの条件 S (z + 1) = exp (S (z))、 S (0) = 1 を満たす。また αn、 βn が十分速く 0 に近づくとき、S は正の実軸近傍で解析的となる。しかし αn、 βn が全て 0 でない場合、S は新たに大量の特異点と不連続線を複素平面上に持つことになる。これは sin (z)、 cos (z) が虚軸に沿って指数関数的に増大するためである。これらの特異点は αn、 βn が小さければ小さいほど実軸から離れていくため、 Sが正則であるためには全ての αn、 βn が 0となる、即ち S= Fであればよい。
実解析上のテトレーションは一意的に定まらないので、複素平面への拡張は一意性に必要である。
ここで αn、 βn は十分速く減衰する実数列であり、少なくとも実軸の近くで A (z)、 B (z) を収束させるとする。
この関数 Sは Fと同様に最初の二つの条件 S (z + 1) = exp (S (z))、 S (0) = 1 を満たす。また αn、 βn が十分速く 0 に近づくとき、S は正の実軸近傍で解析的となる。しかし αn、 βn が全て 0 でない場合、S は新たに大量の特異点と不連続線を複素平面上に持つことになる。これは sin (z)、 cos (z) が虚軸に沿って指数関数的に増大するためである。これらの特異点は αn、 βn が小さければ小さいほど実軸から離れていくため、 Sが正則であるためには全ての αn、 βn が 0となる、即ち S= Fであればよい。
実解析上のテトレーションは一意的に定まらないので、複素平面への拡張は一意性に必要である。
未解決問題[編集]
●nπ, neが整数になるような正の整数 nは存在するか。特に 4π(≈9.080222455390617769723931713×10666262452970848503) は整数か[要出典]。 ●与えられた自然数 と
と に対し、
に対し、 は整数か。[17] 特に 4x= 2 の正の解 xは有理数か[要出典]。
は整数か。[17] 特に 4x= 2 の正の解 xは有理数か[要出典]。
逆関係[編集]
冪は冪根と対数の二つの逆関係を持つ。これに倣って、以下テトレーションの逆関係をそれぞれ超冪根︵英: super-root︶と超対数︵英語: super-logarithm︶と呼ぶ。超冪根[編集]
超冪根はテトレーションの底に関する逆関係である。超平方根[編集]

 またこの関数により、冪根と対数の間の鏡映的な関係が表れる。次の方程式は y= ssrt xのときに真となる。
またこの関数により、冪根と対数の間の鏡映的な関係が表れる。次の方程式は y= ssrt xのときに真となる。
![{\displaystyle {\sqrt[{y}]{x}}=\log _{y}x}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1d71585c84cda67f69928d975bd8d1f012355543) 平方根と同様に超平方根は一つとは限らない。ただし、平方根と異なり超平方根の個数を決定するのは容易とは言えない。一般に、e−1/e < x<1 のとき xは二つの正の超平方根を 0 と1の間に持ち、1 < xのとき xは1より大きい一つの正の超平方根を持ち、0 < x< e−1/e のとき xは超平方根を実数の範囲で持たない。しかし上の式より、任意の x(≠ 1) は可算無限個の超平方根を複素数の範囲で持つことが従う。[18]
超平方根はネットワークのクラスタサイズを決定するのに使用される。[19]
平方根と同様に超平方根は一つとは限らない。ただし、平方根と異なり超平方根の個数を決定するのは容易とは言えない。一般に、e−1/e < x<1 のとき xは二つの正の超平方根を 0 と1の間に持ち、1 < xのとき xは1より大きい一つの正の超平方根を持ち、0 < x< e−1/e のとき xは超平方根を実数の範囲で持たない。しかし上の式より、任意の x(≠ 1) は可算無限個の超平方根を複素数の範囲で持つことが従う。[18]
超平方根はネットワークのクラスタサイズを決定するのに使用される。[19]
その他の超冪根[編集]
任意の整数 n>2 に対して nxは定義され、x ≥ 1 のとき増加となり n1 = 1 を満たす。従って x≥ 1 のとき n√xs は存在する。しかし上述した一次近似を用いた場合、−1 < y≤ 0 のとき yxは xによらず y+ 1 となり、従ってこの場合 x= y√y + 1s は存在しない。 超平方根のほか n次の超冪根も同様の記号を用いて n√xs と表すことができる。 超冪根は高さが無限大の場合へと拡張することができ、これは 1/e ≤ x≤ eの場合に限り問題なく定義される︵#高さが無限大を参照︶。∞x が存在するとき ∞x = x∞x が成り立つことから、無限次の超冪根は初等関数によって ∞√xs = x1/x と表すことができる。例えば ∞√2s = 21/2 = √2 となる。 n を任意の正の整数とするとゲルフォント=シュナイダーの定理より、超平方根 √ns は整数または超越数となり、超立方根 3√ns は整数または無理数︵これが超越数かどうかは知られていない︶となる。超対数[編集]
超対数はテトレーションの高さに関する逆関係である。 テトレーション xaを xに関して連続的に増加するものとして定義すると、任意の実数 xに対し超対数 sloga x(a >1) が定義される。 この関数 sloga xは以下の式を満たす。
さらなる拡張[編集]
テトレーションは という風に拡張できる。そしてテトレーションの回数を数え上げるペンテーションを定義することができ、
という風に拡張できる。そしてテトレーションの回数を数え上げるペンテーションを定義することができ、 と表せる。
同じようにヘキセーションも定義できる(
と表せる。
同じようにヘキセーションも定義できる( )。この拡張を一般化してクヌースの矢印表記ができる。
またテトレーションはハイパーE表記で
)。この拡張を一般化してクヌースの矢印表記ができる。
またテトレーションはハイパーE表記で と書ける。
と書ける。
脚注[編集]
注記[編集]
出典[編集]
(一)^ abGoodstein, R. L. (1947). “Transfinite Ordinals in Recursive Number Theory”. The Journal of Symbolic Logic 12 (4): 123–129. doi:10.2307/2266486. ISSN 0022-4812.
(二)^ Maurer, Hans (1901). “Über die Funktion ![{\displaystyle y=x^{[x^{[x(\cdots )]}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab69cf15b7afca0a5f9cc89da314bbb89b61a749) für ganzzahliges Argument (Abundanzen)”. Mittheilungen der Mathematische Gesellschaft in Hamburg 4: 33–50.
(三)^ Knoebel, R. Arthur (1981). “Exponentials Reiterated”. The American Mathematical Monthly 88 (4): 235–252. doi:10.2307/2320546. ISSN 0002-9890.
(四)^ Hooshmand, M. H. (2006-08-01). “Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8): 549–558. doi:10.1080/10652460500422247. ISSN 1065-2469.
(五)^ “Exploding Array Function”. Jonathan Bowers. 2021年7月30日閲覧。
(六)^ Daniel B. Shapiro and S. David Shapiro (2007). “Iterated Exponents in Number Theory” (pdf). Electronic Journal of Combinatorial Number Theory 7 (A23) 2021年7月30日閲覧。.
(七)^ Jekusiel Ginsburg (1945). “Iterated Exponentials” (pdf). Scripa Mathematica 11: 340–353 2021年7月30日閲覧。.
(八)^ Ioannis Galidakis. On Extending hyper4 and Knuth’s Up-arrow Notation to the Reals[リンク切れ]
(九)^ “Power Verb”. J Vocabulary. J Software. 2011年10月28日閲覧。
(十)^ Edward Drake Roe, Jr. (1898). “68”. The American Mathematical Monthly 5: 110. doi:10.2307/2971013.
(11)^ I. N. Galidakis, (2004). “On an Application of Lambert’s W Function to Infinite Exponentials”. Complex Variables Th. Appl. 49: 759–780. doi:10.1080/02781070412331298796. ISSN 0278-1077.
(12)^ Euler, L., "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2, 29–51, 1783. Reprinted in Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig, Germany: Teubner, pp. 350–369, 1921. (facsimile)
(13)^ M. H. Hooshmand, (2006). “Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8): 549–558. doi:10.1080/10652460500422247.
(14)^ Andrew Robbins. Solving for the Analytic Piecewise Extension of Tetration and the Super-logarithm
(15)^ W. Paulsen and S. Cowgill (March 2017). “Solving
für ganzzahliges Argument (Abundanzen)”. Mittheilungen der Mathematische Gesellschaft in Hamburg 4: 33–50.
(三)^ Knoebel, R. Arthur (1981). “Exponentials Reiterated”. The American Mathematical Monthly 88 (4): 235–252. doi:10.2307/2320546. ISSN 0002-9890.
(四)^ Hooshmand, M. H. (2006-08-01). “Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8): 549–558. doi:10.1080/10652460500422247. ISSN 1065-2469.
(五)^ “Exploding Array Function”. Jonathan Bowers. 2021年7月30日閲覧。
(六)^ Daniel B. Shapiro and S. David Shapiro (2007). “Iterated Exponents in Number Theory” (pdf). Electronic Journal of Combinatorial Number Theory 7 (A23) 2021年7月30日閲覧。.
(七)^ Jekusiel Ginsburg (1945). “Iterated Exponentials” (pdf). Scripa Mathematica 11: 340–353 2021年7月30日閲覧。.
(八)^ Ioannis Galidakis. On Extending hyper4 and Knuth’s Up-arrow Notation to the Reals[リンク切れ]
(九)^ “Power Verb”. J Vocabulary. J Software. 2011年10月28日閲覧。
(十)^ Edward Drake Roe, Jr. (1898). “68”. The American Mathematical Monthly 5: 110. doi:10.2307/2971013.
(11)^ I. N. Galidakis, (2004). “On an Application of Lambert’s W Function to Infinite Exponentials”. Complex Variables Th. Appl. 49: 759–780. doi:10.1080/02781070412331298796. ISSN 0278-1077.
(12)^ Euler, L., "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2, 29–51, 1783. Reprinted in Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig, Germany: Teubner, pp. 350–369, 1921. (facsimile)
(13)^ M. H. Hooshmand, (2006). “Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8): 549–558. doi:10.1080/10652460500422247.
(14)^ Andrew Robbins. Solving for the Analytic Piecewise Extension of Tetration and the Super-logarithm
(15)^ W. Paulsen and S. Cowgill (March 2017). “Solving  in the complex plane”. Advances in Computational Mathematics: 1-22. doi:10.1007/s10444-017-9524-1.
(16)^ テトレーションおよびその導関数を計算・描画するMathematicaコード
(17)^ Marshall, Ash J., and Tan, Yiren, "A rational number of the form aawith airrational", Mathematical Gazette 96, March 2012, pp. 106-109.
(18)^ ab
Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J.; Knuth, D. E. (1996). “On the Lambert W function” (PostScript). Advances in Computational Mathematics 5: 333. doi:10.1007/BF02124750.
(19)^ BOSTON UNIVERSITY COLLEGE OF ENGINEERING – EFFICIENT SELF-ORGANIZATION OF LARGE WIRELESS SENSOR NETWORKS
in the complex plane”. Advances in Computational Mathematics: 1-22. doi:10.1007/s10444-017-9524-1.
(16)^ テトレーションおよびその導関数を計算・描画するMathematicaコード
(17)^ Marshall, Ash J., and Tan, Yiren, "A rational number of the form aawith airrational", Mathematical Gazette 96, March 2012, pp. 106-109.
(18)^ ab
Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J.; Knuth, D. E. (1996). “On the Lambert W function” (PostScript). Advances in Computational Mathematics 5: 333. doi:10.1007/BF02124750.
(19)^ BOSTON UNIVERSITY COLLEGE OF ENGINEERING – EFFICIENT SELF-ORGANIZATION OF LARGE WIRELESS SENSOR NETWORKS
![{\displaystyle y=x^{[x^{[x(\cdots )]}]}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ab69cf15b7afca0a5f9cc89da314bbb89b61a749) für ganzzahliges Argument (Abundanzen)”. Mittheilungen der Mathematische Gesellschaft in Hamburg 4: 33–50.
(三)^ Knoebel, R. Arthur (1981). “Exponentials Reiterated”. The American Mathematical Monthly 88 (4): 235–252. doi:10.2307/2320546. ISSN 0002-9890.
(四)^ Hooshmand, M. H. (2006-08-01). “Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8): 549–558. doi:10.1080/10652460500422247. ISSN 1065-2469.
(五)^ “Exploding Array Function”. Jonathan Bowers. 2021年7月30日閲覧。
(六)^ Daniel B. Shapiro and S. David Shapiro (2007). “Iterated Exponents in Number Theory” (pdf). Electronic Journal of Combinatorial Number Theory 7 (A23) 2021年7月30日閲覧。.
(七)^ Jekusiel Ginsburg (1945). “Iterated Exponentials” (pdf). Scripa Mathematica 11: 340–353 2021年7月30日閲覧。.
(八)^ Ioannis Galidakis. On Extending hyper4 and Knuth’s Up-arrow Notation to the Reals[リンク切れ]
(九)^ “Power Verb”. J Vocabulary. J Software. 2011年10月28日閲覧。
(十)^ Edward Drake Roe, Jr. (1898). “68”. The American Mathematical Monthly 5: 110. doi:10.2307/2971013.
(11)^ I. N. Galidakis, (2004). “On an Application of Lambert’s W Function to Infinite Exponentials”. Complex Variables Th. Appl. 49: 759–780. doi:10.1080/02781070412331298796. ISSN 0278-1077.
(12)^ Euler, L., "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2, 29–51, 1783. Reprinted in Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig, Germany: Teubner, pp. 350–369, 1921. (facsimile)
(13)^ M. H. Hooshmand, (2006). “Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8): 549–558. doi:10.1080/10652460500422247.
(14)^ Andrew Robbins. Solving for the Analytic Piecewise Extension of Tetration and the Super-logarithm
(15)^ W. Paulsen and S. Cowgill (March 2017). “Solving
für ganzzahliges Argument (Abundanzen)”. Mittheilungen der Mathematische Gesellschaft in Hamburg 4: 33–50.
(三)^ Knoebel, R. Arthur (1981). “Exponentials Reiterated”. The American Mathematical Monthly 88 (4): 235–252. doi:10.2307/2320546. ISSN 0002-9890.
(四)^ Hooshmand, M. H. (2006-08-01). “Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8): 549–558. doi:10.1080/10652460500422247. ISSN 1065-2469.
(五)^ “Exploding Array Function”. Jonathan Bowers. 2021年7月30日閲覧。
(六)^ Daniel B. Shapiro and S. David Shapiro (2007). “Iterated Exponents in Number Theory” (pdf). Electronic Journal of Combinatorial Number Theory 7 (A23) 2021年7月30日閲覧。.
(七)^ Jekusiel Ginsburg (1945). “Iterated Exponentials” (pdf). Scripa Mathematica 11: 340–353 2021年7月30日閲覧。.
(八)^ Ioannis Galidakis. On Extending hyper4 and Knuth’s Up-arrow Notation to the Reals[リンク切れ]
(九)^ “Power Verb”. J Vocabulary. J Software. 2011年10月28日閲覧。
(十)^ Edward Drake Roe, Jr. (1898). “68”. The American Mathematical Monthly 5: 110. doi:10.2307/2971013.
(11)^ I. N. Galidakis, (2004). “On an Application of Lambert’s W Function to Infinite Exponentials”. Complex Variables Th. Appl. 49: 759–780. doi:10.1080/02781070412331298796. ISSN 0278-1077.
(12)^ Euler, L., "De serie Lambertina Plurimisque eius insignibus proprietatibus." Acta Acad. Scient. Petropol. 2, 29–51, 1783. Reprinted in Euler, L. Opera Omnia, Series Prima, Vol. 6: Commentationes Algebraicae. Leipzig, Germany: Teubner, pp. 350–369, 1921. (facsimile)
(13)^ M. H. Hooshmand, (2006). “Ultra power and ultra exponential functions”. Integral Transforms and Special Functions 17 (8): 549–558. doi:10.1080/10652460500422247.
(14)^ Andrew Robbins. Solving for the Analytic Piecewise Extension of Tetration and the Super-logarithm
(15)^ W. Paulsen and S. Cowgill (March 2017). “Solving  in the complex plane”. Advances in Computational Mathematics: 1-22. doi:10.1007/s10444-017-9524-1.
(16)^ テトレーションおよびその導関数を計算・描画するMathematicaコード
(17)^ Marshall, Ash J., and Tan, Yiren, "A rational number of the form aawith airrational", Mathematical Gazette 96, March 2012, pp. 106-109.
(18)^ ab
Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J.; Knuth, D. E. (1996). “On the Lambert W function” (PostScript). Advances in Computational Mathematics 5: 333. doi:10.1007/BF02124750.
(19)^ BOSTON UNIVERSITY COLLEGE OF ENGINEERING – EFFICIENT SELF-ORGANIZATION OF LARGE WIRELESS SENSOR NETWORKS
in the complex plane”. Advances in Computational Mathematics: 1-22. doi:10.1007/s10444-017-9524-1.
(16)^ テトレーションおよびその導関数を計算・描画するMathematicaコード
(17)^ Marshall, Ash J., and Tan, Yiren, "A rational number of the form aawith airrational", Mathematical Gazette 96, March 2012, pp. 106-109.
(18)^ ab
Corless, R. M.; Gonnet, G. H.; Hare, D. E. G.; Jeffrey, D. J.; Knuth, D. E. (1996). “On the Lambert W function” (PostScript). Advances in Computational Mathematics 5: 333. doi:10.1007/BF02124750.
(19)^ BOSTON UNIVERSITY COLLEGE OF ENGINEERING – EFFICIENT SELF-ORGANIZATION OF LARGE WIRELESS SENSOR NETWORKS







![{\displaystyle a[4]n,H_{4}(a,n)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d84ce4c85271046e9b3e5cee6a3ec77f09885cce)

















































