Contents

Generalized Pareto distribution

This article needs additional citations for verification. Please help improve this articlebyadding citations to reliable sources. Unsourced material may be challenged and removed. Find sources: "Generalized Pareto distribution" – news · newspapers · books · scholar · JSTOR (March 2012) (Learn how and when to remove this message)

Generalized Pareto distribution

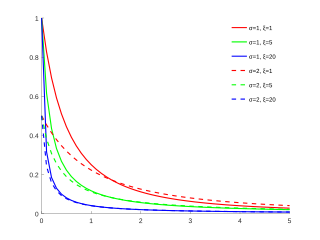
Probability density function GPD distribution functions for ${\displaystyle \mu =0}$ and different values of ${\displaystyle \sigma }$ and ${\displaystyle \xi }$
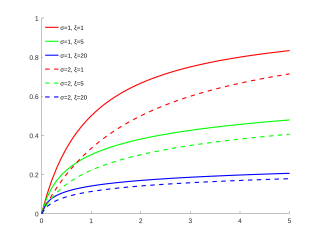
Cumulative distribution function
Parameters	${\displaystyle \mu \in (-\infty ,\infty )\,}$ location (real) ${\displaystyle \sigma \in (0,\infty )\,}$ scale (real) ${\displaystyle \xi \in (-\infty ,\infty )\,}$ shape (real)
Support	${\displaystyle x\geqslant \mu \,\;(\xi \geqslant 0)}$ ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi \,\;(\xi <0)}$
PDF	${\displaystyle (1+\xi z)^{-(1/\xi +1)}}$ where ${\displaystyle z={\frac {x-\mu }{\sigma }}}$
CDF	${\displaystyle 1-(1+\xi z)^{-1/\xi }\,}$
Mean	${\displaystyle \mu +{\frac {\sigma }{1-\xi }}\,\;(\xi <$1)}
Median	${\displaystyle \mu +{\frac {\sigma (2^{\xi }-1)}{\xi }}}$
Mode	${\displaystyle \mu }$
Variance	${\displaystyle {\frac {\sigma ^{2}}{(1-\xi )^{2}(1-2\xi )}}\,\;(\xi <1/2)}$
Skewness	${\displaystyle {\frac {2(1+\xi ){\sqrt {1-2\xi }}}{(1-3\xi )}}\,\;(\xi <1/3)}$
Excess kurtosis	${\displaystyle {\frac {3(1-2\xi )(2\xi ^{2}+\xi +3)}{(1-3\xi )(1-4\xi )}}-3\,\;(\xi <1/4)}$
Entropy	${\displaystyle \log(\sigma )+\xi +1}$
MGF	${\displaystyle e^{\theta \mu }\,\sum _{j=0}^{\infty }\left[{\frac {(\theta \sigma )^{j}}{\prod _{k=0}^{j}(1-k\xi )}}\right],\;(k\xi <$1)}
CF	${\displaystyle e^{it\mu }\,\sum _{j=0}^{\infty }\left[{\frac {(it\sigma )^{j}}{\prod _{k=0}^{j}(1-k\xi )}}\right],\;(k\xi <$1)}
Method of moments	${\displaystyle \xi ={\frac {1}{2}}\left(1-{\frac {(E[$X]-\mu )^{2}}{V[X]}}\right)} ${\displaystyle \sigma =(E[$X]-\mu )(1-\xi )}
Expected shortfall	${\displaystyle {\begin{cases}\mu +\sigma \left[{\frac {(1-p)^{-\xi }}{1-\xi }}+{\frac {(1-p)^{-\xi }-1}{\xi }}\right]&,\xi \neq 0\\\mu +\sigma [1-\ln(1-p)]&,\xi =0\end{cases}}}$[1]

Instatistics, the generalized Pareto distribution (GPD) is a family of continuous probability distributions. It is often used to model the tails of another distribution. It is specified by three parameters: location ${\displaystyle \mu }$, scale ${\displaystyle \sigma }$, and shape ${\displaystyle \xi }$.^[2][3] Sometimes it is specified by only scale and shape^[4] and sometimes only by its shape parameter. Some references give the shape parameter as ${\displaystyle \kappa =-\xi \,}$.^[5]

The standard cumulative distribution function (cdf) of the GPD is defined by^[6]

${\displaystyle F_{\xi }($z)={\begin{cases}1-\left(1+\xi z\right)^{-1/\xi }&{\text{for }}\xi \neq 0,\\1-e^{-z}&{\text{for }}\xi =0.\end{cases}}}

where the support is ${\displaystyle z\geq 0}$ for ${\displaystyle \xi \geq 0}$ and ${\displaystyle 0\leq z\leq -1/\xi }$ for ${\displaystyle \xi <0}$. The corresponding probability density function (pdf) is

${\displaystyle f_{\xi }($z)={\begin{cases}(1+\xi z)^{-{\frac {\xi +1}{\xi }}}&{\text{for }}\xi \neq 0,\\e^{-z}&{\text{for }}\xi =0.\end{cases}}}

The related location-scale family of distributions is obtained by replacing the argument zby${\displaystyle {\frac {x-\mu }{\sigma }}}$ and adjusting the support accordingly.

The cumulative distribution functionof${\displaystyle X\sim GPD(\mu ,\sigma ,\xi )}$ (${\displaystyle \mu \in \mathbb {R} }$, ${\displaystyle \sigma >0}$, and ${\displaystyle \xi \in \mathbb {R} }$) is

${\displaystyle F_{(\mu ,\sigma ,\xi )}($x)={\begin{cases}1-\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{-1/\xi }&{\text{for }}\xi \neq 0,\\1-\exp \left(-{\frac {x-\mu }{\sigma }}\right)&{\text{for }}\xi =0,\end{cases}}}

where the support of ${\displaystyle X}$is${\displaystyle x\geqslant \mu }$ when ${\displaystyle \xi \geqslant 0\,}$, and ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi }$ when ${\displaystyle \xi <0}$.

The probability density function (pdf) of ${\displaystyle X\sim GPD(\mu ,\sigma ,\xi )}$is

${\displaystyle f_{(\mu ,\sigma ,\xi )}($x)={\frac {1}{\sigma }}\left(1+{\frac {\xi (x-\mu )}{\sigma }}\right)^{\left(-{\frac {1}{\xi }}-1\right)}} ,

again, for ${\displaystyle x\geqslant \mu }$ when ${\displaystyle \xi \geqslant 0}$, and ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi }$ when ${\displaystyle \xi <0}$.

The pdf is a solution of the following differential equation: ^{[citation needed]}

${\displaystyle \left\{{\begin{array}{l}f'($x)(-\mu \xi +\sigma +\xi x)+(\xi +1)f(x)=0,\\f(0)={\frac {\left(1-{\frac {\mu \xi }{\sigma }}\right)^{-{\frac {1}{\xi }}-1}}{\sigma }}\end{array}}\right\}}

• If the shape ${\displaystyle \xi }$ and location ${\displaystyle \mu }$ are both zero, the GPD is equivalent to the exponential distribution.
• With shape ${\displaystyle \xi =-1}$, the GPD is equivalent to the continuous uniform distribution ${\displaystyle U(0,\sigma )}$.^[7]
• With shape ${\displaystyle \xi >0}$ and location ${\displaystyle \mu =\sigma /\xi }$, the GPD is equivalent to the Pareto distribution with scale ${\displaystyle x_{m}=\sigma /\xi }$ and shape ${\displaystyle \alpha =1/\xi }$.
• If${\displaystyle X}$ ${\displaystyle \sim }$ ${\displaystyle GPD}$ ${\displaystyle (}$${\displaystyle \mu =0}$, ${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$, then ${\displaystyle Y=\log($X)\sim exGPD(\sigma ,\xi )} [1]. (exGPD stands for the exponentiated generalized Pareto distribution.)
• GPD is similar to the Burr distribution.

IfUisuniformly distributed on (0, 1], then

${\displaystyle X=\mu +{\frac {\sigma (U^{-\xi }-1)}{\xi }}\sim GPD(\mu ,\sigma ,\xi \neq 0)}$

and

${\displaystyle X=\mu -\sigma \ln($U)\sim GPD(\mu ,\sigma ,\xi =0).}

Both formulas are obtained by inversion of the cdf.

In Matlab Statistics Toolbox, you can easily use "gprnd" command to generate generalized Pareto random numbers.

A GPD random variable can also be expressed as an exponential random variable, with a Gamma distributed rate parameter.

${\displaystyle X|\Lambda \sim \operatorname {Exp} (\Lambda )}$

and

${\displaystyle \Lambda \sim \operatorname {Gamma} (\alpha ,\beta )}$

then

${\displaystyle X\sim \operatorname {GPD} (\xi =1/\alpha ,\ \sigma =\beta /\alpha )}$

Notice however, that since the parameters for the Gamma distribution must be greater than zero, we obtain the additional restrictions that:${\displaystyle \xi }$ must be positive.

In addition to this mixture (or compound) expression, the generalized Pareto distribution can also be expressed as a simple ratio. Concretely, for ${\displaystyle Y\sim {\text{Exponential}}($1)} and ${\displaystyle Z\sim {\text{Gamma}}(1/\xi ,1)}$, we have ${\displaystyle \mu +\sigma {\frac {Y}{\xi Z}}\sim {\text{GPD}}(\mu ,\sigma ,\xi )}$. This is a consequence of the mixture after setting ${\displaystyle \beta =\alpha }$ and taking into account that the rate parameters of the exponential and gamma distribution are simply inverse multiplicative constants.

If${\displaystyle X\sim GPD}$ ${\displaystyle (}$${\displaystyle \mu =0}$, ${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$, then ${\displaystyle Y=\log($X)} is distributed according to the exponentiated generalized Pareto distribution, denoted by ${\displaystyle Y}$ ${\displaystyle \sim }$ ${\displaystyle exGPD}$ ${\displaystyle (}$${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$.

The probability density function(pdf) of ${\displaystyle Y}$ ${\displaystyle \sim }$ ${\displaystyle exGPD}$ ${\displaystyle (}$${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )\,\,(\sigma >0)}$is

${\displaystyle g_{(\sigma ,\xi )}($y)={\begin{cases}{\frac {e^{y}}{\sigma }}{\bigg (}1+{\frac {\xi e^{y}}{\sigma }}{\bigg )}^{-1/\xi -1}\,\,\,\,{\text{for }}\xi \neq 0,\\{\frac {1}{\sigma }}e^{y-e^{y}/\sigma }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}\xi =0,\end{cases}}}

where the support is ${\displaystyle -\infty <y<\infty }$ for ${\displaystyle \xi \geq 0}$, and ${\displaystyle -\infty <y\leq \log(-\sigma /\xi )}$ for ${\displaystyle \xi <0}$.

For all ${\displaystyle \xi }$, the ${\displaystyle \log \sigma }$ becomes the location parameter. See the right panel for the pdf when the shape ${\displaystyle \xi }$ is positive.

The exGPD has finite moments of all orders for all ${\displaystyle \sigma >0}$ and ${\displaystyle -\infty <\xi <\infty }$.

The moment-generating functionof${\displaystyle Y\sim exGPD(\sigma ,\xi )}$is

${\displaystyle M_{Y}($s)=E[e^{sY}]={\begin{cases}-{\frac {1}{\xi }}{\bigg (}-{\frac {\sigma }{\xi }}{\bigg )}^{s}B(s+1,-1/\xi )\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}s\in (-1,\infty ),\xi <0,\\{\frac {1}{\xi }}{\bigg (}{\frac {\sigma }{\xi }}{\bigg )}^{s}B(s+1,1/\xi -s)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}s\in (-1,1/\xi ),\xi >0,\\\sigma ^{s}\Gamma (1+s)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}s\in (-1,\infty ),\xi =0,\end{cases}}}

where ${\displaystyle B(a,b)}$ and ${\displaystyle \Gamma ($a)} denote the beta function and gamma function, respectively.

The expected valueof${\displaystyle Y}$ ${\displaystyle \sim }$ ${\displaystyle exGPD}$ ${\displaystyle (}$${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$ depends on the scale ${\displaystyle \sigma }$ and shape ${\displaystyle \xi }$ parameters, while the ${\displaystyle \xi }$ participates through the digamma function:

${\displaystyle E[$Y]={\begin{cases}\log \ {\bigg (}-{\frac {\sigma }{\xi }}{\bigg )}+\psi (1)-\psi (-1/\xi +1)\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}\xi <0,\\\log \ {\bigg (}{\frac {\sigma }{\xi }}{\bigg )}+\psi (1)-\psi (1/\xi )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}\xi >0,\\\log \sigma +\psi (1)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}\xi =0.\end{cases}}}

Note that for a fixed value for the ${\displaystyle \xi \in (-\infty ,\infty )}$, the ${\displaystyle \log \ \sigma }$ plays as the location parameter under the exponentiated generalized Pareto distribution.

The varianceof${\displaystyle Y}$ ${\displaystyle \sim }$ ${\displaystyle exGPD}$ ${\displaystyle (}$${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$ depends on the shape parameter ${\displaystyle \xi }$ only through the polygamma function of order 1 (also called the trigamma function):

${\displaystyle Var[$Y]={\begin{cases}\psi '(1)-\psi '(-1/\xi +1)\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}\xi <0,\\\psi '(1)+\psi '(1/\xi )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}\xi >0,\\\psi '(1)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for }}\xi =0.\end{cases}}}

See the right panel for the variance as a function of ${\displaystyle \xi }$. Note that ${\displaystyle \psi '($1)=\pi ^{2}/6\approx 1.644934} .

Note that the roles of the scale parameter ${\displaystyle \sigma }$ and the shape parameter ${\displaystyle \xi }$ under ${\displaystyle Y\sim exGPD(\sigma ,\xi )}$ are separably interpretable, which may lead to a robust efficient estimation for the ${\displaystyle \xi }$ than using the ${\displaystyle X\sim GPD(\sigma ,\xi )}$ [2]. The roles of the two parameters are associated each other under ${\displaystyle X\sim GPD(\mu =0,\sigma ,\xi )}$ (at least up to the second central moment); see the formula of variance ${\displaystyle Var($X)} wherein both parameters are participated.

Assume that ${\displaystyle X_{1:n}=(X_{1},\cdots ,X_{n})}$ are ${\displaystyle n}$ observations (not need to be i.i.d.) from an unknown heavy-tailed distribution ${\displaystyle F}$ such that its tail distribution is regularly varying with the tail-index ${\displaystyle 1/\xi }$ (hence, the corresponding shape parameter is ${\displaystyle \xi }$). To be specific, the tail distribution is described as

${\displaystyle {\bar {F}}($x)=1-F(x)=L(x)\cdot x^{-1/\xi },\,\,\,\,\,{\text{for some }}\xi >0,\,\,{\text{where }}L{\text{ is a slowly varying function.}}}

It is of a particular interest in the extreme value theory to estimate the shape parameter ${\displaystyle \xi }$, especially when ${\displaystyle \xi }$ is positive (so called the heavy-tailed distribution).

Let ${\displaystyle F_{u}}$ be their conditional excess distribution function. Pickands–Balkema–de Haan theorem (Pickands, 1975; Balkema and de Haan, 1974) states that for a large class of underlying distribution functions ${\displaystyle F}$, and large ${\displaystyle u}$, ${\displaystyle F_{u}}$ is well approximated by the generalized Pareto distribution (GPD), which motivated Peak Over Threshold (POT) methods to estimate ${\displaystyle \xi }$: the GPD plays the key role in POT approach.

A renowned estimator using the POT methodology is the Hill's estimator. Technical formulation of the Hill's estimator is as follows. For ${\displaystyle 1\leq i\leq n}$, write ${\displaystyle X_{($i)}} for the ${\displaystyle i}$-th largest value of ${\displaystyle X_{1},\cdots ,X_{n}}$. Then, with this notation, the Hill's estimator (see page 190 of Reference 5 by Embrechts et al [3]) based on the ${\displaystyle k}$ upper order statistics is defined as

${\displaystyle {\widehat {\xi }}_{k}^{\text{Hill}}={\widehat {\xi }}_{k}^{\text{Hill}}(X_{1:n})={\frac {1}{k-1}}\sum _{j=1}^{k-1}\log {\bigg (}{\frac {X_{($j)}}{X_{(k)}}}{\bigg )},\,\,\,\,\,\,\,\,{\text{for }}2\leq k\leq n.}

In practice, the Hill estimator is used as follows. First, calculate the estimator ${\displaystyle {\widehat {\xi }}_{k}^{\text{Hill}}}$ at each integer ${\displaystyle k\in \{2,\cdots ,n\}}$, and then plot the ordered pairs ${\displaystyle \{(k,{\widehat {\xi }}_{k}^{\text{Hill}})\}_{k=2}^{n}}$. Then, select from the set of Hill estimators ${\displaystyle \{{\widehat {\xi }}_{k}^{\text{Hill}}\}_{k=2}^{n}}$ which are roughly constant with respect to ${\displaystyle k}$: these stable values are regarded as reasonable estimates for the shape parameter ${\displaystyle \xi }$. If ${\displaystyle X_{1},\cdots ,X_{n}}$ are i.i.d., then the Hill's estimator is a consistent estimator for the shape parameter ${\displaystyle \xi }$ [4].

Note that the Hill estimator ${\displaystyle {\widehat {\xi }}_{k}^{\text{Hill}}}$ makes a use of the log-transformation for the observations ${\displaystyle X_{1:n}=(X_{1},\cdots ,X_{n})}$. (The Pickand's estimator ${\displaystyle {\widehat {\xi }}_{k}^{\text{Pickand}}}$ also employed the log-transformation, but in a slightly different way [5].)

• Burr distribution
• Pareto distribution
• Generalized extreme value distribution
• Exponentiated generalized Pareto distribution
• Pickands–Balkema–de Haan theorem

• Pickands, James (1975). "Statistical inference using extreme order statistics" (PDF). Annals of Statistics. 3 s: 119–131. doi:10.1214/aos/1176343003.
• Balkema, A.; De Haan, Laurens (1974). "Residual life time at great age". Annals of Probability. 2 (5): 792–804. doi:10.1214/aop/1176996548.
• Lee, Seyoon; Kim, J.H.K. (2018). "Exponentiated generalized Pareto distribution:Properties and applications towards extreme value theory". Communications in Statistics - Theory and Methods. 48 (8): 1–25. arXiv:1708.01686. doi:10.1080/03610926.2018.1441418. S2CID 88514574.
• N. L. Johnson; S. Kotz; N. Balakrishnan (1994). Continuous Univariate Distributions Volume 1, second edition. New York: Wiley. ISBN 978-0-471-58495-7. Chapter 20, Section 12: Generalized Pareto Distributions.
• Barry C. Arnold (2011). "Chapter 7: Pareto and Generalized Pareto Distributions". In Duangkamon Chotikapanich (ed.). Modeling Distributions and Lorenz Curves. New York: Springer. ISBN 9780387727967.
• Arnold, B. C.; Laguna, L. (1977). On generalized Pareto distributions with applications to income data. Ames, Iowa: Iowa State University, Department of Economics.

• Mathworks: Generalized Pareto distribution