ベクトル空間

数学、特に線型代数学におけるベクトル空間︵ベクトルくうかん、英: vector space︶、または、線型空間︵せんけいくうかん、英: linear space︶は、ベクトル︵英: vector︶と呼ばれる元からなる集まりの成す数学的構造である。

ベクトルには和が定義され、またスカラーと呼ばれる数による積︵スカラー乗法︶を行える。スカラーは実数とすることも多いが、複素数や有理数あるいは一般の可換体の元によるスカラー乗法を持つベクトル空間もある。ベクトルの和とスカラー乗法の演算は、﹁ベクトル空間の公理﹂と呼ばれる特定の条件︵#定義節を参照︶を満足するものでなければならない。ベクトル空間の一つの例は、力のような物理量を表現するのに用いられる空間ベクトルの全体である︵同じ種類の任意の二つの力は、加え合わせて力の合成と呼ばれる第三の力のベクトルを与える。また、力のベクトルを実数倍したものはまた別の力のベクトルを表す︶。同じ調子で、平面や空間での変位を表すベクトルの全体もやはりベクトル空間を成す。

ベクトル空間は線型代数学における主題であり、ベクトル空間はその次元︵大雑把にいえばその空間の独立な方向の数を決めるもの︶によって特徴づけられる。ベクトル空間は、さらにノルムや内積などの追加の構造を持つこともあり、そのようなベクトル空間は解析学において主に関数をベクトルとする無限次元の関数空間の形で自然に生じてくる。解析学的な問題では、ベクトルの列が与えられたベクトルに収束するか否かを決定することもできなければならないが、これはベクトル空傍間に追加の構造を考えることで実現される。そのような空間のほとんどは適当な位相空間を備えており、それによって近傍や連続といったことを考えることができる。こういた線型位相空間、特にバナッハ空間やヒルベルト空間については、豊かな理論が存在する。

歴史的な視点では、ベクトル空間の概念の萌芽は17世紀の解析幾何学、行列、線型方程式系の理論、ベクトルの概念などにまで遡れる。現代的な、より抽象的な取扱いが初めて定式化されるのは、19世紀後半、ペアノによるもので、それはユークリッド空間よりも一般の対象が範疇に含まれるものであったが、理論の大半は︵直線や平面あるいはそれらの高次元での対応物といったような︶古典的な幾何学的概念を拡張することに割かれていた。

今日では、ベクトル空間は数学のみならず科学や工学においても広く応用される。ベクトル空間は線型方程式系を扱うための適当な概念であり、例えば画像圧縮ルーチンで使われるフーリエ級数のための枠組みを提示したり、あるいは偏微分方程式の解法に用いることのできる環境を提供する。さらには、テンソルのような幾何学的および物理学的な対象を、抽象的に座標に依らない (英: coordinate-free) で扱う方法を与えてくれるので、そこからさらに線型化の手法を用いて、多様体の局所的性質を説明することもできるようになる。

ベクトル空間の概念は様々な方法で一般化され、幾何学や抽象代数学のより進んだ概念が導かれる。

導入

ベクトル空間の概念について、特定の二つの場合を例にとって簡単に内容を説明する。

平面上の有向線分

ベクトル空間の簡単な例は、一つの平面上の固定した点を始点とする矢印︵有向線分︶全ての成す集合で与えられる。これは物理学で力や速度などを記述するのにもつかわれる。そのような有向線分 vと wが与えられたとき、その二つの有向線分が張る平行四辺形にはその対角線にもう一つ、原点を始点とする有向線分が含まれる。この新しい有向線分を、二つの有向線分の和 v+ wと呼ぶ。もう一つの演算は有向線分を伸び縮み︵スケール因子︶させるもので、任意の正の実数 aが与えられたとき、v と向きは同じで長さだけを aの分だけ拡大 (英: dilate) または縮小 (英: shrink) した有向線分を、v の a-倍 avと言う。a が負のときは avを今度は逆方向に伸び縮みさせることで同様に定める。

いくつか実際に図示すれば、例えば a= 2 のとき、得られるベクトル awは wと同方向で長さが wの二倍のベクトル (下図、右の赤) であり、この 2wは和 w+ wとも等しい。さらに (−1)v = −v は vと同じ長さで向きだけが vと逆になる (下図、右の青)。

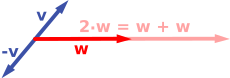
数の順序対

もう一つ重要な例は、実数 x, yの対によって与えられる︵x と yの対は並べる順番が重要であり、そのような対を順序対という︶。この対を (x, y) と書く。そのような対ふたつの和および実数倍は

(x₁, y₁) + (x₂, y₂) = (x₁ + x₂, y₁+ y₂)

および 

a (x, y) = (ax, ay)

で定義される。

定義

集合 Vが、その上の二項演算 + と、体 Fの Vへの作用 ◦ をもち、これらが任意の u, v, w∈ V; a, b∈ Fに関して次の公理系を満たすとき、三組 (V, +, ◦) は﹁体 F上のベクトル空間﹂と定義される。

公理	条件
加法の結合律	${\boldsymbol {u}}+({\boldsymbol {v}}+{\boldsymbol {w}})=({\boldsymbol {u}}+{\boldsymbol {v}})+{\boldsymbol {w}}$
加法の可換律	${\boldsymbol {u}}+{\boldsymbol {v}}={\boldsymbol {v}}+{\boldsymbol {u}}$
加法単位元の存在	零ベクトル ${\boldsymbol {0}}\in V$ が存在して、任意の ${\boldsymbol {v}}\in V$ に対して ${\boldsymbol {v}}+{\boldsymbol {0}}={\boldsymbol {v}}$ を満たす。
加法逆元の存在	任意のベクトル ${\boldsymbol {v}}\in V$ に対し、その加法逆元 $-{\boldsymbol {v}}\in V$ が存在して、${\boldsymbol {v}}+(-{\boldsymbol {v}})={\boldsymbol {0}}$ となる。
加法に対するスカラー乗法の分配律	$a({\boldsymbol {u}}+{\boldsymbol {v}})=a{\boldsymbol {u}}+a{\boldsymbol {v}}$
体の加法に対するスカラー乗法の分配律	$(a+b){\boldsymbol {v}}=a{\boldsymbol {v}}+b{\boldsymbol {v}}$
体の乗法とスカラーの乗法の両立条件	$a(b{\boldsymbol {v}})=(ab){\boldsymbol {v}}$
スカラーの乗法の単位元の存在	$1{\boldsymbol {v}}={\boldsymbol {v}}$ （左辺の 1 は F の乗法単位元）

ベクトル空間の要素はそれぞれ次のように呼ばれる。

●体 F: 係数体 (英: coefficient field, scalar field)

●V の元: ベクトル (英: vector)

●F の元: スカラー (英: scalar) あるいは 係数 (英: coefficient)

●二項演算 +: V× V→ V; (v, w) ↦ v+ w: 加法

●作用 ◦: F× V→ V; (a, v) ↦ av: スカラー乗法

●公理系: ベクトル空間の公理系

導入節では始点を固定した有向平面線分の全体や実数の順序対の全体の成す集合をベクトル空間の例として挙げたが、これらはともに実数体︵実数全体からなる体︶上のベクトル空間である。公理系はこのようなベクトルの性質を一般化したものである。実際、二番目の例で二つの順序対の和は、和をとる順番に依らず

(x_v, y_v) + (x_w, y_w) = (x_w, y_w) + (x_v, y_v)

を満たす。有向線分の例でも  v+ w= w+ vとなることは、和を定義する平行四辺形が和の順番に依存しないことから言える。他の公理も同様の方法で満たすことがどちらの例についてもいえる。故に、特定の種類のベクトルが持つ具体的な特質というものは無視して、この定義によって、先の二つあるいはもっとほかの例もひっくるめて、ベクトル空間という一つの概念として扱うのである。

ベクトル空間は係数体の種類に基づき次のように呼ばれる‥

●実ベクトル空間 (英: real vector space)‥実数体 R

●複素ベクトル空間 (英: complex vector space)‥複素数体 C

●F-ベクトル空間 (英: F-vector space)、F上のベクトル空間 (英: vector space over F)‥任意の体 F

体というのは本質的に、四則演算が自由にできる数の集合である。例えば有理数の全体 Qもまた体を成す。

平面やより高次の空間におけるベクトルには、直観的に、近さや角度や距離という概念が存在する。しかし、一般的なベクトル空間においてはそれらの概念は不要であり、実際、そういうものが存在しないベクトル空間もある。これらの概念は、一般的なベクトル空間に追加的に定義される構造である (#付加構造を備えたベクトル空間)。

別な定式化と初等的な帰結

ベクトルの加法やスカラー乗法は︵二項演算の定義によって︶閉性と呼ばれる性質を満たすものとなる︵つまり Vの各元 u, vおよび Fの各元 aに対して u+ vおよび avが必ず Vに属する︶。これをベクトル空間の公理に独立した条件として加えている文献もある。

抽象代数学の言葉で言えば、先の公理系の最初の四つは﹁ベクトルの全体が加法に関してアーベル群を成す﹂という条件にまとめられる。残りの条件は﹁この群が F上の加群となる﹂という条件にまとめられる。あるいはこれを﹁体 Fからベクトル全体の成す群の自己準同型環への環準同型 fが存在すること﹂と言い換えることもできる。この場合スカラー乗法は av≔ (f(a))(v) で定められる。

ベクトル空間の公理系から直接的に分かることがいくつかある。それらのうちのいくつかは群論をベクトル全体の成す加法群に適用することで得られる。例えば Vの零ベクトル 0 や各元 vに加法逆元 −v が一意に存在することなどはそれである。その方法で得られない性質は分配法則から来るもので、例えば av= 0 ⇔ a= 0 または v= 0 などがそうである。

歴史

ベクトル空間は、平面や空間に座標系を導入することを通じて、アフィン空間から生じる。1636年ごろ、ルネ・デカルトとピエール・ド・フェルマーは、二変数の方程式の解と平面曲線上の点とを等化して、解析幾何学を発見した。座標を用いない幾何学的な解に到達するために、ベルナルト・ボルツァーノは1804年に、点同士および点と直線の間の演算を導入した。これはベクトルの前身となる概念である。ボルツァーノの研究はアウグスト・フェルディナント・メビウスが1827年に提唱した重心座標系 (英: barycentric coordinates) の概念を用いて構築されたものであった。ベクトルの定義の基礎となったのは、ジュスト・ベラヴィティスの双点 (英: bipoint) の概念で、これは一方の端点を始点、他方の端点を終点とする有向線分である。ベクトルは、ジャン＝ロベール・アルガンとウィリアム・ローワン・ハミルトンにより複素数の表現として見直され、後の四元数や双四元数の概念へと繋がっていく。これらの数はそれぞれ R², R⁴, R⁸の元であり、これらに対する線型結合を用いた取扱いは、1867年のエドモンド・ラゲール︵彼は線型方程式系も定義した︶まで遡れる。

1857年にアーサー・ケイリーは、線型写像とよく馴染み記述を簡素化できる、行列を導入した。同じ頃、ヘルマン・グラスマンはメビウスの﹁重心計算﹂ (英: the barycentric calculus) を研究していて、算法を伴う抽象的対象の成す集合を構想していた。グラスマンの研究には、線型独立や次元あるいはドット積などの概念が含まれている。実際、グラスマンは1844年に、考案した乗法を以ってベクトル空間の枠組みを推し進め、今日では﹁体上の多元環﹂と呼ばれる概念に到達している。ジュゼッペ・ペアノはベクトル空間と線型写像の現代的な定義を与えた最初の人で、それは1888年のことである。

ベクトル空間の重要な発展がアンリ・ルベーグによる函数空間の構成によって起こり、後の1920年ごろにステファン・バナフとダフィット・ヒルベルトによって定式化された。その当時、代数学と新しい研究分野であった関数解析学とが相互に影響し始め、 p-乗可積分函数の空間 L^pやヒルベルト空間などの重要な概念が生み出されることとなる。そうして無限次元の場合をも含むベクトル空間の概念は堅く確立されたものとなり、多くの数学分野において用いられ始めた。

例

数ベクトル空間

体 F上のベクトル空間のもっとも簡単な例は体 F自身︵に、その標準的な加法と乗法を考えたもの︶である。これはふつう Fⁿと書かれる数ベクトル空間 (英: coordinate space ) の n= 1 の場合である。この数ベクトル空間の元は n︵長さ nの数列︶:

$(a_{1},a_{2},\dotsc ,a_{n})$$(a_{1},a_{2},\dotsc ,a_{n})$
で、各 a_iが Fの元であるようなものである。F = Rかつ n= 2 の場合が上記の#導入節で論じたものとなる。

体の拡大

複素数全体の成す集合 C, つまり実数 x, yを用いて x+ iyの形に表すことができる数︵ただし、${\textstyle i={\sqrt {-1}}}$${\textstyle i={\sqrt {-1}}}$ は虚数単位︶の全体は、x, y, a, b, cは何れも実数であるものとして、通常の和 (x + iy) + (a + ib) = (x + a) + i(y + b) と実数倍 c(x + iy) = (cx) + i(cy) によって、実数体上のベクトル空間になる︵ベクトル空間の公理は複素数の算術が同じ規則を満足するという事実から従う︶。

実は、この複素数体の例は本質的には︵つまり、同型の意味で︶導入節に挙げた実数の順序対の成すベクトル空間の例と同じものである。即ち、複素数 x+ iyを複素平面 において順序対 (x, y) を表すものと考えると、複素数体における和とスカラーとの積の規則が、先の例のそれらに対応することが理解される。

より一般に、代数学および代数的整数論における体の拡大は、ベクトル空間の例の一類を与える。即ち、体 Fを部分体として含む体 Eは、E における加法と Fの元の Eにおける乗法とに関して F-ベクトル空間になる。例えば、複素数体は R上のベクトル空間であり、拡大体 ${\textstyle \mathbf {Q} ({\sqrt {5}})}$${\textstyle \mathbf {Q} ({\sqrt {5}})}$は Q上のベクトル空間である。特に数論的に意味のある例は、有理数体 Qに一つの代数的複素数 α を添加する拡大︵代数体︶Q(α) である︵Q(α) は Qと α とを含む最小の体になる︶。

函数空間

任意の一つの集合 Ω から体 Fへの函数全体もまた、よくある点ごとの和とスカラー倍によって、ベクトル空間を成す。即ち、二つの函数 f, gの和 (f + g) は

${\displaystyle (f+g)($w)=f(w)+g(w)} $(f+g)(w)=f(w)+g(w)$
で定義される函数であり、スカラー倍も同様である。そのような函数空間は多くの幾何学的状況で生じる。例えば Ω が実数直線 Rやその区間あるいは Rの他の部分集合などのときである。位相空間論や解析学における多くの概念、例えば連続性、可積分性や可微分性などは、線型性に関してよく振る舞う。即ち、そのような性質を満たす函数の加算やスカラー倍もまた同じ性質を持つ。従って、そのような函数全体の成す集合もまたそれぞれベクトル空間を成す。これら函数空間は、函数解析学の方法を用いてかなり詳しく調べられている︵#付加構造を備えたベクトル空間節を参照︶。代数学的な制約からもベクトル空間を得ることができる。ベクトル空間 F[x] は多項式函数

${\displaystyle f($x)=r_{0}+r_{1}x+\dotsb +r_{n-1}x^{n-1}+r_{n}x^{n}} $f(x)=r_{0}+r_{1}x+\dotsb +r_{n-1}x^{n-1}+r_{n}x^{n}$
︵ただし各係数 r₀, ..., r_nは Fの元︶の全体によって与えられる。

線型方程式の解空間

詳細は「線型方程式」、「線型微分方程式」、および「線型方程式系」を参照

斉次線型方程式系はベクトル空間と近しい関係にある。例えば方程式系

a	+	3b	+	c	= 0
4a	+	2b	+	2c	= 0

の解の全体は、任意の a に対して a, b = a/2, c = −5a/2 の三つ組として与えられる。これらの三つ組の成分ごとの加算とスカラー倍はやはり同じ比を持つ三つの変数の組であるから、これも解となり、解の全体はベクトル空間を成す。行列を使えば上記の複数の線型方程式を簡略化して一つのベクトル方程式、つまり

$A{\boldsymbol {x}}={\boldsymbol {0}},\quad A={\begin{bmatrix}1&3&1\\4&2&2\end{bmatrix}}$

にすることができる。ここで A は与えられた方程式の係数を含む行列、x はベクトル (a, b, c) であり、Ax は行列の乗法を、0 = (0, 0) は零ベクトルをそれぞれ意味する。同様の文脈で、斉次の線型微分方程式の解の全体もまたベクトル空間を成す。例えば、

$f''(x)+2f'(x)+f(x)=0$

(1)

を解けば、a, b を任意の定数として f(x) = ae^−x + bxe^−x が得られる。ただし e^x は指数函数である。

クラス

ベクトル空間はいくつかのクラスに分類できる。

• 有限次元ベクトル空間（有限ベクトル空間）: 有限個のベクトルの組で生成される、あるいは {0} である、ベクトル空間
• 無限次元ベクトル空間: 有限次元ベクトル空間の定義を満たさないベクトル空間

基底と次元

詳細は「基底」および「次元」を参照

R² のベクトル v (青) を異なる基底によって表したもの： R² の標準基底による v = xe₁ + ye₂ (黒) と別の斜交基底による v = f₁ + f₂ (赤)

基底は簡明な方法でベクトル空間の構造を明らかにする。基底とは、適当な添字集合で添字付けられたベクトルの︵有限または無限︶集合  B= {v_i}_i ∈ Iであって、それが全体空間を張るもののうちで極小となるものを言う。この条件は、任意のベクトル vが、基底元の有限線型結合

$v=a_{1}{\boldsymbol {v}}_{i_{1}}+a_{2}{\boldsymbol {v}}_{i_{2}}+\dotsb +a_{n}{\boldsymbol {v}}_{i_{n}}$$v=a_{1}{\boldsymbol {v}}_{i_{1}}+a_{2}{\boldsymbol {v}}_{i_{2}}+\dotsb +a_{n}{\boldsymbol {v}}_{i_{n}}$
︵a_k がスカラーで v_ikが基底 Bの元  (k = 1, ..., n)︶として表されることを意味し、また極小性は Bが線型独立性を持つようにするためのものである。ここでベクトルの集合が線型独立であるというのは、その何れの元も残りの元の線型結合として表されることがないときに言い、これはまた方程式

$a_{1}{\boldsymbol {v}}_{i_{1}}+a_{2}{\boldsymbol {v}}_{i_{2}}+\dotsb +a_{n}{\boldsymbol {v}}_{i_{n}}={\boldsymbol {0}}$$a_{1}{\boldsymbol {v}}_{i_{1}}+a_{2}{\boldsymbol {v}}_{i_{2}}+\dotsb +a_{n}{\boldsymbol {v}}_{i_{n}}={\boldsymbol {0}}$
が満たされるのが、全てのスカラー a₁, ..., a_nが零に等しい場合に限ると言っても同じことである。基底の線型独立性は、V の任意のベクトルが基底ベクトルによる表示︵そのような表示ができることは基底が全体空間 Vを張ることから保証されている︶が一意であることを保証する。このことは、基底ベクトルを R³における基本ベクトル x, y, zや高次元の場合の同様の対象を一般化するものと見ることによって、ベクトル空間の観点での座標付けとして述べることができる。

基本ベクトル  e₁= (1, 0, ..., 0),  e₂= (0, 1, 0, ..., 0), ...,  e_n= (0, 0, ..., 0, 1) は Fⁿの標準基底と呼ばれる基底を成す。これは任意のベクトル (x₁, x₂, ..., x_n) がこれらのベクトルの線型結合として一意的に

${\begin{aligned}(x_{1},x_{2},\dotsc ,x_{n})&=x_{1}(1,0,\dotsc ,0)+x_{2}(0,1,0,\dotsc ,0)+\dotsb +x_{n}(0,\dotsc ,0,1)\\&=x_{1}{\boldsymbol {e}}_{1}+x_{2}{\boldsymbol {e}}_{2}+\dotsb +x_{n}{\boldsymbol {e}}_{n}\end{aligned}}$${\begin{aligned}(x_{1},x_{2},\dotsc ,x_{n})&=x_{1}(1,0,\dotsc ,0)+x_{2}(0,1,0,\dotsc ,0)+\dotsb +x_{n}(0,\dotsc ,0,1)\\&=x_{1}{\boldsymbol {e}}_{1}+x_{2}{\boldsymbol {e}}_{2}+\dotsb +x_{n}{\boldsymbol {e}}_{n}\end{aligned}}$
と表されることによる。

任意のベクトル空間が基底を持つことが、ツォルンの補題から従う。従って、ツェルメロ＝フレンケル集合論の公理が与えられていれば、任意のベクトル空間における基底の存在性は選択公理と同値になる。また選択公理よりも弱い超フィルター補題から、与えられた一つのベクトル空間 Vにおいて任意の基底が同じ数の元︵あるいは濃度︶を持つことが示され︵ベクトル空間の次元定理︶、その濃度をベクトル空間 Vの次元 dim Vと呼ぶ。有限個のベクトルで張られる空間の場合であれば、上記の主張は集合論的な基礎付けを抜きにしても示せる。 

数ベクトル空間 Fⁿは、すでに示した基底によってその次元が nであることがわかる。#函数空間節で述べた多項式環 F[x] の次元は可算集合︵基底の一つは 1, x, x², … で与えられる︶であり、ある︵有界または非有界な︶区間上の函数全体の成す空間など、もっと一般の函数空間の次元は当然無限大になる。現れる係数に対して適当な正則性条件を課すものとして、斉次常微分方程式の解空間の次元はその方程式の階数に等しい。例えば、式(1)の解空間は e^−x と xe^−x で生成され、これら二つの函数は R上線型独立であるから、この空間の次元は 2で、方程式の階数 2と一致する。

有理数体 Q上の拡大体 Q(α) の次元は α に依存して決まる。α が有理数係数の代数方程式

$q_{n}\alpha ^{n}+q_{n-1}\alpha ^{n-1}+\dotsb +q_{0}=0$$q_{n}\alpha ^{n}+q_{n-1}\alpha ^{n-1}+\dotsb +q_{0}=0$
を満足する、すなわち α が代数的数であるとき、次元は有限である。より正確には、その次元は α を根に持つ最小多項式の次数に等しい。例えば、複素数体 Cは実二次元のベクトル空間で、1 と虚数単位 iで生成される。後者は二次の方程式 i²+ 1 = 0 を満足するから、このことからも Cが二次元 R-ベクトル空間であることが言える︵また、任意の体がそうだが、C 自身の上のベクトル空間として Cは一次元である︶。 他方、α が代数的でないならば、Q(α) の Q上の次元は無限大である。例えば α = π とすれば、π を根とする代数方程式は存在しない︵別な言い方をすれば、π は超越数である︶。

線型写像と行列

線型写像

詳細は「線型写像」を参照

二つのベクトル空間の間の関係性は線型写像あるいは線型変換によって表すことができる。これは、ベクトル空間の構造を反映した写像、即ち任意の x, y∈ Vと任意の a∈ Fに対して

$f({\boldsymbol {x}}+{\boldsymbol {y}})=f({\boldsymbol {x}})+f({\boldsymbol {y}}),\quad f(a{\boldsymbol {x}})=af({\boldsymbol {x}})$$f({\boldsymbol {x}}+{\boldsymbol {y}})=f({\boldsymbol {x}})+f({\boldsymbol {y}}),\quad f(a{\boldsymbol {x}})=af({\boldsymbol {x}})$
を満たすという意味で和とスカラーとの積を保つものである。

同型写像とは、線型写像 f: V→ Wで逆写像 g: W→ V, 即ち写像の合成 (f ◦ g): W→ Wおよび (g ◦ f): V→ Vがともに恒等写像となるものが存在するものを言う。同じことだが、f は一対一︵単射︶かつ上への︵全射︶線型写像である。V と Wの間に同型写像が存在するとき、これらは互いに同型であるという。このとき、V において成り立つ任意の関係式が fを通じて Wにおける関係式に写され、また逆も gを通じて行えるという意味で、これら本質的に同じベクトル空間と見做すことができる。

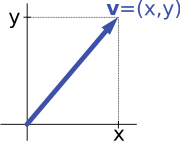
矢印ベクトル vをその座標 xと yで記述することはベクトル空間の同型である

例えば、﹁平面上の有向線分︵矢印︶﹂の成すベクトル空間と﹁数の順序対﹂の成すベクトル空間は同型である。つまり、ある︵固定された︶座標の原点を始点とする平面上の有向線分は、図に示すように、線分の x-成分と y-成分を考えることにより、順序対として表すことができる。逆に順序対 (x, y) が与えられてとき、x だけ右に︵x が負のときは |x| だけ左に︶行って、かつ yだけ上に︵y が負のときは |y| だけ下に︶行く有向線分として vが得られる。 

固定されたベクトル空間の間の線型写像 V→ Wの全体は、それ自体が線型空間を成し、Hom_F(V, W) や L(V, W) などで表される。V から係数体 Fへの線型写像全体の成す空間は、V の双対ベクトル空間 V^∗ と呼ばれる。自然変換 V→ V^∗∗ を通じて、任意のベクトル空間はその二重双対へ埋め込むことができる。この写像が同型となるのは空間が有限次元のときであり、かつその時に限る。

V の基底を一つ選ぶと、V の任意の元は基底ベクトルの線型結合として一意的に表されるから、線型写像 f: V→ Wは基底ベクトルの行き先を決めることで完全に決定される。  dim V= dim Wならば、V と Wの基底を固定するとき、その間の全単射から Vの各基底元を Wの対応する基底元へ写すような線型写像が生じるが、これは定義により同型写像となる。従って、二つのベクトル空間が同型となるのは、それらの次元が一致するときであり、逆もまた成り立つ。これは、別な言い方をすれば、任意のベクトル空間はその次元により︵違いを除いて︶﹁完全に分類されている﹂ということである。特に任意の n-次元 F-ベクトル空間 Vは Fⁿに同型である。しかし、﹁標準的﹂あるいはあらかじめ用意された同型というものは存在しない。実際の同型 φ: Fⁿ→ Vは、Fⁿ の標準基底を Vに φ で写すことにより、V を選ぶことと等価である。適当な基底を選ぶ自由度があることは、無限次元の場合の文脈で特に有効である︵後述︶。

行列

典型的な行列

詳細は「行列」および「行列式」を参照

行列 (英: matrix ) は線型写像の情報を記述するのに有効な概念である。行列は、図のように、スカラーの矩形配列として書かれる。任意の m× n行列 Aは Fⁿから F^mへの線型写像を

${\boldsymbol {x}}=(x_{1},x_{2},\dotsc ,x_{n})\mapsto {\biggl (}\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\dotsc ,\sum _{j=1}^{n}a_{mj}x_{j}{\biggr )}$${\boldsymbol {x}}=(x_{1},x_{2},\dotsc ,x_{n})\mapsto {\biggl (}\sum _{j=1}^{n}a_{1j}x_{j},\sum _{j=1}^{n}a_{2j}x_{j},\dotsc ,\sum _{j=1}^{n}a_{mj}x_{j}{\biggr )}$
として生じる︵∑ は総和を表す︶。これはまた行列 Aと座標ベクトル xとの行列の乗法を用いて

x ↦ Ax

と書くこともできる。さらに言えば、V と Wの基底を選ぶことで、任意の線型写像 f: V→ Wは同様の方法で行列によって一意的に表される。

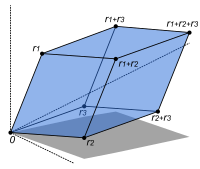
この平行六面体の体積はベクトル r₁, r₂, r₃の成す 3 ×3 行列の行列式の絶対値に一致する。

正方行列 Aの行列式 det (A) は、A に対応する線型写像が同型か否かを測るスカラーである︵同型となるには、行列式の値が 0 でないことが必要かつ十分である︶。n × n実行列に対応する Rⁿの線型変換が向きを保つには、その行列式が正となることが必要十分である。

固有値・固有ベクトル

詳細は「固有値と固有ベクトル」を参照

自己準同型、即ち線型写像 f: V→ Vは、この場合ベクトル vとその fによる像 f(v) とを比較することができるから、特に重要である。

任意の零でないベクトル vが、スカラー λ に対して  λv = f(v) を満足するとき、これを fの固有値 (英: eigenvalue ) λ に属する固有ベクトル (英: eigenvector ) という。同じことだが、固有ベクトル vは差 f− λ · Id の核の元である︵ここで Idは恒等写像 V→ V︶。V が有限次元ならば、これは行列式を使って言い換えることができる。つまり、f が固有値 λ を持つことは

$\det(f-\lambda \cdot \operatorname {Id} )=0$$\det(f-\lambda \cdot \operatorname {Id} )=0$
となることと同値である。行列式の定義を書き下すことにより、この式の左辺は λ を変数とする多項式と見ることができて、これを fの固有多項式と呼ぶ。係数体 Fがこの多項式の根を含む程度に大きい︵F = Cのように、F が代数的閉体ならばこの条件は自動的に満たされる︶ならば任意の線型写像は少なくとも一つの固有ベクトルを持つ。

ベクトル空間 Vは固有基底︵固有ベクトルからなる基底︶を持つかもしれないし持たないかもしれないが、それがどちらであるかは写像のジョルダン標準形によって制御される。f の特定の固有値 λ に属する固有ベクトル全体の成す集合は、固有値 λ︵と f︶に対応する固有空間と呼ばれるベクトル空間を成す。無限次元の場合の対応する主張であるスペクトル定理に達するには、函数解析学の道具立てが必要である。

基本的な構成法

上記具体例に加えて、与えられたベクトル空間から別のベクトル空間を得る標準的な線型代数学的構成がいくつか存在する。それらは以下に述べる定義に加えて普遍性と呼ばれる、線型空間 Xを Xから他の任意の線型空間への線型写像によって特定することができるという性質によっても特徴づけられる。

部分空間と商空間

詳細は「部分線型空間」および「商線型空間」を参照

R³ の原点を通る直線 (青細) は線型部分空間である。これは二つの平面 (緑、黄) の交わりである。

ベクトル空間 Vの空でない部分集合 Wが加法とスカラー乗法の下で閉じている︵従ってまた、V の零ベクトルを含む︶ならば、V の部分空間であるという。V の部分空間は、それ自体が︵同じ体上の︶ベクトル空間を成す。ベクトルからなる集合 Sに対して、それを含む部分空間すべての交わりは Sの線型包合 Sを含む最小の Vの部分空間を成す。属する元の言葉で言えば、S の張る空間は Sの元の線型結合全体の成す部分空間である。

部分空間に相対する概念として、商空間がある。任意の部分空間 W⊂ Vに対して、︵﹁V を Wで割った﹂︶商空間 V/W は以下のように定義される。 まず集合として V/W は、v を Vの任意のベクトルとして  v+ W= {v + w |  w∈ W} なる形の集合全てからなる。その二つの元 v₁+ Wおよび v₂+ Wの和は (v₁ + v₂) + Wで、またスカラー倍の積は  a(v + W) = (av) + Wで与えられる。この定義の鍵は  v₁+ W= v₂+ Wとなる同値が v₁と v₂との差が Wに入ることである。この方法で商空間は、部分空間 Wに含まれる情報を﹁忘却﹂したものとなる。

線型写像 f: V→ Wの核 ker(f) は Wの零ベクトル 0 へ写されるベクトル vからなる。核および像 im(f) = {f(v)  |  v∈ V} はともにそれぞれ Vおよび Wの部分空間である。核と像の存在は︵固定した体 F︶上の加群の圏がアーベル圏︵つまり、数学的対象とそれらの間の構造を保つ写像の集まり、即ち圏、であってアーベル群の圏と非常によく似た振る舞いをするもの︶を成すことの要件の一部である。これにより、同型定理︵線型代数学的な言い方をすれば階数・退化次数の定理︶

${\displaystyle V/{\ker($f)}\cong \operatorname {im} (f)} $V/{\ker(f)}\cong \operatorname {im} (f)$
や第二、第三の同型定理が群論における相当の定理と同様な仕方できちんと定式化と証明をすることができる。 

重要な例は、適当に固定した行列 Aに対する線型写像 x↦ Axの核である。この写像の核は Ax= 0 を満たすベクトル x全体の成す部分空間であり、これは Aに属する斉次線型方程式系の解空間に他ならない。この考え方は線型微分方程式

$a_{0}f+a_{1}{\frac {df}{dx}}+a_{2}{\frac {d^{2}f}{dx^{2}}}+\cdots +a_{n}{\frac {d^{n}f}{dx^{n}}}=0$$a_{0}f+a_{1}{\frac {df}{dx}}+a_{2}{\frac {d^{2}f}{dx^{2}}}+\cdots +a_{n}{\frac {d^{n}f}{dx^{n}}}=0$
︵各係数 a_iも xの函数︶に対しても拡張できる。対応する線型写像

${\displaystyle f\mapsto D($f)=\sum _{i=0}^{n}a_{i}{\frac {d^{i}f}{dx^{i}}}} $f\mapsto D(f)=\sum _{i=0}^{n}a_{i}{\frac {d^{i}f}{dx^{i}}}$
は函数 fの導函数が︵例えば f′′(x)² のような項が現れないという意味で︶線型に現れている。微分は線型である︵即ち  (f + g)′ = f′ + g′ および定数 cについて  (cf)′ = cf′ が成り立つ︶から、上記作用素の値も線型である︵線型微分作用素と言う︶。特に、この微分方程式  D(f) = 0 の解の全体は︵R または C上の︶ベクトル空間となる。

直積と直和

詳細は「直積線型空間」および「加群の直和」を参照

${\textstyle I}$${\textstyle I}$ で添字付けられたベクトル空間の族 ${\textstyle V_{i}}$${\textstyle V_{i}}$の直積 ${\textstyle \prod _{i\in I}V_{i}}$${\textstyle \prod _{i\in I}V_{i}}$とは、順序組 ${\textstyle ({\boldsymbol {v}}_{i})_{i\in I}=({\boldsymbol {v}}_{1},{\boldsymbol {v}}_{2},\dotsc )\quad ({\boldsymbol {v}}_{i}\in V_{i})}$${\textstyle ({\boldsymbol {v}}_{i})_{i\in I}=({\boldsymbol {v}}_{1},{\boldsymbol {v}}_{2},\dotsc )\quad ({\boldsymbol {v}}_{i}\in V_{i})}$全体の成す集合に、加法とスカラー乗法を成分ごとの演算によって定めたものである。この構成の変種として、直和 ${\textstyle \bigoplus _{i\in I}V_{i}}$${\textstyle \bigoplus _{i\in I}V_{i}}$︵あるいは余積 ${\textstyle \coprod _{i\in I}V_{i}}$${\textstyle \coprod _{i\in I}V_{i}}$︶は先の順序組において有限個の例外を除く全ての成分が零ベクトルであるようなものだけを許して得られるものである。添字集合 ${\textstyle I}$${\textstyle I}$が有限ならばこの二つの構成は一致するが、そうでないならば違うものを与える。

テンソル積

詳細は「テンソル積」を参照

同じ体 F上の二つのベクトル空間 Vと Wのテンソル積 (英: tensor product ) V⊗_F Wあるいは単に V⊗ Wは、線型写像を多変数にするような概念の拡張を扱う多重線型代数における中心的な概念のひとつである。写像 g: V× W→ X; (v, w) ↦ g(v, w) が双線型写像であるとは、g が両変数 v, wの何れについても線型であることを言う。これはつまり、w を固定したとき写像 v↦ g(v, w) が線型であり、かつ vを固定した時も同様であることを意味する。

テンソル積は以下のような意味で、双線型写像を普遍的に受け入れる特別のベクトル空間である。それはテンソルと呼ばれる記号の︵形式的な︶有限和

${\boldsymbol {v}}_{1}\otimes {\boldsymbol {w}}_{1}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}_{2}+\dotsb +{\boldsymbol {v}}_{n}\otimes {\boldsymbol {w}}_{n}$${\boldsymbol {v}}_{1}\otimes {\boldsymbol {w}}_{1}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}_{2}+\dotsb +{\boldsymbol {v}}_{n}\otimes {\boldsymbol {w}}_{n}$
の全体からなる線型空間で、これらの元は aをスカラーとして

$a({\boldsymbol {v}}\otimes {\boldsymbol {w}})=(a{\boldsymbol {v}})\otimes {\boldsymbol {w}}={\boldsymbol {v}}\otimes (a{\boldsymbol {w}})$$a({\boldsymbol {v}}\otimes {\boldsymbol {w}})=(a{\boldsymbol {v}})\otimes {\boldsymbol {w}}={\boldsymbol {v}}\otimes (a{\boldsymbol {w}})$
${\boldsymbol {v}}_{1}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}={\boldsymbol {v}}_{1}\otimes {\boldsymbol {w}}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}$${\boldsymbol {v}}_{1}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}={\boldsymbol {v}}_{1}\otimes {\boldsymbol {w}}+{\boldsymbol {v}}_{2}\otimes {\boldsymbol {w}}$
${\boldsymbol {v}}\otimes ({\boldsymbol {w}}_{1}+{\boldsymbol {w}}_{2})={\boldsymbol {v}}\otimes {\boldsymbol {w}}_{1}+{\boldsymbol {v}}\otimes {\boldsymbol {w}}_{2}$${\boldsymbol {v}}\otimes ({\boldsymbol {w}}_{1}+{\boldsymbol {w}}_{2})={\boldsymbol {v}}\otimes {\boldsymbol {w}}_{1}+{\boldsymbol {v}}\otimes {\boldsymbol {w}}_{2}$
なる規則で縛られている。

テンソル積の普遍性を表す可換図式

これらの規則は、写像 f: V× W→ V⊗ W; (v, w) ↦ v⊗ wが双線型となることを保証するものである。テンソル積の普遍性とは

任意のベクトル空間 Xと任意の双線型写像 g: V× W→ Xが与えられたとき、写像 u: V⊗ W→ Xが一意的に存在して、上記の写像 fとの合成 u◦ fが gに等しくなるようにすることができる ( u(v ⊗ w) = g(v, w) )

というものである。テンソル積の普遍性は対象を、その対象からの、あるいはその対象への写像によって間接的に定義するという︵進んだ抽象代数学ではよく用いられる︶手法の一例である。

付加構造を備えたベクトル空間

線型代数学の観点からは、任意のベクトル空間が︵同型を除いて︶その次元によって特徴づけられるという意味で、ベクトル空間については完全に分かっている。しかしベクトル空間というものは﹁本質的に﹂、函数列が別の函数に収束するか否かという︵解析学では重要な︶問題について取り扱う枠組みを提供していないし、同様に加法演算が有限項の和のみを許す線型代数学では無限級数を扱うのには適当でない。従って、函数解析学ではベクトル空間に更なる構造を考える必要が求められる。ほとんど同様に、付加的な情報を持つベクトル空間が有効に働く部分を抽象的に見つけだすことで、公理的取扱いからベクトル空間の持つ代数学的に本質的な特徴を浮き彫りにすることができる。

付加構造の一つの例は、順序集合 ≤ で、これによりベクトルの比較が行えるようになる。例えば、実 n-次元空間 Rⁿは、ベクトルを成分ごとに比較することで順序づけることができる。また、ルベーグ積分は函数を二つの正値函数の差

$f=f^{+}-f^{-}$$f=f^{+}-f^{-}$
として︵f⁺ は fの正部分で f⁻ は負部分︶表すことができることに依拠しているから、順序線型空間︵例えばリース空間︶はルベーグ積分において基本的である。

ノルム空間および内積空間

詳細は「ノルム線型空間」および「計量ベクトル空間」を参照

ベクトルの﹁測度﹂は、ベクトルの長さを測るノルムや、ベクトルの間の角を測る内積を決めることによって与えられる。ノルムが定義されたベクトル空間をノルム空間とよび、ノルムを |v| のように表す。内積が定義されたベクトル空間を内積空間と呼び、 内積は⟨v, w⟩ のように表す。内積空間は付随するノルム

$|{\boldsymbol {v}}|:={\sqrt {\langle {\boldsymbol {v}},{\boldsymbol {v}}\rangle }}$$|{\boldsymbol {v}}|:={\sqrt {\langle {\boldsymbol {v}},{\boldsymbol {v}}\rangle }}$
を持つ。

数ベクトル空間 Fⁿは標準内積

${\boldsymbol {x}}\cdot {\boldsymbol {y}}=x_{1}y_{1}+\dotsb +x_{n}y_{n}$${\boldsymbol {x}}\cdot {\boldsymbol {y}}=x_{1}y_{1}+\dotsb +x_{n}y_{n}$
を備えている。これは R²においてよくある二つのベクトル x, yの成す角 θ の概念を余弦定理

${\boldsymbol {x}}\cdot {\boldsymbol {y}}={\mathopen {|}}{\boldsymbol {x}}{\mathclose {|}}{\mathopen {|}}{\boldsymbol {y}}{\mathclose {|}}\cos(\theta )$${\boldsymbol {x}}\cdot {\boldsymbol {y}}={\mathopen {|}}{\boldsymbol {x}}{\mathclose {|}}{\mathopen {|}}{\boldsymbol {y}}{\mathclose {|}}\cos(\theta )$
によって反映するものである。これにより、x · y= 0 を満たす二つのベクトル x, yは互いに直交すると言われる。この標準内積の重要な変形版として、ミンコフスキー空間 R⁴= R^3,1 はローレンツ積

$\langle {\boldsymbol {x}}\mid {\boldsymbol {y}}\rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}$$\langle {\boldsymbol {x}}\mid {\boldsymbol {y}}\rangle =x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}-x_{4}y_{4}$
を備える。標準内積との大きな違いは、ローレンツ積が正定値でないこと、つまり ⟨x|x⟩ は負の値を取り得る︵例えば x= (0,0,0,1) のとき︶ことである。︵三つの空間的な座標とは異なり、時間に対応する︶第四の座標を考えることは特殊相対性理論の数学的取扱いにおいて有効である。

線型位相空間

詳細は「線型位相空間」を参照

収束性の問題は、ベクトル空間 Vに両立する位相︵近さを記述することを可能にする構造︶を入れることによって扱われる。。 ここでいう﹁両立﹂とは、加法とスカラー乗法がともに連続写像となるという意味で、大雑把に言えば、x, y∈ Vと a∈ Fが限られた範囲の中にあれば、x + yと axも限られた範囲に留まるということである。スカラーについてこの議論がきちんと意味を持つようにするためには、この文脈において体 Fにも位相が定められていなければならない。よく用いられるのが実数体や複素数体である。

このような線型位相空間ではベクトル項級数を考えることができて、V の元からなる列 (f_i)_i ∈ Nの無限和

$\sum _{i=0}^{\infty }f_{i}$$\sum _{i=0}^{\infty }f_{i}$
とは、対応する有限部分和の極限を表すものである。例えば f_iが、ある︵実または複素︶函数空間に属する函数であるとすると、この場合の級数は函数項級数と呼ばれる。函数項級数の収束の様態は、函数空間に課された位相に依存する。そのような様態の中でも各点収束と一様収束の二つは特に際立った例である。

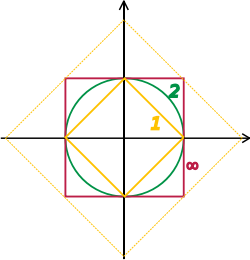
R² の﹁単位球面﹂はノルム 1の平面ベクトルからなる。図は、異なる p-ノルムに関する単位球面を p= 1, 2, ∞ の場合に描いたもの。また大きな菱形は 1-ノルムが √2 に等しいような点を描いたものである。

ある種の無限級数の極限の存在を保証する方法の一つは、考える空間を任意のコーシー列が収束するようなものに限って考えることである。そのようなベクトル空間は完備距離空間であるという。大まかに言えば、ベクトル空間が完備というのは必要な極限をすべて含むということである。例えば単位区間 [0, 1] 上の多項式函数全体の成すベクトル空間に一様収束位相を入れたものは完備でない。これは [0, 1] 上の任意の連続函数が、多項式函数列で一様に近似することができるというストーン＝ワイエルシュトラスの定理による。対照的に、区間 [0, 1] 上の連続函数全体の成す空間に同じ位相を入れたものは完備になる。ノルムからは、ベクトル列 v_nが vに収束する必要十分条件を

$\lim _{n\to \infty }|{\boldsymbol {v}}_{n}-{\boldsymbol {v}}|=0$$\lim _{n\to \infty }|{\boldsymbol {v}}_{n}-{\boldsymbol {v}}|=0$
で定めることによって、空間に位相が入る。バナッハ空間およびヒルベルト空間は、それぞれノルムおよび内積から定まる位相に関して完備な位相空間である。函数解析学で重要になるそれらの研究は、有限次元位相線型空間上のノルムはどれも同じ収束性の概念を定めるから、無限次元ベクトル空間に焦点があてられる。図は R²上の 1ノルムと ∞ ノルムとの同値性を示すものである。単位﹁球体﹂は互いに他に囲まれているから、列が 1ノルムに関して 0 に収束することと、その列が ∞ ノルムに関して収束することとが同値になる。しかし無限次元空間の場合には、一般には互いに同値でないような位相が存在しおり、そのことが位相線型空間の研究を、付加構造を持たない純代数的なベクトル空間の理論よりも豊かなものとしているのである。

概念的な観点では、位相線型空間に関する全ての概念は位相とうまく合うものでなければならない。例えば、位相線型空間の間の線型写像︵あるいは線型汎函数︶V → Wは連続であるものと仮定される。特に、︵位相的︶双対空間 V^∗ は連続汎函数 V→ R(orC) からなるものとする。基礎を成すハーン-バナッハの定理は、適当な位相線型空間を連続汎函数によって部分空間に分けることに関係するものである。

バナッハ空間

詳細は「バナッハ空間」を参照

ステファン・バナフの導入したバナッハ空間とは、完備ノルム空間のことである。一つの例として、$\ell ^{p}$$\ell ^{p}$ (1 ≤ p≤ ∞) は、実数を成分とする無限次元ベクトル x= (x₁, x₂, ...) であって、p < ∞ に対して

$|{\boldsymbol {x}}|_{p}:={\biggl (}\sum _{i}|x_{i}|^{p}{\biggr )}^{1/p}$$|{\boldsymbol {x}}|_{p}:={\biggl (}\sum _{i}|x_{i}|^{p}{\biggr )}^{1/p}$
または p= ∞ に対して

$|{\boldsymbol {x}}|_{\infty }:=\sup _{i}|x_{i}|$$|{\boldsymbol {x}}|_{\infty }:=\sup _{i}|x_{i}|$
で定義される p-ノルムが有限となるようなもの全体の成すベクトル空間である。無限次元空間 $\ell ^{p}$$\ell ^{p}$の位相は、異なる pに対しては同値でない。例えばベクトルの列 x_n= (2⁻ⁿ, 2⁻ⁿ, ..., 2⁻ⁿ, 0, 0, ...), つまり各項が最初の 2ⁿ-個の成分が 2⁻ⁿ で残りはすべて 0 となるような無限次元ベクトルとなるようなベクトル列は p= ∞ のときは零ベクトルに収束するが、p = 1 のときはそうならない。式にすれば

$|x_{n}|_{\infty }=\sup(2^{-n},0)=2^{-n}\to 0$$|x_{n}|_{\infty }=\sup(2^{-n},0)=2^{-n}\to 0$
だが

$|x_{n}|_{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1$$|x_{n}|_{1}=\sum _{i=1}^{2^{n}}2^{-n}=2^{n}\cdot 2^{-n}=1$
である。

実数列よりも一般の函数 f : Ω → Rは、上記の和のところをルベーグ積分に置き換えた

${\displaystyle |f|_{p}:=\left(\int _{\Omega }{\bigl |}f($x){\bigr |}^{p}\,dx\right)^{1/p}} $|f|_{p}:=\left(\int _{\Omega }{\bigl |}f(x){\bigr |}^{p}\,dx\right)^{1/p}$
をノルムとして備えている。与えられた領域 Ω︵例えば区間︶上の |f|^p < ∞ を満足する可積分函数の空間に、このノルムを入れたものはルベーグ空間 L^p(Ω) と呼ばれる。ルベーグ空間は何れも完備になる︵が、もし上記の積分をリーマン積分としたならば、空間は完備にならない。これがルベーグ積分論を考えることの正当性の一つとして挙げられる理由の一つである︶。具体的に書けば、任意の可積分函数列 f₁, f₂, ... で  |f_n|_p < ∞ となるものが、条件

${\displaystyle \lim _{k,\ n\to \infty }\int _{\Omega }{\bigl |}f_{k}($x)-f_{n}(x){\bigr |}^{p}\,dx=0} $\lim _{k,\ n\to \infty }\int _{\Omega }{\bigl |}f_{k}(x)-f_{n}(x){\bigr |}^{p}\,dx=0$
を満足するならば、適当な函数 f(x) でベクトル空間 L^p(Ω) に属するものが存在して

${\displaystyle \lim _{k\to \infty }\int _{\Omega }{\bigl |}f($x)-f_{k}(x){\bigr |}^{p}\,dx=0} $\lim _{k\to \infty }\int _{\Omega }{\bigl |}f(x)-f_{k}(x){\bigr |}^{p}\,dx=0$
を満たすようにすることができる。

函数自体だけでなくその導函数にも有界性条件を課すことでソボレフ空間の概念が導かれる。

ヒルベルト空間

詳細は「ヒルベルト空間」を参照

正弦函数 (赤) の有限和によって、周期函数 (青) を近似する様子を、初項から 5-項までの和を順に示すことによって示したもの。

完備な内積空間はダフィット・ヒルベルトに因んでヒルベルト空間 (英: Hilbert space) と呼ばれる。自乗可積分函数の空間 L²(Ω) に

${\displaystyle \langle f,g\rangle =\int _{\Omega }f($x){\overline {g(x)}}\,dx} $\langle f,g\rangle =\int _{\Omega }f(x){\overline {g(x)}}\,dx$
で定義される内積︵ただし g(x) は g(x) の複素共役とする︶を入れたものは主要なヒルベルト空間の例である。

定義によりヒルベルト空間における任意のコーシー列は極限を持つから、逆に与えられた極限函数を近似するという適当な性質を持つ函数列 f_nを求めることが重要になる。初期の解析学では、テイラー近似の形で可微分函数 fの多項式列による近似が確立された。ストーン＝ヴァイアシュトラスの定理により、[a, b] 上の任意の連続函数は適当な多項式列によりいくらでも近く近似できる。三角関数を用いた同様の近似法は一般にフーリエ展開と呼ばれ、工学において広く応用される︵#フーリエ変換節を参照︶。より一般に、またより概念的に言えば、これらの定理は﹁基本函数族﹂とは何であるかということを端的に記述するものになっている。あるいは抽象ヒルベルト空間においてどのような基本ベクトル族が、ヒルベルト空間 Hを位相的に生成するに十分であるかをいうものである。ここで、位相的に生成する︵あるいは単に生成する︶とは、それらの位相的線型包と呼ばれる、線型包の閉包︵即ち、有限線型結合およびその極限︶が、全体空間に一致することである。そのような函数の集合は Hの基底︵あるいはヒルベルト基底︶と呼ばれ、基底の濃度はヒルベルト空間 Hのヒルベルト次元と呼ばれる。これらの定理は適当な基底函数族が近似の目的で十分性を示すことのみならず、グラム・シュミットの正規直交化法を用いて正規直交基底が得られることも意味している。そのような直交基底は、有限次元ユークリッド空間における座標軸をヒルベルト空間に対して一般化したものと考えることができる。 

様々な微分方程式に対して、その解をヒルベルト空間の言葉で解釈することができる。例えば物理学や工学におけるかなり多くの分野でそのような方程式が導かれ、特定の物理的性質を持つ解が︵しばしば直交する︶基底函数族としてよく扱われる。物理学からの例として、量子力学における時間依存シュレーディンガー方程式は、その解が波動関数と呼ばれる偏微分方程式として、物理的性質の時間的な変化を記述する。。エネルギーやモーメントのような物理的性質に対する明確な値は、ある種の線型微分作用素の固有値とそれに属する固有状態と呼ばれる波動函数に対応する。スペクトル定理は、函数に作用する線型コンパクト作用素を、それらの固有値と固有函数を用いて分解することを述べるものである。

体上の多元環

詳細は「体上の多元環」および「リー環」を参照

方程式 xy = 1 で与えられる双曲線。この双曲線上の函数の座標環は R[x, y] / (xy − 1) で与えられ、R 上無限次元のベクトル空間になる。

一般のベクトル空間は、ベクトルの間の乗法を持たない。二つのベクトルの乗法を定める双線型写像を付加的に備えたベクトル空間は、体上の多元環と言う。主な多元環は、何らかの幾何学的な対象の上の函数の空間から生じる。体に値をとる函数は、点ごとの乗法を持ち、それら函数の全体が多元環を成すのである。例えば、ストーン＝ヴァイアシュトラスの定理は、バナッハ空間にも多元環にもなっているバナッハ環において成立する。

可換多元環は一変数または多変数の多項式環を使ってたくさん作れる。可換多元環の乗法は可換かつ結合的である。これらの環およびその剰余環は、それが代数幾何的対象上の函数の環となることから、代数幾何学の基礎を成している。

別の重要な例はリー環である。リー環の乗法︵x, yの積を [x, y] と書く︶は可換でも結合的でもないが、そうなることは制約条件

●反対称性: [x, y] = −[y, x]

●ヤコビの等式: [x, [y, z]] + [y, [z, x]] + [z, [x, y]] = 0

によって制限されている。リー環の例には、n-次正方行列全体の成すベクトル空間に、行列の交換子  [x, y] = xy− yxを積としたものや、R³ にクロス積を入れたものなどが含まれる。

テンソル代数 T(V) は任意のベクトル空間に積を導入して多元環を得るための形式的な方法である。T(V) はベクトル空間としては、単純テンソルあるいは分解可能型テンソルと呼ばれる記号

${\boldsymbol {v}}_{1}\otimes {\boldsymbol {v}}_{2}\otimes \dotsb \otimes {\boldsymbol {v}}_{n}$${\boldsymbol {v}}_{1}\otimes {\boldsymbol {v}}_{2}\otimes \dotsb \otimes {\boldsymbol {v}}_{n}$
によって生成される︵ただし、テンソルの階数 nは任意に動かすものとする︶。乗法は二つのベクトル空間に対してテンソル積を定義するときとほとんど同じで、基底元についてはそれらの記号をテンソル積 ⊗ で結合することで与え、一般には加法に対する分配法則を以って基底元に対する積を延長する。スカラー倍の積は ⊗ と可換であるものとする。こうして得られる T(V) においては、一般に v₁⊗ v₂と v₂⊗ v₁との間には何の関係も成立しない。この二つの元を強制的に等しいものと定めると対称代数 S(V) が、あるいは強制的に  v₁⊗ v₂= − v₂⊗ v₁と置けば外積代数 ${\textstyle \bigwedge ($V)} ${\textstyle \bigwedge (V)}$がそれぞれ得られる。

基礎とする体 Fを明示したい場合には、F-多元環あるいは F-代数という言葉がよく用いられる。

応用

ベクトル空間の多様体に対する応用は様々な状況で生じてくる。つまり多様体上で定義され、ある体に値をとる函数を考えれば、そこにはベクトル空間が生じるのである。そのようなベクトル空間を考えれば、解析学や幾何学における問題を取り扱う枠組みが提供される。またそういったベクトル空間はフーリエ変換などにおいても利用される。ここで挙げた例は網羅的なものではなく、例えば数理最適化など、ほかにももっと多くの応用が存在する。ゲーム理論のミニマックス法は全てのプレイヤーが最適な試行を行うことができるならば一意的なペイが得られることを述べるもので、これはベクトル空間法を用いて証明できる。表現論は、よく分かっている線型代数学およびベクトル空間に関する内容を、群論など他の領域に実り豊かに引き写すものである。

シュワァルツ超函数

詳細は「シュワルツ超函数」を参照

シュヴァルツ超函数 (英: distribution) は、各﹁試験﹂函数︵典型的には、関数の台を持つ滑らかな関数︶に数を連続的な仕方で割り当てる線型写像をいう。即ち、シュヴァルツ超函数の空間は、試験函数の空間の︵連続的︶双対である。後者の空間には、試験函数 fそれ自体のみならずその高階導函数までを考慮するような位相が入っている。シュヴァルツ超函数の典型的な例はある領域 Ω 上で試験函数 fを積分する作用素

${\displaystyle I($f)=\int _{\Omega }f(x)\,dx} $I(f)=\int _{\Omega }f(x)\,dx$
である。Ω が一点集合{p}のとき、これは試験函数 fに点 pにおける値を割り当てるディラックのデルタ関数 δ を定める︵δ(f) = f(p)︶。

シュヴァルツ超函数は微分方程式を解くための強力な道具である。微分は線型であるといったような、解析学の標準的な概念は、自然にシュヴァルツ超函数の空間へ延長することができるから、従って問題の方程式をシュヴァルツ超函数の空間へ引き写すことができて、しかもシュヴァルツ超函数の空間はもとの函数空間よりも大きいから、方程式を解くためにより柔軟な方法が利用できる︵例えば、グリーン関数法︶。

また、基本解は真の函数でなくシュヴァルツ超函数解︵弱解︶となるのがふつうであり、弱解から所期の境界条件を満たす方程式の真の解を求めるには、見つかった弱解が実際に真の函数となることを確かめればよく、証明できた場合にはそれがもとの方程式の真の解である︵例えばリースの表現定理の帰結である弱形式が利用できる︶。

フーリエ変換

詳細は「フーリエ変換」を参照

熱方程式は、冷たい環境におかれた熱源の温度の低下のような、時間とともに散逸する物理的性質を記述したものである。（黄色は赤よりも冷たい領域を表す）

周期関数をフーリエ級数を成す三角関数の和に分解することは物理学や工学においてよく用いられる手法である。台となるベクトル空間は、ふつうはヒルベルト空間 L²(0, 2π) であり、函数族 sin mxおよび cos mx(m は整数) が正規直交基底を与える。L²-函数 fのフーリエ展開は

${\displaystyle {\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }{\bigl [}a_{m}\cos($mx)+b_{m}\sin(mx){\bigr ]}} ${\frac {a_{0}}{2}}+\sum _{m=1}^{\infty }{\bigl [}a_{m}\cos(mx)+b_{m}\sin(mx){\bigr ]}$
である。係数 a_m, b_m は fのフーリエ係数と呼ばれ、公式

${\displaystyle a_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f($t)\cos(mt)dt,\quad b_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\sin(mt)dt} $a_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\cos(mt)dt,\quad b_{m}={\frac {1}{\pi }}\int _{0}^{2\pi }f(t)\sin(mt)dt$
で求められる。

物理学の言葉で言えば、函数は正弦波の重ね合せとして表され、その係数は函数の周波数スペクトルについての情報を与えるということになる。複素型のフーリエ級数も広く用いられる。 上記の具体的な公式は、より一般のポントリャーギン双対と呼ばれる双対からの帰結である。加法群 Rにこの双対性を適用すれば古典的なフーリエ変換が得られる。また物理学では逆格子に応用される。これは有限次元実線型空間に付加的なデータとして原子や結晶の位置を符号化した束を与えたものを基礎の群として双対性を適用したものである。

フーリエ級数は偏微分方程式の境界値問題を解くのにも利用される。1822年にジョゼフ・フーリエが初めてこの方法を熱方程式を解くために用いた。フーリエ級数の離散版は標本化において、函数値が等間隔に並んだ有限個の点でしかわかっていないところで用いられる。この場合、フーリエ級数は有限項で、その値は全ての点で標本値に等しい。また、係数全体の成す集合は、与えられた標本列の離散フーリエ変換 (英: DFT : Discrete Fourier Transformation) と呼ばれる。この DFT は︵レーダーや音声符号化や画像圧縮などに応用を持つ︶デジタル信号処理の重要な道具の一つである。画像フォーマットJPEGは、近しい関係にある離散コサイン変換の応用である。

高速フーリエ変換は離散フーリエ変換を高速に計算するアルゴリズムである。これはフーリエ係数の計算だけでなく、畳み込みを用いて、二つの有限列の畳み込みを計算するのにも利用できる。また、ディジタルフィルタや、巨大な整数や多項式の高速な掛け算アルゴリズム︵ショーンハーゲ・ストラッセン法︶にも応用できる。

微分幾何学

詳細は「接ベクトル空間」を参照

二次元球面のある点における接空間とは、この点で球面に接する無限平面である。

曲面のある点における接平面は、自然に接点を原点と同一視したベクトル空間になる。接平面は接点における曲面の最適線型近似あるいは線型性である。三次元ユークリッド空間の場合でさえ、接平面の基底を指定する自然な方法は点綴的には存在せず、またそれゆえに接平面は、実数ベクトル空間というよりはむしろ抽象ベクトル空間として考えられる。接空間はより高次元の可微分多様体への一般化である。

リーマン多様体はその接空間が適当な内積を備えた多様体である。そこから得られるリーマン曲率テンソルは、それ一つでその多様体の全ての曲率を表すことができるもので、一般相対性理論では例えば時空の質量とエネルギー定数を記述するアインシュタインテンソルなどに応用がある。リー群の接空間は自然にリー環の構造を持ち、コンパクト群の分類に用いることができる。

一般化

ベクトル束

詳細は「ベクトル束」および「接束」を参照

メビウスの帯。これは局所的には U × R に同相である。

ベクトル束は位相空間 Xによって連続的に径数付けられたベクトル空間の族である。より明確に言えば、X 上のベクトル束とは、位相空間 Eであって、連続写像

$\pi \colon E\to X$$\pi \colon E\to X$
を持ち、X の各点 xにおいてファイバー V= π⁻¹(x) がベクトル空間を成すようなものを言う。dim V= 1 ならば直線束という。任意のベクトル空間 Vに対し、射影 X× V→ Xは直積 X× Vをファイバー束にする。X 上のベクトル束は、局所性のある︵固定された︶ベクトル空間 Vと Xとの直積でなければならない。つまり、X の各点 xに対して xの適当な近傍 Uを選んで、π の π⁻¹(U) への制限が自明束 U× V→ Uに同型となるようにすることができる。これらの局所自明性にもかかわらず、ベクトル束は巨視的には︵台となる位相空間 Xの形に依存して︶﹁捻じれ﹂ているのである。つまり、ベクトル束は自明束 X× V︵と大域的に同型︶である必要はない。例えば、メビウスの帯は︵円周を実数直線上の半開区間と同一視することによって︶円周 S¹上の線束と見做すことができるが、しかしこれは円筒 S¹× Rとは異なる。後者は向き付け可能性だが、前者はそうではない。

ある種のベクトル束の性質は、台となる位相空間についての情報を提供する。例えば、接空間の集まりからなる接束は可微分多様体の点によって径数付けられる。円周 S¹の接束は、S¹ 上に大域的な非零ベクトル場が存在するから、大域的に S¹× Rに同型である。対照的に、毛玉の定理により、二次元球面 S²上の接ベクトル場で至る所消えていない者は存在しない。K-理論は同じ位相空間上の全てのベクトル束の同型類について研究するものである。深い位相的かつ幾何学的な観察に加えて、この理論には実有限次元多元体の分類︵そのようなものは R, Cのほかは四元数体 Hと八元数体 Oしかない︶というような純代数学的な帰結も存在する︵フルヴィッツの定理を参照︶。

可微分多様多の余接束は、多様体の各点において接空間の双対である余接空間が対応するベクトル束である。余接束の切断は1-形式 (1-form) と呼ばれる。

加群

詳細は「環上の加群」を参照

ベクトル空間が体に対するものであるように、加群 (英: modules) の概念は環に対するものである。これはベクトル空間の公理において体 Fとするところを環 Rで置き換えることで得られる。加群の理論はベクトル空間のそれと比べて︵環の元に必ずしも逆元が存在しないことで︶より複雑なものになっている。例えば加群は、Z-加群︵つまりアーベル群︶としての Z/2Z のように、必ずしも基底を持たない。基底を持つような加群︵ベクトル空間もそう︶は自由加群と呼ばれる。にも拘わらずベクトル空間は、係数環が体であるような加群として簡単に定義することができて、その元をベクトルと呼ぶ。可換環の代数幾何学的解釈は、それらの環のスペクトルを通じて、ベクトル束の代数的な対応物である局所自由加群の概念などを展開することを可能にする。

アフィン空間および射影空間

詳細は「アフィン空間」および「射影空間」を参照

R³ 内のアフィン平面 (水色): これは二次元の線型部分空間をベクトル x (赤) でずらしたものである。

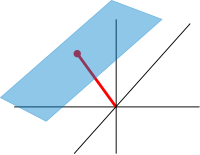
大雑把に言うと、アフィン空間 (英: affine space ) というのはベクトル空間からその原点をわからなくしたものである。より正確には、アフィン空間とは自由かつ推移的なベクトル空間の群作用を備えた集合を言う。特にベクトル空間は、写像

$V\times V\to V;({\boldsymbol {v}},{\boldsymbol {a}})\mapsto {\boldsymbol {a}}+{\boldsymbol {v}}$$V\times V\to V;({\boldsymbol {v}},{\boldsymbol {a}})\mapsto {\boldsymbol {a}}+{\boldsymbol {v}}$
を考えることによって、自身の上のアフィン空間となる。W をベクトル空間とするとき、W のアフィン部分空間とは、固定したベクトル x∈ Wによって線型部分空間 Vを平行移動することによって得られるものを言う。この空間は x+ V︵V による Wの剰余類︶であり、v ∈ Vに対する x+ vの形のベクトル全てからなる。重要な例は、非斉次の線型方程式系

$A{\boldsymbol {x}}={\boldsymbol {b}}$$A{\boldsymbol {x}}={\boldsymbol {b}}$
の解空間である。これは斉次の場合、つまり  b= 0 の場合を一般化するものである。この解空間は、方程式の特殊解 xと、付随する斉次方程式の解空間︵つまり Aの核空間︶V に対するアフィン部分空間 x+ Vである。

固定された有限次元ベクトル空間 Vの一次元線型部分空間全体の成す集合は射影空間と呼ばれる。これは平行線が無限遠において交わるという概念の定式化に用いられる。グラスマン多様体および旗多様体はそれぞれ、決まった次元 kの線型部分空間および旗と呼ばれる線型部分空間の包含列を径数付けることによる、射影空間の概念の一般化である。

凸解析

詳細は「凸解析」を参照

n-次元単体は標準凸集合で、任意の多面体へ写り、また、標準 (n + 1)-次元アフィン超平面（標準アフィン空間）と標準 (n + 1)-次元象限（標準錐体）との交わりになっている。

順序体︵特に実数体︶上で、凸解析の概念を考えることができる。最も基本的なものは、非負線型結合全体からなる錐、および和が 1となる非負線型結合全体からなる凸集合である。凸集合はアフィン空間の公理と錐体の公理を組み合わせたものとして見ることができ、これは凸集合の標準空間である n-単体が超平面と象限との交わりであることを反映したものになっている。このような空間は特に線型計画問題において用いられる。

普遍代数学の言葉で言えば、ベクトル空間はベクトルの有限和に対応する係数の有限列全体の成す普遍ベクトル空間 K^∞ 上の代数であるが、一方アフィン空間はここでいう︵和が 1の有限列全体の成す︶普遍アフィン超平面上の代数であり、また錐体は普遍象限上の代数、凸集合は普遍単体上の代数である。これは、﹁座標に対する︵可能な︶制限和﹂を用いて公理を幾何化したものである。

線型代数学における多くの概念は凸解析における対応する概念があって、基本的なものとしては基底や︵凸包のような形での︶生成概念など、また重要なものとしては︵双対多角形、双対錐と極錐、双対問題のような︶双対性などが含まれる。しかし線型代数学において任意のベクトル空間やアフィン空間が標準空間に同型となるのとは異なり、任意の凸集合や錐体が単体や象限に同型となるわけではない。むしろ単体から多面体の上への写像が一般化された重心座標系によって常に存在し、またその双対写像として多面体から︵面の数と等しい次元の︶象限の中への写像がスラック変数によって存在するが、これらが同型となることは稀である︵ほとんどの多面体は単体でも象限でもない︶。

参考文献

線型代数学に関するもの

• Artin, Michael (1991), Algebra, Prentice Hall, ISBN 978-0-89871-510-1 
• Blass, Andreas (1984), “Existence of bases implies the axiom of choice”, Axiomatic set theory, Contemporary Mathematics, 31, Providence, RI: American Mathematical Society, pp. 31–33, doi:10.1090/conm/031, ISBN 0-8218-5026-1, MR763890, http://www.math.lsa.umich.edu/~ablass/bases-AC.pdf 
• Brown, William A. (1991), Matrices and vector spaces, New York: M. Dekker, ISBN 978-0-8247-8419-5 
• Lang, Serge (1987), Linear algebra, Berlin, New York: Springer-Verlag, ISBN 978-0-387-96412-6 
• Lang, Serge (2002), Algebra, Graduate Texts in Mathematics, 211 (Revised third ed.), New York: Springer-Verlag, ISBN 978-0-387-95385-4, MR1878556, https://books.google.co.jp/books?id=Fge-BwqhqIYC 
• Mac Lane, Saunders (1999), Algebra (3rd ed.), pp. 193–222, ISBN 0-8218-1646-2 
• Meyer, Carl D. (2000), Matrix Analysis and Applied Linear Algebra, SIAM, ISBN 978-0-89871-454-8, http://www.matrixanalysis.com/ 
• Roman, Steven (2005), Advanced Linear Algebra, Graduate Texts in Mathematics, 135 (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-24766-3 
• Spindler, Karlheinz (1993), Abstract Algebra with Applications: Volume 1: Vector spaces and groups, CRC, ISBN 978-0-8247-9144-5 
• （ドイツ語） van der Waerden, Bartel Leendert (1993), Algebra (9th ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-56799-8 

解析学に関するもの

• Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-13627-9 
• Bourbaki, Nicolas (2004), Integration I, Berlin, New York: Springer-Verlag, ISBN 978-3-540-41129-1 
• Braun, Martin (1993), Differential equations and their applications: an introduction to applied mathematics, Berlin, New York: Springer-Verlag, ISBN 978-0-387-97894-9 
• BSE-3 (2001), “Tangent plane”, in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4, https://www.encyclopediaofmath.org/index.php?title=Tangent_plane 
• Choquet, Gustave (1966), Topology, Boston, MA: Academic Press 
• Dennery, Philippe; Krzywicki, Andre (1996), Mathematics for Physicists, Courier Dover Publications, ISBN 978-0-486-69193-0 
• Dudley, Richard M. (1989), Real analysis and probability, The Wadsworth & Brooks/Cole Mathematics Series, Pacific Grove, CA: Wadsworth & Brooks/Cole Advanced Books & Software, ISBN 978-0-534-10050-6 
• Dunham, William (2005), The Calculus Gallery, Princeton University Press, ISBN 978-0-691-09565-3 
• Evans, Lawrence C. (1998), Partial differential equations, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0772-9 
• Folland, Gerald B. (1992), Fourier Analysis and Its Applications, Brooks-Cole, ISBN 978-0-534-17094-3 
• Gasquet, Claude; Witomski, Patrick (1999), Fourier Analysis and Applications: Filtering, Numerical Computation, Wavelets, Texts in Applied Mathematics, New York: Springer-Verlag, ISBN 0-387-98485-2 
• Ifeachor, Emmanuel C.; Jervis, Barrie W. (2001), Digital Signal Processing: A Practical Approach (2nd ed.), Harlow, Essex, England: Prentice-Hall (2002発行), ISBN 0-201-59619-9 
• Krantz, Steven G. (1999), A Panorama of Harmonic Analysis, Carus Mathematical Monographs, Washington, DC: Mathematical Association of America, ISBN 0-88385-031-1 
• Kreyszig, Erwin (1988), Advanced Engineering Mathematics (6th ed.), New York: John Wiley & Sons, ISBN 0-471-85824-2 
• Kreyszig, Erwin (1989), Introductory functional analysis with applications, Wiley Classics Library, New York: John Wiley & Sons, ISBN 978-0-471-50459-7, MR992618 
• Lang, Serge (1983), Real analysis, Addison-Wesley, ISBN 978-0-201-14179-5 
• Lang, Serge (1993), Real and functional analysis, Berlin, New York: Springer-Verlag, ISBN 978-0-387-94001-4 
• Loomis, Lynn H. (1953), An introduction to abstract harmonic analysis, Toronto-New York–London: D. Van Nostrand Company, Inc., pp. x+190 
• Schaefer, Helmut H.; Wolff, M.P. (1999), Topological vector spaces (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98726-2 
• Treves, François (1967), Topological vector spaces, distributions and kernels, Boston, MA: Academic Press 

歴史に関するもの

• （フランス語） Banach, Stefan (1922), “Sur les opérations dans les ensembles abstraits et leur application aux équations intégrales (On operations in abstract sets and their application to integral equations)”, Fundamenta Mathematicae 3, ISSN 0016-2736, http://matwbn.icm.edu.pl/ksiazki/fm/fm3/fm3120.pdf 
• （ドイツ語） Bolzano, Bernard (1804), Betrachtungen über einige Gegenstände der Elementargeometrie (Considerations of some aspects of elementary geometry), http://dml.cz/handle/10338.dmlcz/400338 
• （フランス語） Bourbaki, Nicolas (1969), Éléments d'histoire des mathématiques (Elements of history of mathematics), Paris: Hermann 
• Dorier, Jean-Luc (1995), “A general outline of the genesis of vector space theory”, Historia Mathematica 22 (3): 227–261, doi:10.1006/hmat.1995.1024, MR1347828, http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6WG9-45NJHDR-C&_user=1634520&_coverDate=12%2F31%2F1995&_rdoc=2&_fmt=high&_orig=browse&_srch=doc-info(%23toc%236817%231995%23999779996%23308480%23FLP%23display%23Volume)&_cdi=6817&_sort=d&_docanchor=&_ct=9&_acct=C000054038&_version=1&_urlVersion=0&_userid=1634520&md5=fd995fe2dd19abde0c081f1e989af006 
• （フランス語） Fourier, Jean Baptiste Joseph (1822), Théorie analytique de la chaleur, Chez Firmin Didot, père et fils, https://books.google.co.jp/books?id=TDQJAAAAIAAJ&redir_esc=y&hl=ja 
• （ドイツ語） Grassmann, Hermann (1844), Die Lineale Ausdehnungslehre - Ein neuer Zweig der Mathematik, O. Wigand, https://books.google.co.jp/books?id=bKgAAAAAMAAJ&pg=PA1&dq=Die+Lineale+Ausdehnungslehre+ein+neuer+Zweig+der+Mathematik&redir_esc=y&hl=ja , reprint: Grassmann, Hermann (2000), Kannenberg, L.C., ed., Extension Theory, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2031-5 
• Hamilton, William Rowan (1853), Lectures on Quaternions, Royal Irish Academy, http://historical.library.cornell.edu/cgi-bin/cul.math/docviewer?did=05230001&seq=9 
• （ドイツ語） Möbius, August Ferdinand (1827), Der Barycentrische Calcul : ein neues Hülfsmittel zur analytischen Behandlung der Geometrie (Barycentric calculus: a new utility for an analytic treatment of geometry), http://mathdoc.emath.fr/cgi-bin/oeitem?id=OE_MOBIUS__1_1_0 
• Moore, Gregory H. (1995), “The axiomatization of linear algebra: 1875–1940”, Historia Mathematica 22 (3): 262–303, doi:10.1006/hmat.1995.1025, http://www.sciencedirect.com/science?_ob=ArticleURL&_udi=B6WG9-45NJHDR-D&_user=1634520&_coverDate=12%2F31%2F1995&_rdoc=3&_fmt=high&_orig=browse&_srch=doc-info(%23toc%236817%231995%23999779996%23308480%23FLP%23display%23Volume)&_cdi=6817&_sort=d&_docanchor=&_ct=9&_acct=C000054038&_version=1&_urlVersion=0&_userid=1634520&md5=4327258ef37b4c293b560238058e21ad 
• （イタリア語） Peano, Giuseppe (1888), Calcolo Geometrico secondo l'Ausdehnungslehre di H. Grassmann preceduto dalle Operazioni della Logica Deduttiva, Turin 

発展的話題に関するもの

• Ashcroft, Neil; Mermin, N. David (1976), Solid State Physics, Toronto: Thomson Learning, ISBN 978-0-03-083993-1 
• Atiyah, Michael Francis (1989), K-theory, Advanced Book Classics (2nd ed.), Addison-Wesley, ISBN 978-0-201-09394-0, MR1043170 
• Bourbaki, Nicolas (1998), Elements of Mathematics : Algebra I Chapters 1-3, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64243-5 
• Bourbaki, Nicolas (1989), General Topology. Chapters 1-4, Berlin, New York: Springer-Verlag, ISBN 978-3-540-64241-1 
• Coxeter, Harold Scott MacDonald (1987), Projective Geometry (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-96532-1 
• Eisenberg, Murray; Guy, Robert (1979), “A proof of the hairy ball theorem”, The American Mathematical Monthly (Mathematical Association of America) 86 (7): 572–574, doi:10.2307/2320587, JSTOR 2320587, https://jstor.org/stable/2320587 
• Eisenbud, David (1995), Commutative algebra, Graduate Texts in Mathematics, 150, Berlin, New York: Springer-Verlag, MR1322960, ISBN 978-0-387-94268-1, 978-0-387-94269-8 
• Goldrei, Derek (1996), Classic Set Theory: A guided independent study (1st ed.), London: Chapman and Hall, ISBN 0-412-60610-0 
• Griffiths, David J. (1995), Introduction to Quantum Mechanics, Upper Saddle River, NJ: Prentice Hall, ISBN 0-13-124405-1 
• Halmos, Paul R. (1974), Finite-dimensional vector spaces, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90093-3 
• Halpern, James D. (Jun 1966), “Bases in Vector Spaces and the Axiom of Choice”, Proceedings of the American Mathematical Society (American Mathematical Society) 17 (3): 670–673, doi:10.2307/2035388, JSTOR 2035388, https://jstor.org/stable/2035388 
• Husemoller, Dale (1994), Fibre Bundles (3rd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-94087-8 
• Jost, Jürgen (2005), Riemannian Geometry and Geometric Analysis (4th ed.), Berlin, New York: Springer-Verlag, ISBN 978-3-540-25907-7 
• Kreyszig, Erwin (1991), Differential geometry, New York: Dover Publications, pp. xiv+352, ISBN 978-0-486-66721-8 
• Kreyszig, Erwin (1999), Advanced Engineering Mathematics (8th ed.), New York: John Wiley & Sons, ISBN 0-471-15496-2 
• Luenberger, David (1997), Optimization by vector space methods, New York: John Wiley & Sons, ISBN 978-0-471-18117-0 
• Mac Lane, Saunders (1998), Categories for the Working Mathematician (2nd ed.), Berlin, New York: Springer-Verlag, ISBN 978-0-387-98403-2 
• Misner, Charles W.; Thorne, Kip; Wheeler, John Archibald (1973), Gravitation, W. H. Freeman, ISBN 978-0-7167-0344-0 
• Naber, Gregory L. (2003), The geometry of Minkowski spacetime, New York: Dover Publications, ISBN 978-0-486-43235-9, MR2044239 
• （ドイツ語） Schönhage, A.; Strassen, Volker (1971), “Schnelle Multiplikation großer Zahlen (Fast multiplication of big numbers)”, Computing 7: 281–292, ISSN 0010-485X, http://www.springerlink.com/content/y251407745475773/fulltext.pdf 
• Spivak, Michael (1999), A Comprehensive Introduction to Differential Geometry (Volume Two), Houston, TX: Publish or Perish 
• Stewart, Ian (1975), Galois Theory, Chapman and Hall Mathematics Series, London: Chapman and Hall, ISBN 0-412-10800-3 
• Varadarajan, V. S. (1974), Lie groups, Lie algebras, and their representations, Prentice Hall, ISBN 978-0-13-535732-3 
• Wallace, G.K. (Feb 1992), “The JPEG still picture compression standard”, IEEE Transactions on Consumer Electronics 38 (1): xviii–xxxiv, ISSN 0098-3063 
• Weibel, Charles A. (1994), An introduction to homological algebra, Cambridge Studies in Advanced Mathematics, 38, Cambridge University Press, ISBN 978-0-521-55987-4, OCLC 36131259, MR1269324 

関連項目

• 線型代数学
• 直交座標系
• 空間ベクトル - 物理学におけるベクトル
• 次数付きベクトル空間
• 距離空間
• p-ベクトル（外積代数の元）
• リース＝フィッシャーの定理
• 空間 (数学)

外部リンク

• 『ベクトル空間』 - コトバンク
• Weisstein, Eric W. "Vector Space". mathworld.wolfram.com (英語).
• vector space - PlanetMath.（英語）
• A lecture about fundamental concepts related to vector spaces (given at MIT)
• A graphical simulator for the concepts of span, linear dependency, base and dimension