四元数
i²=j²=k²=−1と(ij,jk,ki)=(−ji,−kj,−ik)=(k,i,j)で定義される複素数の非可換拡張
(クォータニオンから転送)
| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
数学における四元数︵しげんすう、英: quaternion︶とは、複素数を拡張した数体系であり、虚数単位 i, j, kを用いて
a + bi+ cj+ dk
と表せる数のことである。ここで、a, b, c, dは実数であり、虚数単位 i, j, kは以下の関係を満たす。
 このとき 1, i, j, kは実数体上線型独立である。
四元数は純粋数学のみならず応用数学、特に3Dグラフィクスやコンピュータビジョンにおいて三次元での回転の計算でも用いられる。これはオイラー角や回転行列あるいはそれらに代わる道具などとともに、必要に応じて利用される。
四元数についての最初の記述は、1843年にアイルランドの数学者ウィリアム・ローワン・ハミルトンによってなされ[1][2]、3次元空間の力学に応用された。
四元数の特徴は、積について非可換であることである。ハミルトンは、四元数を三次元空間内の二つの有向直線の商として定義した[3]。これは二つのベクトルの商と言っても同じである[4]。四元数をスカラーと三次元のベクトルとの和として表すこともできる。
なお、虚数単位i,j,kについても非可換であることが知られている。
現代数学の観点からは、四元数全体からなる集合は、実数体上の4次元結合的ノルム多元体であり、またそれゆえに非可換整域となる。歴史的には四元数の体系は、最初に発見された非可換多元体である[5]。四元数全体の成すこの代数は、ハミルトンに因んで H︵あるいは黒板太文字で ℍ︶と書かれる。またこの代数を、クリフォード代数 Cℓ0,2(R) ≅ Cℓ03,0(R) として定義することもできる。
この代数 Hは解析学において特別な位置を占めている。というのも、フロベニウスの定理に従えば Hは実数全体 ℝ を真の部分環として含む有限次元可除環の2種類しかないうちの一つ︵もう一つは複素数全体 ℂ︶だからである。
従って、単位四元数は三次元球面 S3上の群構造を選んだものとして考えることができて、群 Spin(3) を与える。これは 2次特殊ユニタリ群 SU(2) に同型、あるいはまた SO(3)の普遍被覆に同型である。
このとき 1, i, j, kは実数体上線型独立である。
四元数は純粋数学のみならず応用数学、特に3Dグラフィクスやコンピュータビジョンにおいて三次元での回転の計算でも用いられる。これはオイラー角や回転行列あるいはそれらに代わる道具などとともに、必要に応じて利用される。
四元数についての最初の記述は、1843年にアイルランドの数学者ウィリアム・ローワン・ハミルトンによってなされ[1][2]、3次元空間の力学に応用された。
四元数の特徴は、積について非可換であることである。ハミルトンは、四元数を三次元空間内の二つの有向直線の商として定義した[3]。これは二つのベクトルの商と言っても同じである[4]。四元数をスカラーと三次元のベクトルとの和として表すこともできる。
なお、虚数単位i,j,kについても非可換であることが知られている。
現代数学の観点からは、四元数全体からなる集合は、実数体上の4次元結合的ノルム多元体であり、またそれゆえに非可換整域となる。歴史的には四元数の体系は、最初に発見された非可換多元体である[5]。四元数全体の成すこの代数は、ハミルトンに因んで H︵あるいは黒板太文字で ℍ︶と書かれる。またこの代数を、クリフォード代数 Cℓ0,2(R) ≅ Cℓ03,0(R) として定義することもできる。
この代数 Hは解析学において特別な位置を占めている。というのも、フロベニウスの定理に従えば Hは実数全体 ℝ を真の部分環として含む有限次元可除環の2種類しかないうちの一つ︵もう一つは複素数全体 ℂ︶だからである。
従って、単位四元数は三次元球面 S3上の群構造を選んだものとして考えることができて、群 Spin(3) を与える。これは 2次特殊ユニタリ群 SU(2) に同型、あるいはまた SO(3)の普遍被覆に同型である。
 このとき 1, i, j, kは実数体上線型独立である。
四元数は純粋数学のみならず応用数学、特に3Dグラフィクスやコンピュータビジョンにおいて三次元での回転の計算でも用いられる。これはオイラー角や回転行列あるいはそれらに代わる道具などとともに、必要に応じて利用される。
四元数についての最初の記述は、1843年にアイルランドの数学者ウィリアム・ローワン・ハミルトンによってなされ[1][2]、3次元空間の力学に応用された。
四元数の特徴は、積について非可換であることである。ハミルトンは、四元数を三次元空間内の二つの有向直線の商として定義した[3]。これは二つのベクトルの商と言っても同じである[4]。四元数をスカラーと三次元のベクトルとの和として表すこともできる。
なお、虚数単位i,j,kについても非可換であることが知られている。
現代数学の観点からは、四元数全体からなる集合は、実数体上の4次元結合的ノルム多元体であり、またそれゆえに非可換整域となる。歴史的には四元数の体系は、最初に発見された非可換多元体である[5]。四元数全体の成すこの代数は、ハミルトンに因んで H︵あるいは黒板太文字で ℍ︶と書かれる。またこの代数を、クリフォード代数 Cℓ0,2(R) ≅ Cℓ03,0(R) として定義することもできる。
この代数 Hは解析学において特別な位置を占めている。というのも、フロベニウスの定理に従えば Hは実数全体 ℝ を真の部分環として含む有限次元可除環の2種類しかないうちの一つ︵もう一つは複素数全体 ℂ︶だからである。
従って、単位四元数は三次元球面 S3上の群構造を選んだものとして考えることができて、群 Spin(3) を与える。これは 2次特殊ユニタリ群 SU(2) に同型、あるいはまた SO(3)の普遍被覆に同型である。
このとき 1, i, j, kは実数体上線型独立である。
四元数は純粋数学のみならず応用数学、特に3Dグラフィクスやコンピュータビジョンにおいて三次元での回転の計算でも用いられる。これはオイラー角や回転行列あるいはそれらに代わる道具などとともに、必要に応じて利用される。
四元数についての最初の記述は、1843年にアイルランドの数学者ウィリアム・ローワン・ハミルトンによってなされ[1][2]、3次元空間の力学に応用された。
四元数の特徴は、積について非可換であることである。ハミルトンは、四元数を三次元空間内の二つの有向直線の商として定義した[3]。これは二つのベクトルの商と言っても同じである[4]。四元数をスカラーと三次元のベクトルとの和として表すこともできる。
なお、虚数単位i,j,kについても非可換であることが知られている。
現代数学の観点からは、四元数全体からなる集合は、実数体上の4次元結合的ノルム多元体であり、またそれゆえに非可換整域となる。歴史的には四元数の体系は、最初に発見された非可換多元体である[5]。四元数全体の成すこの代数は、ハミルトンに因んで H︵あるいは黒板太文字で ℍ︶と書かれる。またこの代数を、クリフォード代数 Cℓ0,2(R) ≅ Cℓ03,0(R) として定義することもできる。
この代数 Hは解析学において特別な位置を占めている。というのも、フロベニウスの定理に従えば Hは実数全体 ℝ を真の部分環として含む有限次元可除環の2種類しかないうちの一つ︵もう一つは複素数全体 ℂ︶だからである。
従って、単位四元数は三次元球面 S3上の群構造を選んだものとして考えることができて、群 Spin(3) を与える。これは 2次特殊ユニタリ群 SU(2) に同型、あるいはまた SO(3)の普遍被覆に同型である。
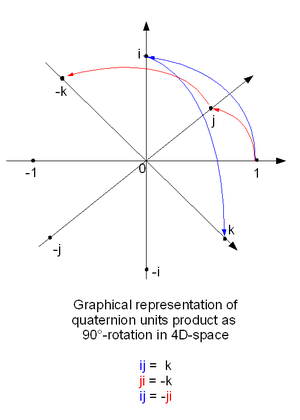
歴史
編集Here as he walked by on the 16th of October 1843 William Rowan Hamilton in a flash of genius discovered the fundamental formula for quaternion multiplication i2= j2= k2= ijk = −1 & cut it on a stone of this bridge︵1843年の10月16日、ここを通りかかったウィリアム・ローワン・ハミルトンは、天才の閃きを以って四元数の乗法の基本公式︵略︶を思いつき、この橋の石にそれを刻んだ︶ とある。 四元数の成す代数系は、1843年にウィリアム・ローワン・ハミルトンによって導入された[6]。これにはオイラーの四平方恒等式︵1748年︶やオリンデ・ロドリゲスの四つの径数を用いた一般の回転のパラメータ付け︵1840年︶などを含む重要な先駆的研究があったが、何れもその四径数回転を代数として扱ったものではなかった[7][8]。ガウスもまた1819年に四元数を発見していたのだが、そのことが公表されるのは1900年になってからのことである[9]。 ハミルトンは複素数が座標平面における点として解釈できることを知っていて、三次元空間の点に対して同じことができる方法を探していた。空間の点はそれらの座標としての数の三つ組によって表すことができ、ハミルトンはそれらの三つ組に対して加法や減法をどのようにすべきかはずっと前から分かっていたのだが、乗法と除法をどう定めるかという問題については長く行き詰ったままであった。ハミルトンは、空間における二点の座標の商をどのように計算すべきかを形にすることができなかったのである。 四元数についての大きな転換点がついに訪れたのは、1843年10月16日の月曜日、ダブリンにおいてハミルトンが理事会の長を務めることになるアイルランド王立アカデミーへの道すがら、妻とともにロイヤル運河の引き船道に沿って歩いているときであった。四元数の背景となる概念が頭の中で形になり、答えが明らかになったとき、ハミルトンは衝動を抑えられずに、四元数の基本公式を、渡っていたブルーム橋の石に刻みつけた。 次の日ハミルトンは、友人でフェロー数学者であったジョン・グレイヴスへ宛てて、彼の発見へと至る一連の道筋をしたためた書簡を記している。この書簡は後に London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, vol. xxv (1844), pp.489-95.[10]で公表されている。この中でハミルトンは、
And here there dawned on me the notion that we must admit, in some sense, a fourth dimension of space for the purpose of calculating with triples ... An electric circuit seemed to close, and a spark flashed forth.
そしてここで、三つ組を計算するという目的のために、空間の四番目の次元を我々はある意味で認めねばならないのだという考えが、私に光をもたらしたのだ… 電気回路が閉じて(つながり)、目の前に火花が散ったかのようだった。
と述べている。ハミルトンは、これらの乗法規則を備えた四つ組を quaternion と呼び、残りの人生の大半をその研究と教育にささげた。ハミルトンによる取り扱いは、四元数の代数的性質を強調する現代的なアプローチよりも幾何学的なものである。ハミルトンは "quaternionists" の学校を設立し、数々の本で四元数の普及を図った。最後にして最長の本が Elements of Quaternions︵﹃四元数原論﹄︶で800 ページにも及ぶ︵出版されたのは彼の死後少ししてからである︶。 ハミルトンの死後も弟子のテイトが四元数の振興を続けた。同時に、ダブリンでは四元数が試験の必須題目になっていた。物理学と幾何学の主題においては、今日ではベクトルを用いて記述するような空間の運動エネルギーやマクスウェルの方程式などが、まったく四元数の言葉で記述されていた。四元数やほかの超複素数系を専ら研究するプロの研究機関である四元数学会さえ存在した。 1880年代の半ばごろから、ギブス、ヘヴィサイド、ヘルムホルツらの創始したベクトル解析によって四元数は取って代わられるようになる。ベクトル解析は四元数と同じ現象を記述するために、四元数に関する文献から自由に用語法や考え方を拝借していたが、ベクトル解析の方が概念的に簡単で、記法もすっきりしていたので、遂には数学と物理学における四元数の役割は小さく追いやられることとなった。このような変遷の副作用で、現代的な読者にはハミルトンの仕事は難しく複雑なものと化してしまった。ハミルトンのオリジナルの定義は馴染みがなく、その書き振りは冗長で不明瞭である。 四元数は20世紀の後半になって、三次元の自由な回転を記述する能力を買われて、多用されることとなった。四元数による3次元の回転︵姿勢︶の表現は、3次正方行列による表現と比べて記憶容量が小さくて演算のスピードも速い。加えて、オイラー角と違ってジンバルロックが起きない。この特徴は、地上における上下方向のような絶対的な軸の無い、宇宙機のような三次元の自由度が完全にある場合の姿勢制御などでの利用に適しており[11]、宇宙機以外にもCG[12]、コンピュータビジョン、ロボット工学、制御理論、信号処理、物理学、生物情報学、分子動力学法、計算機シミュレーションおよび軌道力学など、他にも多くの応用がある。 また、四元数は二次形式との関係性により、数論からの後押しも受けている。 1989年以降、アイルランド国立大学メイヌース校の数学教室は、科学者︵2002年には物理学者のマレー・ゲルマン、2005年にスティーヴン・ワインバーグなど︶や数学者︵2003年のアンドリュー・ワイルズなど︶からなる、ダンシンク天文台からロイヤル運河の橋までを歩く巡礼の旅を開催している。ハミルトンが橋に刻みつけた公式はもはや見ることはできないが。物理学への歴史的影響
編集P.R.ジラールのエッセイ The quaternion group and modern physics[13]︵﹁四元数群と現代物理学﹂︶は、四元数の物理学における役割について論じている。それは現代代数学において "数々の物理的な共変性の群‥SO(3)、ローレンツ群、一般相対性群、クリフォード代数SU(2) および共形群などが容易く四元数群に関連付けられることを示している"。ジラールは群の表現論を議論し、結晶学に関するいくつかの空間群を表現することから始めて、続いて剛体運動の運動学、その後トーマス歳差を含む特殊相対論のローレンツ群の表現に﹁複四元数﹂(complex quaternion)︵双四元数︶を用いている。ジラールはマクスウェルの方程式を四元数変数のポテンシャル函数を用いて一本の微分方程式に表したルドヴィク・シルバースタインをはじめとする5人の著者を引いている。一般相対性を考慮してルンゲ=レンツベクトルを表し、またクリフォード代数の例としてクリフォード複四元数︵分解型双四元数︶に言及した。最後にジラールは、複四元数の逆数を使って時空の共形写像について述べている。50にも及ぶ参考文献には、アレクサンダー・マクファーレンおよび四元数学会におけるジラール自身の広報も含まれている。また、1999年にジラールはアインシュタインの一般相対性の方程式が如何にして四元数に直結するクリフォード代数を用いて定式化されるかを示している[14]。 四元数についてのより個人的な見解をジョアキム・ランベックが1995年に書いている。エッセイ If Hamilton had prevailed: quaternions in physics︵﹁もしハミルトンが勝利していたら‥物理学における四元数﹂︶には "My own interest as a graduate student was raised by the inspiring book by Silberstein"︵院生としての私の興味はシルバースタインの本に刺激を受けて生じた︶とある。ランベックは He concluded by stating "I firmly believe that quaternions can supply a shortcut for pure mathematicians who wish to familiarize themselves with certain aspects of theoretical physics."[15]︵﹁私は四元数が、理論物理学のある種の側面に習熟しようと望む純粋数学者へ、近道を与えるものと堅く信じる﹂︶と述べることによって結論を下している。 2007年、アレキサンダー・エフレモフとその共同研究者は、四元数空間幾何がヤン・ミルズ場と近しい関係にあることを示し、ダフィン・ケマー・ペティアウ方程式とクライン-ゴルドン方程式への関連性を指摘した[16]。
定義
編集
集合としては、四元数全体 Hは実数体上の4次元数ベクトル空間 ℝ4 に等しい。H には3 種類の演算︵加法、スカラー乗法、四元数の乗法︶が入る。H の二元の和は、R4 の元としての和で定義され、同様に Hの元の実数倍も R4におけるスカラー倍として定義される。H の二元の積を定めるには、まず R4の基底を決めなければならないが、その元を通例 1, i, j, kと記す。H の各元はこれら基底元の線型結合で表される。つまり
a1 + bi+ cj+ dk︵a, b, c, dは実数︶
の形に一意に表される。基底元 1は Hの乗法単位元であるため、通常省略して
a + bi+ cj+ dk
と表すのが普通である。この基底が与えられたところで、四元数の結合的乗法は、初めに基底元同士の積を定義して、一般の積はそれを分配律を用いて拡張することで定義される。
基底間の乗法
編集| × | 1 | i | j | k |
|---|---|---|---|---|
| 1 | 1 | i | j | k |
| i | i | −1 | k | −j |
| j | j | −k | −1 | i |
| k | k | j | −i | −1 |
H の基底元 i, j, kに対して等式
 は i, j, kの間の可能なすべての積を決定する。例えば
は i, j, kの間の可能なすべての積を決定する。例えば  の両辺に kを右から掛ければ
の両辺に kを右から掛ければ
 を得る。他の積も同じようにして得られて、結局
を得る。他の積も同じようにして得られて、結局
 が可能なすべての積を列挙したものとなる。これは左側の因子を列に、右側の因子を行にそれぞれ充てて、表の形にまとめることができる︵乗積表︶。
が可能なすべての積を列挙したものとなる。これは左側の因子を列に、右側の因子を行にそれぞれ充てて、表の形にまとめることができる︵乗積表︶。
 は i, j, kの間の可能なすべての積を決定する。例えば
は i, j, kの間の可能なすべての積を決定する。例えば  の両辺に kを右から掛ければ
の両辺に kを右から掛ければ
 を得る。他の積も同じようにして得られて、結局
を得る。他の積も同じようにして得られて、結局
 が可能なすべての積を列挙したものとなる。これは左側の因子を列に、右側の因子を行にそれぞれ充てて、表の形にまとめることができる︵乗積表︶。
が可能なすべての積を列挙したものとなる。これは左側の因子を列に、右側の因子を行にそれぞれ充てて、表の形にまとめることができる︵乗積表︶。
ハミルトン積
編集
二つの四元数 a1+ b1i+ c1j+ d1kと a2+ b2i+ c2j+ d2kに対し、それらのハミルトン積 (a1 + b1i+ c1j+ d1k)(a2 + b2i+ c2j+ d2k) は、基底間の積と分配律によって与えられる。具体的には、この積は分配律により基底元の積和の形に展開することができて、
 となるので、ここで先の基底元の間の乗法規則を適用して
となるので、ここで先の基底元の間の乗法規則を適用して
 を得る[6]。
を得る[6]。
 となるので、ここで先の基底元の間の乗法規則を適用して
となるので、ここで先の基底元の間の乗法規則を適用して
 を得る[6]。
を得る[6]。
順序組として
編集H の基底 1, i, j, k を用いて H を四つ組の集合
として表すことができる。このとき基底元は
であり、加法、乗法の定義式は
で与えられる。
スカラー部とベクトル部
編集
四元数 a+ bi+ cj+ dkについて、特に b= c= d= 0 であるものは実数体上のスカラーである。bi + cj+ dkで、b, c, dの内少なくとも一つが、0 でないもの (bcd ≠ 0) を純虚 (pure imaginary) という。
四元数 a+ bi+ cj+ dkに対して、a をその実部 (real part) またはスカラー部 (scalar part) といい、bi + cj+ dkをその虚部 (imagenary part) または ベクトル部 (vector part) という。四元数のスカラー部は実数であり、ベクトル部は 0 または純虚である。任意の四元数は4次元ベクトル空間のベクトルではあるけれども、ここではベクトルあるいはベクトル元という言葉を、専ら純虚四元数を指すのに用いる。この規約の下、ベクトル元ということはベクトル空間 R3の元ということと同じ意味になる。
ハミルトンは純虚四元数を right quaternion︵﹁正しい四元数﹂︶と呼び[17][18]、実︵四元︶数を scalar quaternion︵﹁スカラー四元数﹂︶と呼んだ。
四元数をスカラー部とベクトル部に分解して
 と表すと、加法、乗法の定義式は
と表すと、加法、乗法の定義式は

 となる。ここで "⋅" はベクトルのドット積、"×" はベクトルのクロス積である。特に、実部が 0 の四元数に対しては
となる。ここで "⋅" はベクトルのドット積、"×" はベクトルのクロス積である。特に、実部が 0 の四元数に対しては
 が成り立つ。
が成り立つ。
 と表すと、加法、乗法の定義式は
と表すと、加法、乗法の定義式は

 となる。ここで "⋅" はベクトルのドット積、"×" はベクトルのクロス積である。特に、実部が 0 の四元数に対しては
となる。ここで "⋅" はベクトルのドット積、"×" はベクトルのクロス積である。特に、実部が 0 の四元数に対しては
 が成り立つ。
が成り立つ。
共軛、ノルムおよび逆数
編集
四元数の共軛︵きょうやく︶は複素共役およびクリフォード代数の元の転置 (transposition) あるいは逆転 (reversal) の類似物である。四元数 q= a+ bi+ cj+ dkに対して、q の共軛は
a − bi− cj− dk
で定義される。これを q∗, q[6], qt, ~q などで表す。共軛をとる操作は対合、つまり自身を自身の逆とする変換であり、一つの元の共軛を二度とればもとの元に戻る。2つの四元数の積の共軛は、それぞれの四元数の共軛を﹁順番を逆にして﹂掛けたものになる。つまり p, qを四元数とすれば
(pq)∗ = q∗p∗
であって p∗q∗ でない。
複素数における共軛とは異なり、四元数の共軛は乗法と加法を用いて完全に書き表すことができる‥
 共軛を用いると、四元数 pの実部、虚部はそれぞれ
p + p*/2, p− p*/2
となる。
四元数 qのノルム ‖ q ‖ は、自身とその共軛の積の平方根として定義される‥
共軛を用いると、四元数 pの実部、虚部はそれぞれ
p + p*/2, p− p*/2
となる。
四元数 qのノルム ‖ q ‖ は、自身とその共軛の積の平方根として定義される‥
 ︵ハミルトンはこれを四元数のテンソルと呼んだが、この用語は現代的な意味でのテンソルと衝突する︶
これは、H を数ベクトル空間 R4と見なした時のユークリッドノルムに等しく、ノルムの公理を満たす。すなわち、常に非負の実数で、任意の2つの四元数 p, qに対して
︵ハミルトンはこれを四元数のテンソルと呼んだが、この用語は現代的な意味でのテンソルと衝突する︶
これは、H を数ベクトル空間 R4と見なした時のユークリッドノルムに等しく、ノルムの公理を満たす。すなわち、常に非負の実数で、任意の2つの四元数 p, qに対して
 が成り立つ。特に、実数 α に対して
が成り立つ。特に、実数 α に対して
 が成り立つ。
この乗法性は、積の共軛に関する式からの帰結である。あるいは、正方行列の行列式の乗法性と公式
が成り立つ。
この乗法性は、積の共軛に関する式からの帰結である。あるいは、正方行列の行列式の乗法性と公式
 ︵i は通常の虚数単位︶から乗法性を示すこともできる。
このノルムを使って、四元数 pと qの間の距離 d(p, q) を、それらの差のノルム (d(p, q) = ‖ p − q ‖) として定義することができる。これにより Hは距離空間となり、加法と乗法はこの距離位相に関して連続になる。
︵i は通常の虚数単位︶から乗法性を示すこともできる。
このノルムを使って、四元数 pと qの間の距離 d(p, q) を、それらの差のノルム (d(p, q) = ‖ p − q ‖) として定義することができる。これにより Hは距離空間となり、加法と乗法はこの距離位相に関して連続になる。
 共軛を用いると、四元数 pの実部、虚部はそれぞれ
p + p*/2, p− p*/2
となる。
四元数 qのノルム ‖ q ‖ は、自身とその共軛の積の平方根として定義される‥
共軛を用いると、四元数 pの実部、虚部はそれぞれ
p + p*/2, p− p*/2
となる。
四元数 qのノルム ‖ q ‖ は、自身とその共軛の積の平方根として定義される‥
 ︵ハミルトンはこれを四元数のテンソルと呼んだが、この用語は現代的な意味でのテンソルと衝突する︶
これは、H を数ベクトル空間 R4と見なした時のユークリッドノルムに等しく、ノルムの公理を満たす。すなわち、常に非負の実数で、任意の2つの四元数 p, qに対して
︵ハミルトンはこれを四元数のテンソルと呼んだが、この用語は現代的な意味でのテンソルと衝突する︶
これは、H を数ベクトル空間 R4と見なした時のユークリッドノルムに等しく、ノルムの公理を満たす。すなわち、常に非負の実数で、任意の2つの四元数 p, qに対して
 が成り立つ。特に、実数 α に対して
が成り立つ。特に、実数 α に対して
 が成り立つ。
この乗法性は、積の共軛に関する式からの帰結である。あるいは、正方行列の行列式の乗法性と公式
が成り立つ。
この乗法性は、積の共軛に関する式からの帰結である。あるいは、正方行列の行列式の乗法性と公式
 ︵i は通常の虚数単位︶から乗法性を示すこともできる。
このノルムを使って、四元数 pと qの間の距離 d(p, q) を、それらの差のノルム (d(p, q) = ‖ p − q ‖) として定義することができる。これにより Hは距離空間となり、加法と乗法はこの距離位相に関して連続になる。
︵i は通常の虚数単位︶から乗法性を示すこともできる。
このノルムを使って、四元数 pと qの間の距離 d(p, q) を、それらの差のノルム (d(p, q) = ‖ p − q ‖) として定義することができる。これにより Hは距離空間となり、加法と乗法はこの距離位相に関して連続になる。
単位四元数
編集詳細は「ベルソル」を参照
代数的性質
編集
四元数全体のなす集合 Hは実数体上の 4次元ベクトル空間を成す︵実数全体は 1次元、複素数全体は 2次元、八元数全体は 8次元である︶。四元数は加法と、結合的で分配的な乗法を持つが、その乗法は可換でない。従って四元数の全体 Hは実数体上の非可換結合多元環である。H には複素数体 ℂ の複製が含まれるが、H は C上の結合多元環にはならない。
四元数は除法が可能であるから、H は多元体︵乗法が可換でないことを除けば可換体と同様の構造︶である。実数体上の有限次元結合的多元体は非常に少なく、フロベニウスの定理はそれが R, C, Hのちょうど3種類であることを述べるものである。また、四元数のノルムにより四元数の全体はノルム多元環となるが、実数体上のノルム多元体もまた非常に限られ、フルヴィッツの定理はそれが R, C, H, Oの四種類︵O は八元数全体︶であることを述べる。四元数全体はまた、合成代数や単位的バナッハ環の一例でもある。
| × | 1 | i | j | k | −1 | −i | −j | −k |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | i | j | k | −1 | −i | −j | −k |
| i | i | −1 | k | −j | −i | 1 | −k | j |
| j | j | −k | −1 | i | −j | k | 1 | −i |
| k | k | j | −i | −1 | −k | −j | i | 1 |
| −1 | −1 | −i | −j | −k | 1 | i | j | k |
| −i | −i | 1 | −k | j | i | −1 | k | −j |
| −j | −j | k | 1 | −i | j | −k | −1 | i |
| −k | −k | −j | i | 1 | k | j | −i | −1 |
基底元の積は別の基底元に符号を付けたものになるから、集合 {±1, ±i, ±j, ±k} はその乗法に関して群を成す。この群は四元数群と呼ばれ、Q8 で表す[19]。Q8 の実係数群環 RQ8は環であり、また R上の 8次元ベクトル空間でもあり、Q8 の各元を基底ベクトルに持つ。四元数体 Hは RQ8を 1 + (−1), i+ (−i), j+ (−j), k+ (−k) で生成するイデアルで割った剰余環になっている。ここで、生成元となっている各差の第一項は基底元 1, i, j, kのそれぞれ一つであり、第二項は残りの基底元 −1, −i, −j, −k のそれぞれ一つであって、これらは 1, i, j, kの︵群環の加法に関する︶加法的逆元でないことに注意︵剰余環、つまり Hの中では加法逆元になる︶。
四元数と R3 の幾何
編集
四元数のベクトル部は R3のベクトルゆえ、R3 の幾何は四元数の代数構造に反映される。ベクトルに対する多くの演算は四元数を用いて定義することができるし、それによって四元数的な手法を空間ベクトルから生じる様々なものに適用することができる。例えば、電磁気学や3DCGなどにこの方法論が使える。
本節では i, j, kを Hの虚基底ベクトル[20]と R3の基底の両方の意味で用いる。i, j, kを一斉にそれぞれ −i, −j, −k に取り替えることはベクトルを加法的逆元︵マイナス︶へ写すので、ベクトルの加法的逆元をとることと四元数の共軛をとることとは同じ意味になることに注目しよう。これを以って、四元数の共軛を﹁空間反転﹂(spatial inverse) と呼ぶことがある。
2つの純虚四元数 p= b1i+ c1j+ d1k, q= b2i+ c2j+ d2kに対して、それらのドット積は
 で与えられる。これは p∗q, qp∗, pq∗, q∗p のどのスカラー部にも等しい︵これらのベクトル部は相異なることに注意︶。それゆえドット積については
で与えられる。これは p∗q, qp∗, pq∗, q∗p のどのスカラー部にも等しい︵これらのベクトル部は相異なることに注意︶。それゆえドット積については
 という等式も成り立つ。また、p と qのクロス積は基底 (i, j, k) の元の順序︵から定まる向き︶に依存して
という等式も成り立つ。また、p と qのクロス積は基底 (i, j, k) の元の順序︵から定まる向き︶に依存して
 と定義される︵符号を決めるために向きが必要であることを想起せよ︶。これは四元数としての積 pqのベクトル部に等しく、−q∗p∗ のベクトル部とも同じく等しい。ゆえに、これについても
と定義される︵符号を決めるために向きが必要であることを想起せよ︶。これは四元数としての積 pqのベクトル部に等しく、−q∗p∗ のベクトル部とも同じく等しい。ゆえに、これについても
 なる等式が成り立つ。一般に p, qが四元数︵純虚でなくてよい︶のとき、これをスカラー部とベクトル部との和
なる等式が成り立つ。一般に p, qが四元数︵純虚でなくてよい︶のとき、これをスカラー部とベクトル部との和

 に分解すれば、等式
に分解すれば、等式
 が成り立つ。これを見ると、四元数の乗法の非可換性が純虚四元数の乗法からくるものであることが分かり、また2つの四元数が可換となるための必要十分条件がそれらのベクトル部が共線となることなども分かる。
が成り立つ。これを見ると、四元数の乗法の非可換性が純虚四元数の乗法からくるものであることが分かり、また2つの四元数が可換となるための必要十分条件がそれらのベクトル部が共線となることなども分かる。
 で与えられる。これは p∗q, qp∗, pq∗, q∗p のどのスカラー部にも等しい︵これらのベクトル部は相異なることに注意︶。それゆえドット積については
で与えられる。これは p∗q, qp∗, pq∗, q∗p のどのスカラー部にも等しい︵これらのベクトル部は相異なることに注意︶。それゆえドット積については
 という等式も成り立つ。また、p と qのクロス積は基底 (i, j, k) の元の順序︵から定まる向き︶に依存して
という等式も成り立つ。また、p と qのクロス積は基底 (i, j, k) の元の順序︵から定まる向き︶に依存して
 と定義される︵符号を決めるために向きが必要であることを想起せよ︶。これは四元数としての積 pqのベクトル部に等しく、−q∗p∗ のベクトル部とも同じく等しい。ゆえに、これについても
と定義される︵符号を決めるために向きが必要であることを想起せよ︶。これは四元数としての積 pqのベクトル部に等しく、−q∗p∗ のベクトル部とも同じく等しい。ゆえに、これについても
 なる等式が成り立つ。一般に p, qが四元数︵純虚でなくてよい︶のとき、これをスカラー部とベクトル部との和
なる等式が成り立つ。一般に p, qが四元数︵純虚でなくてよい︶のとき、これをスカラー部とベクトル部との和

 に分解すれば、等式
に分解すれば、等式
 が成り立つ。これを見ると、四元数の乗法の非可換性が純虚四元数の乗法からくるものであることが分かり、また2つの四元数が可換となるための必要十分条件がそれらのベクトル部が共線となることなども分かる。
が成り立つ。これを見ると、四元数の乗法の非可換性が純虚四元数の乗法からくるものであることが分かり、また2つの四元数が可換となるための必要十分条件がそれらのベクトル部が共線となることなども分かる。
行列表現
編集
複素数の行列表現と全く同様に、四元数も行列で表現することができる。四元数を行列で表現し、四元数の加法と乗法を行列のそれに対応させる方法は、少なくとも二つあり、一つは 複素 2次正方行列を用いるもの、もう一つは実 4次正方行列を用いるものである。何れの場合も、表現は線型に関連する表現の族として与えられるもので、抽象代数学の観点からは、H からそれぞれ全行列環 M2(C) および M4(R) への単射環準同型である。
複素 2次正方行列を用いて、四元数 a+ bi+ cj+ dkは
 と表現される。この表現は以下の性質を持つ‥
●複素数 (c = d= 0) は対角行列に対応する。
●四元数のノルム︵複素数のノルム同様に、自身とその共軛との積の平方根︶は対応する行列の行列式の平方根に一致する[21]。
●四元数の共軛は、対応する行列のエルミート共軛に対応する。
●単位四元数に制限すれば、この表現は S3と SU(2) との間の同型を与える。後者の群は量子力学においてスピンを記述するのに重要である︵パウリ行列を参照︶。
実 4次正方行列を用いれば、同じ四元数は
と表現される。この表現は以下の性質を持つ‥
●複素数 (c = d= 0) は対角行列に対応する。
●四元数のノルム︵複素数のノルム同様に、自身とその共軛との積の平方根︶は対応する行列の行列式の平方根に一致する[21]。
●四元数の共軛は、対応する行列のエルミート共軛に対応する。
●単位四元数に制限すれば、この表現は S3と SU(2) との間の同型を与える。後者の群は量子力学においてスピンを記述するのに重要である︵パウリ行列を参照︶。
実 4次正方行列を用いれば、同じ四元数は

 で表される。この表現では、四元数の共軛は対応する行列の転置に対応する。また、四元数のノルムの四乗は対応する行列の行列式に等しい。複素数は、行列を 2 × 2 のブロックに分けたときの区分対角行列に対応する。
で表される。この表現では、四元数の共軛は対応する行列の転置に対応する。また、四元数のノルムの四乗は対応する行列の行列式に等しい。複素数は、行列を 2 × 2 のブロックに分けたときの区分対角行列に対応する。
 と表現される。この表現は以下の性質を持つ‥
●複素数 (c = d= 0) は対角行列に対応する。
●四元数のノルム︵複素数のノルム同様に、自身とその共軛との積の平方根︶は対応する行列の行列式の平方根に一致する[21]。
●四元数の共軛は、対応する行列のエルミート共軛に対応する。
●単位四元数に制限すれば、この表現は S3と SU(2) との間の同型を与える。後者の群は量子力学においてスピンを記述するのに重要である︵パウリ行列を参照︶。
実 4次正方行列を用いれば、同じ四元数は
と表現される。この表現は以下の性質を持つ‥
●複素数 (c = d= 0) は対角行列に対応する。
●四元数のノルム︵複素数のノルム同様に、自身とその共軛との積の平方根︶は対応する行列の行列式の平方根に一致する[21]。
●四元数の共軛は、対応する行列のエルミート共軛に対応する。
●単位四元数に制限すれば、この表現は S3と SU(2) との間の同型を与える。後者の群は量子力学においてスピンを記述するのに重要である︵パウリ行列を参照︶。
実 4次正方行列を用いれば、同じ四元数は

 で表される。この表現では、四元数の共軛は対応する行列の転置に対応する。また、四元数のノルムの四乗は対応する行列の行列式に等しい。複素数は、行列を 2 × 2 のブロックに分けたときの区分対角行列に対応する。
で表される。この表現では、四元数の共軛は対応する行列の転置に対応する。また、四元数のノルムの四乗は対応する行列の行列式に等しい。複素数は、行列を 2 × 2 のブロックに分けたときの区分対角行列に対応する。
四平方和定理
編集詳細は「ラグランジュの四平方定理」を参照
複素数の対として
編集詳細は「ケーリー=ディクソンの構成法」を参照
四元数は複素数の対として表現することができる。この側面からは、四元数は複素数全体にケーリー=ディクソン構成を適用して得られたものということになる。これは、複素数の実数の対としての構成を一般化したものである。
C2 を複素数体上の二次元ベクトル空間とし、基底 (1, j) をとる。C2 に属するベクトルは
 と表される。ここで j2= −1 および ij= −ji であるものと定めると、分配律により二つのベクトルの掛け算が定義できる。いま、積 ijを kとおくと、通常の四元数の乗法規則と同じになるので、従って上記の複素ベクトルは四元数
a + bi+ cj+ dk
に対応するものである。C2 の元を順序対として、四元数を四つ組としてそれぞれ書けば、この対応は
と表される。ここで j2= −1 および ij= −ji であるものと定めると、分配律により二つのベクトルの掛け算が定義できる。いま、積 ijを kとおくと、通常の四元数の乗法規則と同じになるので、従って上記の複素ベクトルは四元数
a + bi+ cj+ dk
に対応するものである。C2 の元を順序対として、四元数を四つ組としてそれぞれ書けば、この対応は
 となる。
となる。
 と表される。ここで j2= −1 および ij= −ji であるものと定めると、分配律により二つのベクトルの掛け算が定義できる。いま、積 ijを kとおくと、通常の四元数の乗法規則と同じになるので、従って上記の複素ベクトルは四元数
a + bi+ cj+ dk
に対応するものである。C2 の元を順序対として、四元数を四つ組としてそれぞれ書けば、この対応は
と表される。ここで j2= −1 および ij= −ji であるものと定めると、分配律により二つのベクトルの掛け算が定義できる。いま、積 ijを kとおくと、通常の四元数の乗法規則と同じになるので、従って上記の複素ベクトルは四元数
a + bi+ cj+ dk
に対応するものである。C2 の元を順序対として、四元数を四つ組としてそれぞれ書けば、この対応は
 となる。
となる。
−1 の平方根
編集
−1 の平方根は、複素数の範囲では ±i であるが、H では −1 の平方根は無数に存在する。x2 = −1 の四元数解は三次元空間内の単位球面を成すのである。これを見るのに q= a+ bi+ cj+ dkを四元数とし、その平方が −1 に等しいものと仮定する。a, b, c, dが満たすべき条件は



 である。後の3つの方程式より a= 0 または b= c= d= 0 であるが、後者は残りの方程式から a2= −1 となり、a は実数であるから不可能である。故に a= 0 ⋀ b2+ c2+ d2= 1 となる。即ち、平方が −1 になる四元数は、ノルムが 1の純虚四元数であることが分かる。定義により、このような四元数全体の成す集合は2次単位球面である。
故に、負の実四元数は無数の平方根を持つことも分かるが、それ以外の四元数の平方根はただ二つ︵0 についてはただ一つ︶である。
H における −1 の平方根のこのような同定はハミルトンが与えている[22]が、他の文献では触れられないことがよくある。1971年にサム・パーリスは −1 の平方根の成す球面について、米国数学教師評議会出版の﹁代数学における歴史的話題﹂(Historical Topics in Algebra p.39) において3ページを割いて触れている。より近くでは、イアン・ポーティアスの本﹁クリフォード代数と古典群﹂(Clifford Algebras and the Classical Groups Cambridge, 1995, proposition 8.13, p.60) にこの球面についての記述があり、また Conway & Smith (2003) のp.40には﹁任意の虚数単位を i, それに直交する虚数単位の一つを j, それらの積を k﹂("any imaginary unit may be callediTemplate:, and perpendicular onej, and their product k") として、この球面についての別な言明がある。
である。後の3つの方程式より a= 0 または b= c= d= 0 であるが、後者は残りの方程式から a2= −1 となり、a は実数であるから不可能である。故に a= 0 ⋀ b2+ c2+ d2= 1 となる。即ち、平方が −1 になる四元数は、ノルムが 1の純虚四元数であることが分かる。定義により、このような四元数全体の成す集合は2次単位球面である。
故に、負の実四元数は無数の平方根を持つことも分かるが、それ以外の四元数の平方根はただ二つ︵0 についてはただ一つ︶である。
H における −1 の平方根のこのような同定はハミルトンが与えている[22]が、他の文献では触れられないことがよくある。1971年にサム・パーリスは −1 の平方根の成す球面について、米国数学教師評議会出版の﹁代数学における歴史的話題﹂(Historical Topics in Algebra p.39) において3ページを割いて触れている。より近くでは、イアン・ポーティアスの本﹁クリフォード代数と古典群﹂(Clifford Algebras and the Classical Groups Cambridge, 1995, proposition 8.13, p.60) にこの球面についての記述があり、また Conway & Smith (2003) のp.40には﹁任意の虚数単位を i, それに直交する虚数単位の一つを j, それらの積を k﹂("any imaginary unit may be callediTemplate:, and perpendicular onej, and their product k") として、この球面についての別な言明がある。



 である。後の3つの方程式より a= 0 または b= c= d= 0 であるが、後者は残りの方程式から a2= −1 となり、a は実数であるから不可能である。故に a= 0 ⋀ b2+ c2+ d2= 1 となる。即ち、平方が −1 になる四元数は、ノルムが 1の純虚四元数であることが分かる。定義により、このような四元数全体の成す集合は2次単位球面である。
故に、負の実四元数は無数の平方根を持つことも分かるが、それ以外の四元数の平方根はただ二つ︵0 についてはただ一つ︶である。
H における −1 の平方根のこのような同定はハミルトンが与えている[22]が、他の文献では触れられないことがよくある。1971年にサム・パーリスは −1 の平方根の成す球面について、米国数学教師評議会出版の﹁代数学における歴史的話題﹂(Historical Topics in Algebra p.39) において3ページを割いて触れている。より近くでは、イアン・ポーティアスの本﹁クリフォード代数と古典群﹂(Clifford Algebras and the Classical Groups Cambridge, 1995, proposition 8.13, p.60) にこの球面についての記述があり、また Conway & Smith (2003) のp.40には﹁任意の虚数単位を i, それに直交する虚数単位の一つを j, それらの積を k﹂("any imaginary unit may be callediTemplate:, and perpendicular onej, and their product k") として、この球面についての別な言明がある。
である。後の3つの方程式より a= 0 または b= c= d= 0 であるが、後者は残りの方程式から a2= −1 となり、a は実数であるから不可能である。故に a= 0 ⋀ b2+ c2+ d2= 1 となる。即ち、平方が −1 になる四元数は、ノルムが 1の純虚四元数であることが分かる。定義により、このような四元数全体の成す集合は2次単位球面である。
故に、負の実四元数は無数の平方根を持つことも分かるが、それ以外の四元数の平方根はただ二つ︵0 についてはただ一つ︶である。
H における −1 の平方根のこのような同定はハミルトンが与えている[22]が、他の文献では触れられないことがよくある。1971年にサム・パーリスは −1 の平方根の成す球面について、米国数学教師評議会出版の﹁代数学における歴史的話題﹂(Historical Topics in Algebra p.39) において3ページを割いて触れている。より近くでは、イアン・ポーティアスの本﹁クリフォード代数と古典群﹂(Clifford Algebras and the Classical Groups Cambridge, 1995, proposition 8.13, p.60) にこの球面についての記述があり、また Conway & Smith (2003) のp.40には﹁任意の虚数単位を i, それに直交する虚数単位の一つを j, それらの積を k﹂("any imaginary unit may be callediTemplate:, and perpendicular onej, and their product k") として、この球面についての別な言明がある。
複素数平面の合併としての H
編集
−1 の平方根のどの二つをとっても、四元数の中で複素数の相異なる複製を作ることができる。 q2= −1 とすれば、そのような複製は写像
 によって決定される。抽象代数学の言葉でいえば、それぞれが Cから Hへの単射環準同型︵埋め込み︶である。q と −q に対応する埋め込みの像は集合としては同じになる。
任意の実でない四元数は Cに同型な Hの部分空間上にあることを見よう。四元数 qをスカラー部とベクトル部の和として
によって決定される。抽象代数学の言葉でいえば、それぞれが Cから Hへの単射環準同型︵埋め込み︶である。q と −q に対応する埋め込みの像は集合としては同じになる。
任意の実でない四元数は Cに同型な Hの部分空間上にあることを見よう。四元数 qをスカラー部とベクトル部の和として
 とし、さらにベクトル部をノルムとベルソルの積に分解︵極分解︶して、
とし、さらにベクトル部をノルムとベルソルの積に分解︵極分解︶して、
 と書く︵これは qs+ ‖ q ‖Uq とは異なることに注意︶。q のベクトル部のベルソル Uq→v は純虚な単位四元数ゆえ、その平方は −1 である。従ってこれから、写像
と書く︵これは qs+ ‖ q ‖Uq とは異なることに注意︶。q のベクトル部のベルソル Uq→v は純虚な単位四元数ゆえ、その平方は −1 である。従ってこれから、写像
 によって複素数の複製が得られるが、この写像の下で qは複素数 qs+ ‖ q→v ‖i の像になる。
以上から、H は実数直線を共通の交わりとして持つ無数の複素数平面の合併であることが分かる。ただし、この合併は −1 の平方根の成す球面全体を︵球面の対蹠点が同じ平面に対応することを踏まえた上で︶わたって取ったものである。
によって複素数の複製が得られるが、この写像の下で qは複素数 qs+ ‖ q→v ‖i の像になる。
以上から、H は実数直線を共通の交わりとして持つ無数の複素数平面の合併であることが分かる。ただし、この合併は −1 の平方根の成す球面全体を︵球面の対蹠点が同じ平面に対応することを踏まえた上で︶わたって取ったものである。
 によって決定される。抽象代数学の言葉でいえば、それぞれが Cから Hへの単射環準同型︵埋め込み︶である。q と −q に対応する埋め込みの像は集合としては同じになる。
任意の実でない四元数は Cに同型な Hの部分空間上にあることを見よう。四元数 qをスカラー部とベクトル部の和として
によって決定される。抽象代数学の言葉でいえば、それぞれが Cから Hへの単射環準同型︵埋め込み︶である。q と −q に対応する埋め込みの像は集合としては同じになる。
任意の実でない四元数は Cに同型な Hの部分空間上にあることを見よう。四元数 qをスカラー部とベクトル部の和として
 とし、さらにベクトル部をノルムとベルソルの積に分解︵極分解︶して、
とし、さらにベクトル部をノルムとベルソルの積に分解︵極分解︶して、
 と書く︵これは qs+ ‖ q ‖Uq とは異なることに注意︶。q のベクトル部のベルソル Uq→v は純虚な単位四元数ゆえ、その平方は −1 である。従ってこれから、写像
と書く︵これは qs+ ‖ q ‖Uq とは異なることに注意︶。q のベクトル部のベルソル Uq→v は純虚な単位四元数ゆえ、その平方は −1 である。従ってこれから、写像
 によって複素数の複製が得られるが、この写像の下で qは複素数 qs+ ‖ q→v ‖i の像になる。
以上から、H は実数直線を共通の交わりとして持つ無数の複素数平面の合併であることが分かる。ただし、この合併は −1 の平方根の成す球面全体を︵球面の対蹠点が同じ平面に対応することを踏まえた上で︶わたって取ったものである。
によって複素数の複製が得られるが、この写像の下で qは複素数 qs+ ‖ q→v ‖i の像になる。
以上から、H は実数直線を共通の交わりとして持つ無数の複素数平面の合併であることが分かる。ただし、この合併は −1 の平方根の成す球面全体を︵球面の対蹠点が同じ平面に対応することを踏まえた上で︶わたって取ったものである。
可換部分環
編集四元数を変数とする函数
編集詳細は「四元変数」を参照
複素変数の函数同様に、四元変数の函数から有効な物理モデルが得られることが示唆される。例えば、マクスウェルによるもともとの電磁場の記述には四元変数函数が用いられていた。
指数・対数・冪函数
編集三次元および四次元の回転群
編集詳細は「回転 (数学)」を参照
﹁共軛︵きょうやく︶﹂あるいは﹁共軛変換﹂という言葉は、上で述べた意味以外にも、適当な非零元 rによって元 aを rar-1 へ写す変換︵内部自己同型︶の意味にも使われる。この変換の意味で与えられた元に共軛な元の全体は、実部が等しく、かつベクトル部のノルムも等しい︵従って、共軛四元数はこの変換の意味でも共軛元である︶。
故に、非零四元数全体の成す乗法群は、純虚四元数全体の成す R3の複製の上に共軛変換によって作用する。このとき、実部が 〖cos〗θ である単位四元数による共軛変換は、虚部方向を回転の軸とする回転角 2θ の回転になる。四元数を用いる優位性としては、
(一)︵オイラー角などの場合と比べて︶非特異な表現である。
(二)行列を用いるよりも簡潔に記述できて演算のスピードも速くできる。
(三)単位四元数の対で、4次元空間の回転を表せる。
などが挙げられる。
単位四元数︵ベルソル︶の全体は三次元球面 S3を成し、また乗法に関して群を成し、3次特殊直交群︵行列式が 1の 3次直交行列全体︶〖SO〗(3,R) の二重被覆群というリー群になる︵これは上記の対応において各回転に対応する単位四元数がちょうど﹁2つ﹂あることによる︶。
詳細は「点群」を参照
︵S3 自体には標準的な群構造はないが︶ベルソルの成す部分群の像は点群であり、逆に点群の逆像はベルソル全体の成す部分群となる。有限点群の逆像は、それぞれの点群の名前に二項 (binary) を付けて呼ぶ。例えば二十面体群の逆像は二項二十面体群である。
ベルソル全体の成す群は、2次特殊ユニタリ群 〖SU〗(2) に同型である。
a, b, c, dが何れも整数となるかまたは何れも分母が2の既約分数である有理数となる四元数 a+ bi+ cj+ dk全体の成す集合を Aとする。集合 Aは環︵実は整域︶であり、また束であって、フルヴィッツ整数環と呼ばれる。この環は24個の単位四元数を持ち、それらは正24胞体︵シュレーフリ記号で {3,4,3}︶の頂点になっている。
一般化
編集詳細は「四元数環」を参照
クリフォード代数 Cℓ3,0(R) の偶部分としての四元数体
編集
幾何学的計算に対する四元数の有用性は、四元数体をクリフォード代数Cℓ3,0(R) の偶部分Cℓ+3,0(R) と同一視することによって、他の次元にも一般化することができる。これは基本基底元 σ1, σ2, σ3 から構成される結合的多重ベクトル環で、基底元は

 なる積の規則に従う。これらの基本基底元が三次元空間のベクトルを表すものとすれば、ベクトル rの単位ベクトル wに直交する平面に関する鏡映 (reflection) が
なる積の規則に従う。これらの基本基底元が三次元空間のベクトルを表すものとすれば、ベクトル rの単位ベクトル wに直交する平面に関する鏡映 (reflection) が
 で表され、二つの鏡映の合成はそれぞれの鏡映に対する平面同士のなす角の二倍の回転角をもつ回転を与えることから、
で表され、二つの鏡映の合成はそれぞれの鏡映に対する平面同士のなす角の二倍の回転角をもつ回転を与えることから、
 は σ1 と σ2 とを含む平面における 180° 回転が対応する。これは四元数の対応する公式
は σ1 と σ2 とを含む平面における 180° 回転が対応する。これは四元数の対応する公式
 とよく似ているが、実はこの二つは同一視できる。それには
とよく似ているが、実はこの二つは同一視できる。それには
 と同一視して、かつこれがハミルトンの関係式
と同一視して、かつこれがハミルトンの関係式
 を保つことを確認すればよい。この描像において、四元数はベクトルではなく二重ベクトル (bivector) に対応する︵これは一次元的な﹁向き﹂ではなくて、特定の二次元平面に付随する向きと大きさを持った量である︶。また、複素数との関係もより明らかになる。つまり、二次元ではそれぞれ σ1 と σ2 の方向を持つ二つのベクトルに対して、ただ一つの基底二重ベクトル元 σ1σ2 が存在するから、虚数単位は一つだけしかないが、ベクトルの方向が三つある三次元では、三つの二重ベクトル基底 σ1σ2, σ2σ3, σ3σ1 が存在して、三つの虚数単位を持つ。
この理由付けはさらに拡張することができて、クリフォード代数Cℓ4,0(R) においては、基本となるベクトルが相異なる四つの方向を持つから、従って平面を張る線型独立な組は六種類であり、二重ベクトル基底元は六つ存在する。このような空間において、回転子 (rotor) と呼ばれるそのような四元数の拡張を用いた回転は、斉次座標系を用いた応用において非常に有効である。しかし、三次元の場合に限っては、基底二重ベクトルの数と基底ベクトルの数が一致し、各二重ベクトルを擬ベクトルと同一視することができる。
ドルストらはこの広い設定において四元数の占める優位性を以下のように同定した[24]‥
●回転子は幾何代数において自然であり何の不思議もないし、それが含む二重鏡映の情報を容易に理解できる。
●幾何代数において、回転子とそれが作用する対象は同じ空間に属する。これにより表現を変える必要がなくなり、かつ新しいデータ構造や︵四元数に関する線型代数学を要求する︶方法を考える必要もなくなる。
●回転子はベクトル元や他の四元数だけでなく、直線や平面、円、半直線など、この代数の任意の元に普遍的に適用可能である。
●ユークリッド幾何の共形モデルにおいて、回転子はこの代数の一つの元で回転、平行移動、拡大縮小を行ることができて、任意の元に普遍的に作用する。特にこれは、四元数の場合はその軸が原点を通るものに限られるのに対して、回転子は任意の軸の周りでの回転を表現できることを意味する。
●回転子の示す変換は、特に直接的に解釈することができる。
クリフォード代数のさらに詳細な幾何学的描像は幾何代数の項を参照せよ。
を保つことを確認すればよい。この描像において、四元数はベクトルではなく二重ベクトル (bivector) に対応する︵これは一次元的な﹁向き﹂ではなくて、特定の二次元平面に付随する向きと大きさを持った量である︶。また、複素数との関係もより明らかになる。つまり、二次元ではそれぞれ σ1 と σ2 の方向を持つ二つのベクトルに対して、ただ一つの基底二重ベクトル元 σ1σ2 が存在するから、虚数単位は一つだけしかないが、ベクトルの方向が三つある三次元では、三つの二重ベクトル基底 σ1σ2, σ2σ3, σ3σ1 が存在して、三つの虚数単位を持つ。
この理由付けはさらに拡張することができて、クリフォード代数Cℓ4,0(R) においては、基本となるベクトルが相異なる四つの方向を持つから、従って平面を張る線型独立な組は六種類であり、二重ベクトル基底元は六つ存在する。このような空間において、回転子 (rotor) と呼ばれるそのような四元数の拡張を用いた回転は、斉次座標系を用いた応用において非常に有効である。しかし、三次元の場合に限っては、基底二重ベクトルの数と基底ベクトルの数が一致し、各二重ベクトルを擬ベクトルと同一視することができる。
ドルストらはこの広い設定において四元数の占める優位性を以下のように同定した[24]‥
●回転子は幾何代数において自然であり何の不思議もないし、それが含む二重鏡映の情報を容易に理解できる。
●幾何代数において、回転子とそれが作用する対象は同じ空間に属する。これにより表現を変える必要がなくなり、かつ新しいデータ構造や︵四元数に関する線型代数学を要求する︶方法を考える必要もなくなる。
●回転子はベクトル元や他の四元数だけでなく、直線や平面、円、半直線など、この代数の任意の元に普遍的に適用可能である。
●ユークリッド幾何の共形モデルにおいて、回転子はこの代数の一つの元で回転、平行移動、拡大縮小を行ることができて、任意の元に普遍的に作用する。特にこれは、四元数の場合はその軸が原点を通るものに限られるのに対して、回転子は任意の軸の周りでの回転を表現できることを意味する。
●回転子の示す変換は、特に直接的に解釈することができる。
クリフォード代数のさらに詳細な幾何学的描像は幾何代数の項を参照せよ。

 なる積の規則に従う。これらの基本基底元が三次元空間のベクトルを表すものとすれば、ベクトル rの単位ベクトル wに直交する平面に関する鏡映 (reflection) が
なる積の規則に従う。これらの基本基底元が三次元空間のベクトルを表すものとすれば、ベクトル rの単位ベクトル wに直交する平面に関する鏡映 (reflection) が
 で表され、二つの鏡映の合成はそれぞれの鏡映に対する平面同士のなす角の二倍の回転角をもつ回転を与えることから、
で表され、二つの鏡映の合成はそれぞれの鏡映に対する平面同士のなす角の二倍の回転角をもつ回転を与えることから、
 は σ1 と σ2 とを含む平面における 180° 回転が対応する。これは四元数の対応する公式
は σ1 と σ2 とを含む平面における 180° 回転が対応する。これは四元数の対応する公式
 とよく似ているが、実はこの二つは同一視できる。それには
とよく似ているが、実はこの二つは同一視できる。それには
 と同一視して、かつこれがハミルトンの関係式
と同一視して、かつこれがハミルトンの関係式
 を保つことを確認すればよい。この描像において、四元数はベクトルではなく二重ベクトル (bivector) に対応する︵これは一次元的な﹁向き﹂ではなくて、特定の二次元平面に付随する向きと大きさを持った量である︶。また、複素数との関係もより明らかになる。つまり、二次元ではそれぞれ σ1 と σ2 の方向を持つ二つのベクトルに対して、ただ一つの基底二重ベクトル元 σ1σ2 が存在するから、虚数単位は一つだけしかないが、ベクトルの方向が三つある三次元では、三つの二重ベクトル基底 σ1σ2, σ2σ3, σ3σ1 が存在して、三つの虚数単位を持つ。
この理由付けはさらに拡張することができて、クリフォード代数Cℓ4,0(R) においては、基本となるベクトルが相異なる四つの方向を持つから、従って平面を張る線型独立な組は六種類であり、二重ベクトル基底元は六つ存在する。このような空間において、回転子 (rotor) と呼ばれるそのような四元数の拡張を用いた回転は、斉次座標系を用いた応用において非常に有効である。しかし、三次元の場合に限っては、基底二重ベクトルの数と基底ベクトルの数が一致し、各二重ベクトルを擬ベクトルと同一視することができる。
ドルストらはこの広い設定において四元数の占める優位性を以下のように同定した[24]‥
●回転子は幾何代数において自然であり何の不思議もないし、それが含む二重鏡映の情報を容易に理解できる。
●幾何代数において、回転子とそれが作用する対象は同じ空間に属する。これにより表現を変える必要がなくなり、かつ新しいデータ構造や︵四元数に関する線型代数学を要求する︶方法を考える必要もなくなる。
●回転子はベクトル元や他の四元数だけでなく、直線や平面、円、半直線など、この代数の任意の元に普遍的に適用可能である。
●ユークリッド幾何の共形モデルにおいて、回転子はこの代数の一つの元で回転、平行移動、拡大縮小を行ることができて、任意の元に普遍的に作用する。特にこれは、四元数の場合はその軸が原点を通るものに限られるのに対して、回転子は任意の軸の周りでの回転を表現できることを意味する。
●回転子の示す変換は、特に直接的に解釈することができる。
クリフォード代数のさらに詳細な幾何学的描像は幾何代数の項を参照せよ。
を保つことを確認すればよい。この描像において、四元数はベクトルではなく二重ベクトル (bivector) に対応する︵これは一次元的な﹁向き﹂ではなくて、特定の二次元平面に付随する向きと大きさを持った量である︶。また、複素数との関係もより明らかになる。つまり、二次元ではそれぞれ σ1 と σ2 の方向を持つ二つのベクトルに対して、ただ一つの基底二重ベクトル元 σ1σ2 が存在するから、虚数単位は一つだけしかないが、ベクトルの方向が三つある三次元では、三つの二重ベクトル基底 σ1σ2, σ2σ3, σ3σ1 が存在して、三つの虚数単位を持つ。
この理由付けはさらに拡張することができて、クリフォード代数Cℓ4,0(R) においては、基本となるベクトルが相異なる四つの方向を持つから、従って平面を張る線型独立な組は六種類であり、二重ベクトル基底元は六つ存在する。このような空間において、回転子 (rotor) と呼ばれるそのような四元数の拡張を用いた回転は、斉次座標系を用いた応用において非常に有効である。しかし、三次元の場合に限っては、基底二重ベクトルの数と基底ベクトルの数が一致し、各二重ベクトルを擬ベクトルと同一視することができる。
ドルストらはこの広い設定において四元数の占める優位性を以下のように同定した[24]‥
●回転子は幾何代数において自然であり何の不思議もないし、それが含む二重鏡映の情報を容易に理解できる。
●幾何代数において、回転子とそれが作用する対象は同じ空間に属する。これにより表現を変える必要がなくなり、かつ新しいデータ構造や︵四元数に関する線型代数学を要求する︶方法を考える必要もなくなる。
●回転子はベクトル元や他の四元数だけでなく、直線や平面、円、半直線など、この代数の任意の元に普遍的に適用可能である。
●ユークリッド幾何の共形モデルにおいて、回転子はこの代数の一つの元で回転、平行移動、拡大縮小を行ることができて、任意の元に普遍的に作用する。特にこれは、四元数の場合はその軸が原点を通るものに限られるのに対して、回転子は任意の軸の周りでの回転を表現できることを意味する。
●回転子の示す変換は、特に直接的に解釈することができる。
クリフォード代数のさらに詳細な幾何学的描像は幾何代数の項を参照せよ。
ブラウアー群
編集「ブラウアー群」を参照
四元数体 Hは﹁本質的に﹂唯一の︵非自明な︶中心的単純環である。これは実数体上の任意の中心的単純環は Rまたは Hの何れかにブラウアー同値︵森田同値︶であるという意味である。明確に述べれば、R のブラウアー群は、R および Hをそれぞれの代表元とする二つの同値類からなる。ここで、ブラウアー群というのは中心的単純環全体の成す集合を、一方の中心的単純環が他方の中心的単純環の上の全行列環となるという同値関係で割って得られるものであった。アルティン・ウェダーバーンの定理︵のウェダーバーンの部分︶によって、任意の中心的単純環は何らかの斜体上の行列環となるから、従って四元数体が実数体上で唯一の非自明な多元体であることが分かる。
中心的単純環︵体上の環であって、それ自身が体同様に非自明な両側イデアルを持たないという意味で単純環であり、かつその中心が基礎体に一致するもの︶は、体の拡大の非可換版の類似物であり、一般の環の拡大よりも限定的である。四元数体が実数体上の︵同値を除いて︶唯一の非自明な中心的単純環であるという事実は、複素数体が実数体上の唯一の非自明な拡大体であることに比肩する。
注記
編集
(一)^ On Quaternions; or on a new System of Imaginaries in Algebra (letter to John T. Graves, dated October 17, 1843). 1843.
(二)^ Boris Abramovich Rozenfelʹd (1988). The history of non-euclidean geometry: evolution of the concept of a geometric space. Springer. p. 385
(三)^ Hamilton. Hodges and Smith. (1853). p. 60
(四)^ Hardy 1881 pg. 32. Ginn, Heath, & co.. (1881)
(五)^ Journal of Theoretics. http://www.journaloftheoretics.com/articles/3-6/qm-pub.pdf.
(六)^ abcHazewinkel & et. al. (2004, p. 12)
(七)^ ジョン・ホートン・コンウェイ; Smith, Derek Alan (2003). On quaternions and octonions: their geometry, arithmetic, and symmetry. p. 9. ISBN 1-56881-134-9
(八)^ Robert E. Bradley, Charles Edward Sandifer (2007). Leonhard Euler: life, work and legacy. p. 193. ISBN 0-444-52728-1. 著者らはヴィルヘルム・ブラシュケが1959年に唱えた﹁四元数を初めて同定したのはオイラーで、それは1748年の5月4日のゴールドバッハへ向けた書簡においてである﹂("the quaternions were first identified by L. Euler in a letter to Goldbach written on May 4, 1748,") という主張に言及し﹁この書簡においてオイラーが四元数を﹃同定した﹄というのは如何にもナンセンスで… この主張は馬鹿げている﹂("it makes no sense whatsoever to say that Euler "identified" the quaternions in this letter... this claim is absurd.") と評している。
(九)^ Simon L. Altmann (1989-12). “Hamilton, Rodrigues, and the Quaternion Scandal”. Mathematics Magazine 62(5): 306.
(十)^ Hamilton (1844, pp. 489–495)
(11)^ HAKMEM (1972) のアイテム107に "attitude of the spacecraft" が四元数でストアされている、という表現がある。
(12)^ Ken Shoemake (1985). “Animating Rotation with Quaternion Curves”. Computer Graphics 19(3): 245-254. doi:10.1145/325165.325242. Presented at SIGGRAPH '85.
﹁トゥームレイダー﹂(1996) は、四元数を利用してスムーズな3次元回転を実現した最初の販売用コンピューターゲームである。例えば、Nick Bobick's, "Rotating Objects Using Quaternions", ゲーム・ディベロッパー (雑誌)︵1998年7月︶を参照。
(13)^ Girard, P. R. The quaternion group and modern physics (1984) Eur. J. Phys. vol 5, p. 25–32. doi:10.1088/0143-0807/5/1/007
(14)^ Einstein's equations and Clifford algebra Archived 2010年12月17日, at the Wayback Machine., Advances in Applied Clifford Algebras 9 No. 2, 225-230 (1999)
(15)^ Lambek, J. If Hamilton had prevailed: quaternions in physics (1995) Math. Intelligencer, vol. 17, #4, p. 7—15. doi:10.1007/BF03024783
(16)^ A. Yefremov, F. Smarandache, V. Christianto: Yang-Mills field from quaternion space geometry, and its Klein-Gordon representation, Progress in Physics, vol. 3, July 2007, pp.42-50. Also in Florentin Smarandache (ed.): Hadron Models and Related New Energy Issues, InfoLearnQuest, 2007, ISBN 978-1-59973-042-4, pp.208-219
(17)^ ウィリアム・ローワン・ハミルトン (1866). Hamilton Elements of Quaternions article 285. p. 310
(18)^ Hardy Elements of quaternions. library.cornell.edu. p. 65
(19)^ “quaternion group”. Wolframalpha.com. 2011年2月26日閲覧。
(20)^ Vector Analysis. Gibbs-Wilson. (1901). p. 428
(21)^ Wolframalpha.com
(22)^ ハミルトン (1899). Elements of Quaternions (2nd ed.). p. 244. ISBN 1-108-00171-8
(23)^ Lce.hut.fi
(24)^ Quaternions and Geometric Algebra. Accessed 2008-09-12. See also: Leo Dorst, Daniel Fontijne, Stephen Mann, (2007), Geometric Algebra For Computer Science, Morgan Kaufmann. ISBN 0-12-369465-5
関連項目
編集参考文献
編集出版物
編集
●H.D.エビングハウス 著、成木勇夫 訳﹃数﹄ ︿下﹀、シュプリンガー・ジャパン、2004年11月。ISBN 4-431-71124-4。
●H.D.エビングハウス 著、成木勇夫 訳﹃数﹄ ︿下﹀︵新装版︶、丸善出版、2012年9月。ISBN 978-4-621-06387-3。
●J.H.コンウェイ、R.K.ガイ 著、根上生也 訳﹃数の本﹄シュプリンガー・ジャパン、2001年11月。ISBN 4-431-70770-0。
●J.H.コンウェイ、R.K.ガイ 著、根上生也 訳﹃数の本﹄丸善出版、2012年2月。ISBN 978-4-621-06207-4。
●J.H.コンウェイ、D.A.スミス 著、山田修司 訳﹃四元数と八元数 幾何,算術,そして対称性﹄培風館、2006年11月。ISBN 978-4-563-00369-2。
●今野紀雄﹃四元数﹄森北出版、2016年11月。ISBN 978-4-627-05441-7。
●堀源一郎﹃ハミルトンと四元数 人・数の体系・応用﹄海鳴社、2007年11月。ISBN 978-4-87525-243-6。
●ウィリアム・ローワン・ハミルトン (1844), “On quaternions; or on a new system of imaginaries in Algebra” (PDF), London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 25(169): 489-495, doi:10.1080/14786444408645047
●ウィリアム・ローワン・ハミルトン (1853), "Lectures on Quaternions". Royal Irish Academy.
●ウィリアム・ローワン・ハミルトン (1866) Elements of Quaternions University of Dublin Press. Edited by William Edwin Hamilton, son of the deceased author.
●ウィリアム・ローワン・ハミルトン (1899) Elements of Quaternions volume I, (1901) volume II. Edited by Charles Jasper Joly; published by Longmans, Green & Co..
●Tait, Peter Guthrie (1873), "An elementary treatise on quaternions". 2d ed., ケンブリッジ大学出版局。
●Michiel Hazewinkel, Nadiya Gubareni, Nadezhda Mikhaĭlovna Gubareni, Vladimir V. Kirichenko. Algebras, rings and modules. Volume 1. 2004. Springer, 2004. ISBN 1-4020-2690-0
●ジェームズ・クラーク・マクスウェル (1873), "A Treatise on Electricity and Magnetism". オックスフォード大学出版局。
●Tait, Peter Guthrie (1886), "Quaternion - ウェイバックマシン︵2014年8月8日アーカイブ分︶". M.A. Sec. R.S.E. Encyclopaedia Britannica, Ninth Edition, 1886, Vol. XX, pp. 160–164. (bzipped PostScript file)
●Joly, Charles Jasper (1905), "A manual of quaternions". London, Macmillan and co., limited; New York, The Macmillan company. LCCN 05036137 //r84
●Macfarlane, Alexander (1906), "Vector analysis and quaternions", 4th ed. 1st thousand. New York, J. Wiley & Sons; [etc., etc.]. LCCN es 16000048
●ブリタニカ百科事典第11版‥"Quaternions".
●Finkelstein, David, Josef M. Jauch, Samuel Schiminovich, and David Speiser (1962), "Foundations of quaternion quantum mechanics". J. Mathematical Phys. 3, pp. 207–220, MathSciNet.
●Du Val, Patrick (1964), "Homographies, quaternions, and rotations". Oxford, Clarendon Press (Oxford mathematical monographs). LCCN 64056979 //r81
●Crowe, Michael J. (1967), A History of Vector Analysis: The Evolution of the Idea of a Vectorial System, University of Notre Dame Press. Surveys the major and minor vector systems of the 19th century (Hamilton, Möbius, Bellavitis, Clifford, Grassmann, Tait, Peirce, Maxwell, Macfarlane, MacAuley, Gibbs, Heaviside).
●Altmann, Simon L. (1986), "Rotations, quaternions, and double groups". Oxford [Oxfordshire] : Clarendon Press ; New York : Oxford University Press. LCCN 85013615 ISBN 0-19-855372-2
●Altmann, Simon L. (1989), "Hamilton, Rodrigues, and the Quaternion Scandal". Mathematics Magazine. Vol. 62, No. 5. pp.291-308, Dec. 1989.
●Adler, Stephen L. (1995), "Quaternionic quantum mechanics and quantum fields". New York : Oxford University Press. International series of monographs on physics (Oxford, England) 88. LCCN 94006306 ISBN 0-19-506643-X
●Trifonov, Vladimir (1995), "A Linear Solution of the Four-Dimensionality Problem", Europhysics Letters, 32 (8) 621–626, doi:10.1209/0295-5075/32/8/001
●Ward, J. P. (1997), "Quaternions and Cayley Numbers: Algebra and Applications", Kluwer Academic Publishers. ISBN 0-7923-4513-4
●Kantor, I. L. and Solodnikov, A. S. (1989), "Hypercomplex numbers, an elementary introduction to algebras", Springer-Verlag, New York, ISBN 0-387-96980-2
●Gürlebeck, Klaus and Sprössig, Wolfgang (1997), "Quaternionic and Clifford calculus for physicists and engineers". Chichester ; New York : Wiley (Mathematical methods in practice; v. 1). LCCN 98169958 ISBN 0-471-96200-7
●Kuipers, Jack (2002), "Quaternions and Rotation Sequences: A Primer With Applications to Orbits, Aerospace, and Virtual Reality" (reprint edition), Princeton University Press. ISBN 0-691-10298-8
●ジョン・ホートン・コンウェイ, and Smith, Derek A. (2003), "On Quaternions and Octonions: Their Geometry, Arithmetic, and Symmetry", A. K. Peters, Ltd. ISBN 1-56881-134-9 (review).
●Kravchenko, Vladislav (2003), "Applied Quaternionic Analysis", Heldermann Verlag ISBN 3-88538-228-8.
●Hanson, Andrew J. (2006), "Visualizing Quaternions", Elsevier: Morgan Kaufmann; San Francisco. ISBN 0-12-088400-3
●Trifonov, Vladimir (2007), "Natural Geometry of Nonzero Quaternions", International Journal of Theoretical Physics, 46 (2) 251–257, doi:10.1007/s10773-006-9234-9
●Ernst Binz & Sonja Pods (2008) Geometry of Heisenberg Groups American Mathematical Society, Chapter 1: "The Skew Field of Quaternions" (23 pages) ISBN 978-0-8218-4495-3.
●Vince, John A. (2008), Geometric Algebra for Computer Graphics, Springer, ISBN 978-1-84628-996-5.
●For molecules that can be regarded as classical rigid bodies molecular dynamics computer simulation employs quaternions. They were first introduced for this purpose by D.J. Evans, (1977), "On the Representation of Orientation Space", Mol. Phys., vol 34, p 317.
●Zhang, Fuzhen (1997), "Quaternions and Matrices of Quaternions", Linear Algebra and its Applications, Vol. 251, pp. 21--57.
Links and monographs
編集- Matrix and Quaternion FAQ v1.21 Frequently Asked Questions
- "Geometric Tools documentation" (frame; body) includes several papers focusing on computer graphics applications of quaternions. Covers useful techniques such as spherical linear interpolation.
- Patrick-Gilles Maillot Provides free Fortran and C source code for manipulating quaternions and rotations / position in space. Also includes mathematical background on quaternions.
- "Geometric Tools source code" (frame; body) includes free C++ source code for a complete quaternion class suitable for computer graphics work, under a very liberal license.
- Doug Sweetser, Doing Physics with Quaternions
- Quaternions for Computer Graphics and Mechanics (Gernot Hoffman)
- The Physical Heritage of Sir W. R. Hamilton (PDF)
- D. R. Wilkins, Hamilton’s Research on Quaternions
- Quaternion Julia Fractals 3D Raytraced Quaternion Julia Fractals by David J. Grossman
- Quaternion Math and Conversions Great page explaining basic math with links to straight forward rotation conversion formulae.
- John H. Mathews, Bibliography for Quaternions.
- Quaternion powers on GameDev.net
- Andrew Hanson, Visualizing Quaternions home page.
- Representing Attitude with Euler Angles and Quaternions: A Reference, Technical report and Matlab toolbox summarizing all common attitude representations, with detailed equations and discussion on features of various methods.(2007年6月25日時点のアーカイブ)
- Charles F. F. Karney, Quaternions in molecular modeling, J. Mol. Graph. Mod. 25(5), 595-604 (Jan. 2007); doi:10.1016/j.jmgm.2006.04.002; E-print arxiv:0506177.
- Johan E. Mebius, A matrix-based proof of the quaternion representation theorem for four-dimensional rotations., arXiv General Mathematics 2005.
- Johan E. Mebius, Derivation of the Euler-Rodrigues formula for three-dimensional rotations from the general formula for four-dimensional rotations., arXiv General Mathematics 2007.
- NUI Maynooth Department of Mathematics, Hamilton Walk.
- OpenGL:Tutorials:Using Quaternions to represent rotation
- David Erickson, Defence Research and Development Canada (DRDC), Complete derivation of rotation matrix from unitary quaternion representation in DRDC TR 2005-228 paper. Drdc-rddc.gc.ca
- Alberto Martinez, University of Texas Department of History, "Negative Math, How Mathematical Rules Can Be Positively Bent",Utexas.edu
- D. Stahlke, Quaternions in Classical Mechanics Stahlke.org (PDF)
- Morier-Genoud, Sophie, and Valentin Ovsienko. "Well, Papa, can you multiply triplets?", arxiv.org describes how the quaternions can be made into a skew-commutative algebra graded by Z/2×Z/2×Z/2.
- Curious Quaternions by Helen Joyce hosted by John Baez.
- Luis Ibanez "Tutorial on Quaternions" Part I Part II (PDF)
ソフトウェア
編集- Quaternion Calculator [javascript], bluetulip.org
- Quaternion Calculator [Java], theworld.com
- Quaternion Toolbox for Matlab, http://sourceforge.net/projects/qtfm/
- Boost library support for Quaternions in C++, boost.org
- Mathematics of flight simulation >Turbo-PASCAL software for quaternions, Euler angles and Extended Euler angles, xs4all.nl
外部リンク
編集- 『四元数』 - コトバンク
- 四元数 - 物理のかぎしっぽ
- 『四元数と三次元空間における回転』 - 高校数学の美しい物語
- Weisstein, Eric W. "Quaternion". mathworld.wolfram.com (英語).










