集合

集合︵しゅうごう、英: set, 仏: ensemble, 独: Menge︶とは数学における概念の1つで、大雑把に言えばいくつかの﹁もの﹂からなる﹁集まり﹂である。集合を構成する個々の﹁もの﹂のことを元 (げん、英: element; 要素) という。集合は、集合論のみならず現代数学全体における最も基本的な概念の一つであり、現代数学のほとんどが集合と写像の言葉で書かれていると言ってよい。慣例的に、ある種の集合が系 (けい、英: system) や族 (ぞく、英: family) などと呼ばれることもある。実際には、これらの呼び名に本質的な違いはないが細かなニュアンスの違いを含むと考えられている。たとえば、方程式系︵﹁相互に連立する﹂方程式の集合︶、集合族︵﹁一定の規則に基づく﹂集合の集合︶、加法族︵﹁加法的な性質を持つ﹂集合族︶など。

導入[編集]

この項目には、JIS X 0213:2004 で規定されている文字︵ハートマーク、クローバーマーク、ダイヤマーク、スペードマーク︶が含まれています︵詳細︶。

集合は﹁ものの集まり﹂である^[1]。集合の元︵要素︶として、集められる対象となる﹁もの﹂は、数、文字、記号などをはじめ、どんなものでも︵当然、集合でも︶構わない。一方で、どんな﹁集まり﹂でも集合と呼んでよいわけではない。その﹁集まり﹂が集合と呼ばれるためには、対象が﹁その集まりの元であるかどうかが不確定要素なしに一意に決定できる﹂ように定義されていなければならない。例えば、ジョーカーやコマーシャルカードを除いたトランプのスート全体 {♠︵スペード︶, ♦︵ダイヤ︶, ♣︵クラブ︶, ♥︵ハート︶} やトランプの数字全体 {A, 2, 3, 4, 5, 6, 7, 8, 9, 10, J, Q, K} は集合の例である︵A,J,Q,Kは数字では無いが、多くのトランプゲームでは数字として解釈される。︶。トランプはこれらの組 {(♠, A), ..., (♠, K), (♦, A), ..., (♦, K), (♣, A), ..., (♣, K), (♥, A), ..., (♥, K)} を符牒とする、4×13=52枚のカードであるが、これもまた集合の一例である。特に、トランプはスートの集合と数字の集合との直積集合と同一視でき、﹁52﹂はこの集合の濃度を表している。また、先のスートの集合、数字の集合の濃度はそれぞれ 4, 13 である。

トランプの記号
	A	2	3	4	5	6	7	8	9	10	J	Q	K
♠	(♠,A)	(♠,2)	(♠,3)	(♠,4)	(♠,5)	(♠,6)	(♠,7)	(♠,8)	(♠,9)	(♠,10)	(♠,J)	(♠,Q)	(♠,K)
♦	(♦,A)	(♦,2)	(♦,3)	(♦,4)	(♦,5)	(♦,6)	(♦,7)	(♦,8)	(♦,9)	(♦,10)	(♦,J)	(♦,Q)	(♦,K)
♣	(♣,A)	(♣,2)	(♣,3)	(♣,4)	(♣,5)	(♣,6)	(♣,7)	(♣,8)	(♣,9)	(♣,10)	(♣,J)	(♣,Q)	(♣,K)
♥	(♥,A)	(♥,2)	(♥,3)	(♥,4)	(♥,5)	(♥,6)	(♥,7)	(♥,8)	(♥,9)	(♥,10)	(♥,J)	(♥,Q)	(♥,K)

個々の集合を表すには、しばしばラテン文字の大文字 A, B, ..., E, F, ..., M, N, ..., S, T, ..., X, Y, ... などを使う^{[注釈 1]}。集合の元はラテン小文字 a, ..., e, ..., m, ..., s, ..., x, ... とすることが多く^{[注釈 2]}、特に集合を表す大文字に対応する小文字を使う。

帰属と包含[編集]

詳細は「部分集合」、「包含関係」、「元 (数学)」、および「帰属関係」を参照

集合と元、集合と集合などの間には含んだり含まれたりといった素朴な関係を考えることができる。帰属関係対象 $a$ が集合 $A$ を構成するものの一つであるとき、﹁ $a$ は集合 $A$ に属す﹂﹁ $a$ は集合 $A$ の要素︵あるいは元︶である﹂﹁集合 $A$ は $a$ を要素として持つ﹂などといい、 $a$ ∈ $A$ あるいは $A$ ∋ $a$ と表す。包含関係 2つの集合 $A$ , $B$ について、 $A$ に属する元がすべて $B$ にも属するとき、すなわち $x$ ∈ $A$ ⇒ $x$ ∈ $B$ が $x$ の取り方に依らずに成り立つとき、﹁ $A$ は $B$ の部分集合である﹂﹁ $A$ は $B$ に集合として含まれる﹂﹁ $A$ は $A$ を包含する﹂などといい、 $A$ ⊂ $B$ または $A$ ⊆ $B$ あるいは $B$ ⊃ $A$ または $B$ ⊇ $A$ と記す。帰属関係と包含関係は異なる概念であって、混同してはならない。例えば、 $X$ ⊂ $Y$ ⊂ $Z$ ならば必ず $X$ ⊂ $Z$ であるが、 $X$ ∈ $Y$ ∈ $Z$ からは $X$ ∈ $Z$ は必ずしも導かれない。また、 $x$ ∈ $A$ ⊂ $B$ ならば $x$ ∈ $B$ であるが、 $x$ ⊂ $A$ ∈ $B$ からは $x$ ∈ $B$ を帰結することは一般にはできない。

記法[編集]

集合の記法には、おおまかに2通りの方法がある。論理的な概念として﹁内包と外延﹂というものがあるが、ほぼそれに相当するもので、その要素をすべて列挙するという方法と、その集合に含まれるのであれば必ず満たされ、含まれないのであれば必ず満たされない条件を明示するという方法である。﹁外延﹂に相当する、すべて列挙する方法では、例えば、1, 3, 5, 7, 9 からなる集合は、

\{1,3,5,7,9\}

\{1,3,5,7,9\}

と表記する。﹁内包﹂に相当する、属するために満たすべき条件を明示する方法では、例えば、10未満の正の奇数全体の集合を、 { $x$ | $x$ は10未満の正の奇数 } と表記する。一般に、条件 $P$ ( $x$ ) があったとき、それをみたす対象だけを全て集めた集合を、

{\displaystyle \{x\mid P(

\{x\mid P(x)\}

と表記する。ここでは $x$ という変数を用いているが、{ $y$ | $P$ ( $y$ )} と書いても { $a$ | $P$ ( $a$ )} と書いても構わない。set-builder notation︵en:Set-builder notation︶やset comprehension、日本語では内包表記などとも言う。前述のようにそれぞれ、論理的な概念の外延と内包に由来するものであり日本語圏では数学分野でも今もそれらの語がよく使われているが、英語圏ではそれぞれの原語であるextensionとintensionはこの分野では今はあまり見なくなっている。条件 $P$ ( $x$ ) は﹁ $x$ が $X$ の元であって、さらに条件 $Q$ ( $x$ ) を満たす﹂というような形で与えられることが多い^[注釈 3]が、このとき定まる集合を { $x$ | $x$ ∈ $X$ かつ $Q$ ( $x$ )} のように書く代わりに、しばしば簡単に

{\displaystyle \{x\in X\mid Q(

\{x\in X\mid Q(x)\}

などと略記する。集合 { $x$ ∈ $X$ | $Q$ ( $x$ )} は $X$ の部分集合となる。また、条件 $P$ ( $x$ ) が﹁条件 $Q$ ( $y$ ) を満たすようなある $y$ を用いて $x$ = $f$ ( $y$ ) と表すことができる﹂というような形のときは、集合 { $x$ | $P$ ( $x$ )} を

{\displaystyle \{f(

\{f(y)\mid Q(y)\}

のように表すこともある。要素を外延的に書きつくせないような集合、例えば自然数全体の集合を

\{0,1,2,3,\dots \}

\{0,1,2,3,\dots \}

のように書き表すこともあるが、"..." による省略部分は誤解を生じる余地があるため、このような記法はその省略された内容の意味が明らかである場合に限られる。

外延性の公理[編集]

$A$ , $B$ を任意の集合とするとき、もし任意の集合 $X$ について﹁ $X$ が

A

の要素であるならば、そのときに限り

X

は

B

の要素である﹂が成り立つならば、

A

と

B

は等しい、とする。すなわち、

\forall A\,\forall B\,(\forall X\,(X\in A\iff X\in B)\Rightarrow A=B)

\forall A\,\forall B\,(\forall X\,(X\in A\iff X\in B)\Rightarrow A=B)

である。

「外延性の公理」を参照

直感的な説明としては、たとえば、 {1, 3, 5, 7, 9} と { $x$ | $x$ は10未満の正の奇数 } は異なる表現だが、どちらも自然数 1, 3, 5, 7, 9 を要素とする集合であるので、等しい集合だとする、ということである。

特別な集合[編集]

数学では、1つも要素を持たないような集合も考える。外延性の原理によれば、このような集合はただ一つしか存在しないので、これを空集合 (英: empty set) といい ∅ で表す。∅ は任意の集合 $A$ の部分集合である。なぜなら、任意の対象 $x$ に対して $x$ ∉ ∅ より $x$ ∈ ∅ ⇒ $x$ ∈ $A$ は真だからである。空集合の他にも決まった記号によって表される集合がいくつかある。日常的には一個だけ要素を持つものは集合とは呼ばれないが、数学ではそれも集合と呼ぶ(英語のsetやフランス語のensembleも日常的な用語では空集合や一個だけの集合に対しては使われない。) ‥

●

\mathbb {N}

\mathbb {N}

は自然数全体の集合を表す。 ●

\mathbb {Z}

\mathbb {Z}

は整数全体の集合を表す。 ●

\mathbb {Q}

\mathbb {Q}

は有理数全体の集合を表す。 ●

\mathbb {R}

\mathbb {R}

は実数全体の集合を表す。 ●

\mathbb {C}

\mathbb {C}

は複素数全体の集合を表す。 ●

\mathbb {H}

\mathbb {H}

は四元数全体の集合を表す。 ●

\mathbb {U}

\mathbb {U}

はグロタンディーク宇宙を表す。

濃度[編集]

詳細は「濃度 (数学)」を参照

有限個の元からなる集合を有限集合 (ゆうげんしゅうごう、英: finite set) と呼び、集合 $A$ の元の個数を #( $A$ ), | $A$ |, card( $A$ ) などの記号で表すことが多い。有限集合でない集合を無限集合 (むげんしゅうごう、英: infinite set) という。無限集合に対しても﹁個数﹂の概念を広げて、濃度 (のうど、英: potency) 、または基数 (きすう、英: cardinal number, 英: cardinality) というものを考える。個数を数える代わりに、ある集合を使って、その元で別の集合をラベル付け (英: indexing; 添字付け) して、一対一の対応がとれるかどうかを調べるのである。そうすると有限集合の濃度はちょうど元の個数で決まるので、ちゃんと無限集合への﹁個数﹂の拡張となる概念が定まっていることが確認できる。無限集合はどれも﹁無限個﹂の元を持っているわけだが、どの無限もみな同じというわけではなく、濃度の概念ではたくさんの無限を区別して扱うことになる。たとえば、自然数と有理数が同じ濃度を持つ、自然数と実数は真に異なる濃度を持つといったような事実は数学を学ぶ者にとってよく知られた内容である。同様の事実に、平面 $R$ ²と数直線 $R$ は同じ濃度を持ち、平面を覆いつくす平面充填曲線と呼ばれる不思議な平面曲線が何種類も存在することが述べられる。より次元の高い空間でも同様で、空間を埋め尽くす空間充填曲線が構築される。異なる次元をもつ空間が同じ濃度をもつというのは、次元や濃度が一方が他方を測るようなものではない異なる尺度であることを表しているのである。

集合の演算[編集]

いくつかの集合を扱い、その関係性について論じるとき、もともと考えていた集合たちから新しい集合を作って調べるというのは有効な手段の一つである。これらの操作は、集合に対する演算と見なすことによって、集合族に関するいくつかの代数系を提供する。それらの代数系を抽象代数系と見なせば、抽象代数学の一般論を適用することでまたいくつかの概念を提供することになる。

基本的な集合演算[編集]

結び・合併・和

詳細は「合併 (集合論)」を参照

二つの集合を「くっつけ」て一緒にしてしまうことで新しい集合を取り出すことができる。加法的な集合族の基本となる演算のひとつ。和集合。

A\cup B:=\{x\mid x\in A\lor x\in B\}.

交わり・交叉・積

詳細は「交叉 (集合論)」を参照

二つの集合の共通した部分を見つけることで、新しい集合を取り出すことができる。乗法的な集合族の基本となる演算。共通部分。

A\cap B:=\{x\mid x\in A\land x\in B\}.

差・相対補

詳細は「差集合」を参照

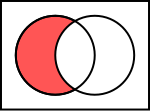
二つの集合のうちの一方の集合について、それに帰属する元のうち、同時に他方にも含まれる元を取り除いて新しい集合を作ることができる。差は一方と他方の補集合との交わりであり、乗法的な演算である。

A\smallsetminus B:=\{x\mid x\in A\land x\notin B\}.

補・絶対補

詳細は「差集合」を参照

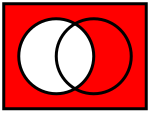
全体集合︵普遍集合︶が与えられ、任意の集合は全体集合の部分集合であるという仮定のもとで、一つの集合の全体からの差。勝手な集合はその補集合と交わりを持たず、それらの和は全体集合に一致する。

\complement A:=\{x\mid x\notin A\}.

\complement A:=\{x\mid x\notin A\}.

対称差

詳細は「対称差」を参照

二つの集合の結びに帰属する元から、その交わりに属する元を取り除いて新しい集合を考えることができる。これは結びから交わりを引いた差である。結びと同様に加法的な演算。

A\,\triangle \,B:=(A\smallsetminus B)\cup (B\smallsetminus A).

指示関数はこれらの集合演算を 0 と 1 からなる世界の代数的な演算に置き換える手段を与える。

A\leftrightarrow \mathbf {1} _{A}(x):={\begin{cases}1&(x\in A)\\0&(x\notin A)\end{cases}}.

その他の演算[編集]

もとの全体集合の中に演算結果を求めるのではなく、むしろ引数となる集合たちをもとに新しい集合を作り出すことを目的とする演算もある。

冪

詳細は「冪集合」を参照

与えられた集合に対して、その冪集合とは与えられた集合に包含される集合全体の集合である。ある集合の冪集合はその集合の部分集合からなる集合族のなかで最大のものであると言っても同じである。

{\mathcal {P}}(X):=\{S\mid S\subseteq X\}.

直積

詳細は「直積集合」を参照

二つの集合に対し、それぞれに帰属する元の順序対を要素とする集合を作ることができる。

X\times Y:=\{(x,y)\mid x\in X\land y\in Y\}.

直和・非交和

詳細は「非交和」を参照

二つの集合の、交わりを持たない和。

配置集合・写像空間

詳細は「配置集合」を参照

ある集合から別の集合への写像を一つの元と見なすならば、その全体として新たな集合が見出される。直積集合は、順序数の各元に任意の集合を対応させる写像からなる配置集合と見ることもできる。

Y^{X}:=\{f\mid f{\text{ is a mapping from }}X{\text{ to }}Y\}.

商

詳細は「商集合」を参照

集合に同値関係を与えるとき、各類をその要素とする集合を考えることができる。

{\displaystyle X/{\sim }{}:=\{[

X/{\sim }{}:=\{[x]\mid x\in X\},{\text{ where }}[x]:=\{y\in X\mid y\sim x\}.

いくつかの集合族[編集]

集合からなる族

A

を考える。

A

が集合演算についていくつかの性質を満たすとき、それらには特別の名前が与えられることがある。 ●

A

が︵有限︶交叉について閉じているとき π-系︵英語版︶であるといい、π-系が空集合を含むとき乗法族である^[2]という^[注釈^4]︵ディンキン族も参照︶。さらに可算交叉について閉じているとき δ-乗法族であるという。また、乗法族が包含関係を持つ任意の二つの集合に対し、一方から有限回の非交和を行って他方へ達する列を持つとき集合半環という。 ●

A

が︵有限︶和と︵有限︶交叉について閉じているとき、集合の束あるいは集合環という。

A

が空集合でなく︵あるいは空集合を元として含み︶、和と差について閉じている︵あるいは同じことだが対称差と交叉について閉じている︶場合に限って集合環と呼ぶ場合もある。さらに可算交叉について閉じていれば δ-集合環、可算和について閉じていれば σ-集合環という。また、これらが全体集合を含むならば代数あるいは体という。δ-集合体は σ-集合体である。 ●

A

が空集合を含み、︵有限︶和および補について閉じているとき加法族、特に有限加法族であるという。さらに可算和について閉じているならば完全加法族という。集合族

A

が加法族であることは集合体であることと等価であり、同様に完全加法族は σ-集合体の別名である。 ●単調族は包含関係に関する単調列の極限について閉じている集合族 ●ディンキン族︵d-族、δ-族︶は全体集合を含み、包含関係を持つ集合同士の差について閉じていて、可算増大列の極限について閉じている。λ-系は全体集合を含み、補について閉じていて、可算非交和について閉じている。この二つは同じ概念を定める。 ●ラミナ族はそれに属する任意の集合

A, B

が

A \subset B

または

A \supset B

または

A \cap B \neq \emptyset

の何れか一つのみを満たす。 ●ブール代数

脚注[編集]

[脚注の使い方]

注釈[編集]

(一)^ 定数や変数に対する慣例を踏襲して A, B, ... や X, Y, ... が使われるほか、英語の set, ドイツ語の Menge, フランス語の ensemble の頭文字 S, M, Eやその周辺の文字がよく使われる。 (二)^ ラテンアルファベット以外にもギリシャ文字を使うこともある。集合の集合を考えるときは、元である集合に大文字を使うことから、筆記体

\scriptstyle {\mathcal {A,\ldots ,E,\ldots ,M,\ldots ,S,\ldots ,X,\ldots }}

\scriptstyle {\mathcal {A,\ldots ,E,\ldots ,M,\ldots ,S,\ldots ,X,\ldots }}

やドイツ文字

\scriptstyle {\mathfrak {A,\ldots ,M,\ldots ,X,\ldots }}

\scriptstyle {\mathfrak {A,\ldots ,M,\ldots ,X,\ldots }}

で記したりする。このような入れ子構造は何重にも複雑な形で現われたり、同じものが違った見方をされたりするので、このような文字種の変更を行わないこともよくある。 (三)^ ﹁ $x$ が $X$ の元であって﹂というような断り書きをしない場合にも、実際には﹁普遍集合﹂ (英: universal set) あるいは﹁宇宙﹂ (英: universe) と呼ばれる、必要な議論を展開することができる程度に十分大きな集合を考え、集合と言えば必ずその普遍集合の部分集合だけを考えているといったようなことがしばしば行われる。条件 $P$ ( $x$ ) の形から $x$ の属するべき集合 $X$ がある程度限定される場合にも、断り書きはしばしば省略される。 (四)^ しばしば π-系と乗法族はこれと逆に扱われたり同義語の場合もある。例えば定義 1.3.6.や[1]は乗法族 (multiplicative class) に交叉について閉じていることのみを課している。

出典[編集]

^ 集合・位相入門. 岩波書店. (1968年6月10日)
^ 例えば定義 2.1.

外部リンク[編集]

Hazewinkel, Michiel, ed. (2001), “Set”, Encyclopedia of Mathematics, Springer, ISBN 978-1-55608-010-4
Weisstein, Eric W. "Set". mathworld.wolfram.com (英語).
set - PlanetMath.（英語）
Sets in nLab

[1] 集合・位相入門. 岩波書店. (1968年6月10日)

[5] 例えば定義 2.1.

[1]

[注釈 1]

[注釈 2]

[注釈 3]

[2]

[注釈